机器学习之分类:ROC 和曲线下面积
ROC 曲线
ROC 曲线 (接收者操作特征曲线)是一种显示分类模型在所有分类阈值下的效果的图表。该曲线绘制了以下两个参数:
- 真正利率
- 假正利率
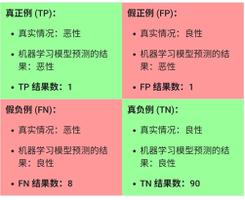
真正利率(TPR)是召回率的同义词,因此定义如下:
TPR = \dfrac{TP}{TP + FN}
假正例率(FPR)的定义如下:
FPR = \dfrac{FR}{FP + TN}
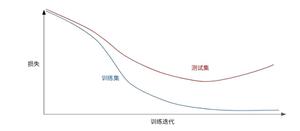
ROC 曲线用于绘制采用不同分类阈值时的 TPR 与 FPR 。降低分类阈值会导致将更多样本归为正类别,从而增加假正例和真正例的个数。下图显示了一个典型的 ROC 曲线。
图 4.不同分类阈值下的 TP 率与 FP 率
为了计算 ROC 曲线上的点,我们可以使用不同的分类阈值多次评估逻辑回归模型,但这样做效率非常低。幸运的是,有一种基于排序的高效算法可以为我们提供此类信息,这种算法称为曲线下面积。
曲线下面积:ROC 曲线下面积
曲线下面积表示“ROC 曲线下面积”。也就是说,曲线下面积测量的是从(0,0)到(1,1)之间整个二维面积(参考积分学)。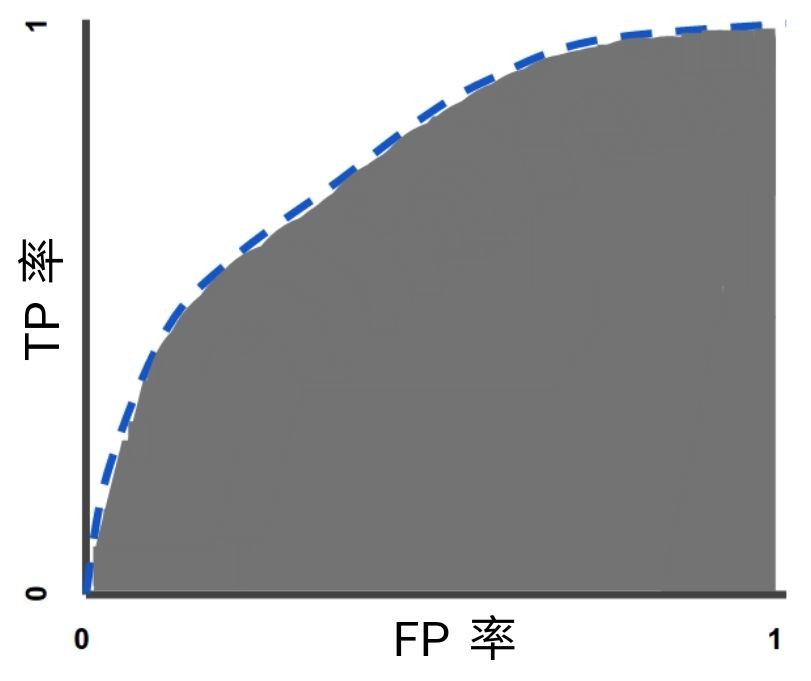
图 5.曲线下面积(ROC 曲线下面积)
曲线下面积对所有可能的分类阈值的效果进行综合衡量。曲线下面积的一种解决方式是看作模型将某个随机正类别样本排列在某个随机负泪别样本之上的概率。以下面的样本为例,逻辑回归预测从左到右以升序排列:
图 6.预测按逻辑回归分数以升序排列。
曲线下面积表示随机正类别(绿色)样本位于负类别(红色)样本右侧的概率。
曲线下面积的取值范围为 0—1 。预测结果 100%错误的模型的曲线下面积为 0.0;而预测结果 100%正确的模型的曲线下面积为 1.0。
曲线下面积因以下两个原因而比较实用:
- 曲线下面积的尺度不变。它测量预测的排名情况,而不是测量其绝对值。
- 曲线下面积的分类阈值不变。它测量预测的排名情况,而不考虑所选的分类阈值。
不过,这两个原因都有各自的局限性,这可能会导致曲线下面积在某些用例中不太实用: - 并非总是希望尺度不变。例如,有时我们非常需要被良好校准的概率输出,而曲线下面积无法告诉我们这一结果。
- 并非总是希望分类阈值不变。在假负例与假正例的代价存在较大差异的情况下,尽量减少一种类型的分类错误可能至关重要。例如,在进行垃圾邮件检测时,您可能希望优先考虑尽量减少假正例(即使这会导致假负例大幅增加)。对于此类优化,曲线下面积并非一个实用的指标。
以上是 机器学习之分类:ROC 和曲线下面积 的全部内容, 来源链接: utcz.com/p/216975.html