机器学习之支持向量机的超平面
支持向量机(Support Vector Machine)" class="reference-link">支持向量机(Support Vector Machine)
给定训练样本集 D = {(x_1,y_1), (x_2,y_2),…, (x_m,y_m)}, y_i\in{-1,+1}, 分类学习最基本的想法就是基于训练集 D 在样本空间中找到一个划分超平面,将不同类别的样本分开,但能将训练样本分开的划分超平面可能有很多,如图 6.1 所示,我们应该找哪个呢?
我们应该定义一个性能指标,然后计算在每条线上该性能指标的值,算出的值最大的那条线便是最适合的。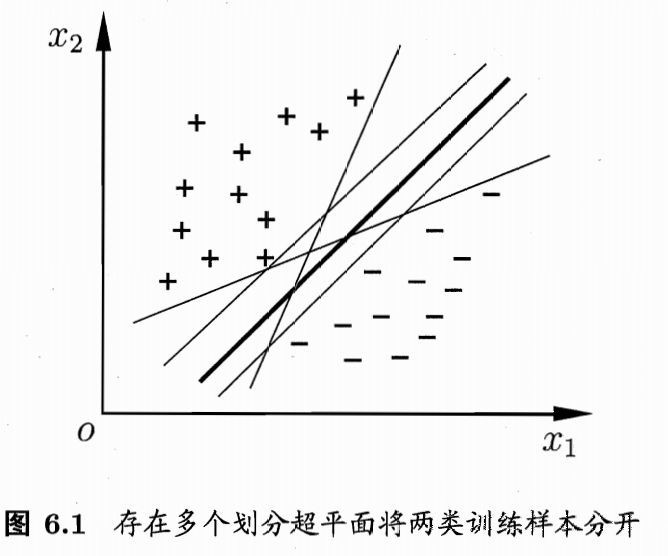
直观看上去,应该去找位于两个训练样本“正中间”的划分超平面,因为该划分超平面对训练样本局部扰动的“容忍”性最好,即对未见示例的划分能力最强。
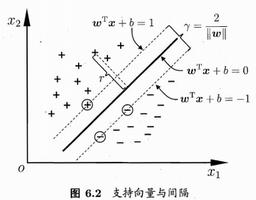
在样本空间中,划分超平面可通过如下线性方程来描述:
\mathbf{w}^T\mathbf{x}+ b = 0
其中 w = (w_1;w_2;…;w_d) 为法向量,决定了超平面的方向;b 为位移项,决定了超平面与原点之间的距离。显然,划分超平面可被法向量 w 和位移 b 确定
注意:x 向量与 w 向量维数相同
以上是 机器学习之支持向量机的超平面 的全部内容, 来源链接: utcz.com/p/217000.html