机器学习4决策树

Z时代
2024-01-10
分类：综合

机器学习-4-决策树[Python基础]

简介

　　　　决策树是基于树结构进行决策的，决策树的目的是产生一颗泛化能力强，即处理未见示例能力强的决策树，其基本流程遵循简单而直观的“分而治之”（divide-and-conquer）的策略。

伪代码

　　　　----------------------------------------

　　　　输入：训练集D = {(x₁,y₁),(x₂,y₂),........,(x_m,y_m)};

　　　　　　　属性集A = {a₁,a₂,.............,a_d}

　　　　过程：函数TreeGenerate(D,A)

　　　　　　　1：生成结点 node；

　　　　　　　2：if D中样本全属于同一类别C then

　　　　　　　3：　　将node标记为C类叶节点；return

　　　　　　　4：end if

　　　　　　　5：if A == Φ　or D中样本在A上取值相同 then

　　　　　　　6：　　将node标记为叶节点，其类别标记为D中样本数最多的类；return

　　　　　　　7：end if

　　　　　　　8：从A中选择最优划分属性a_*； #这里就需要划分算法

　　　　　　　9：for a_* 的每一个值 a_*^vdo

　　　　　　10 ：　　为node生成一个分支；令D_v表示D中在a_*上取值为a_*^v 的样本子集；

　　　　　　11 ：　　if D_v为空 then

　　　　　　12 ：　　　　将分支节点标记为叶节点，其类别标记为D中样本最多的类；return

　　　　　　13 ：　　else

　　　　　　14 ：　　　　以 TreeGenerate(D_v, A{a_*})为分支节点 #精髓递归

　　　　　　15 ：　　end if

　　　　　　16 ：end for

　　　　输出：以node为根结点的一颗决策树

　　　　--------------------------------------　

　　　　伪代码注意点

　　　　　　递归返回情况：

　　　　　　1.当前节点包含的样本全属于同一类别，无需划分；

　　　　　　2.当前属性集为空，或是所有样本在所有属性上的取值相同；

　　　　　　3.当前节点包含的样本集合为空，不能划分；

　　　　　　特别地，在第2种情形下，我们把当前节点标记为叶结点，并将其类别设定为该结点所含样本最多的类别；在第3种情形下，同样把当前结点标记为叶结点，但将其类别设定为其父结点所含样本最多的类别。即2为当前结点的后验分布，3则是把父结点的样本分布当作结点的先验分布。

划分算法

　　　　1.信息熵（information entropy）是度量样本集合纯度最常用的一种指标。假定当前样本集合D种第k类样本所占的比例为p_k(k = 1,2,........,|y|),则D的信息熵定义为

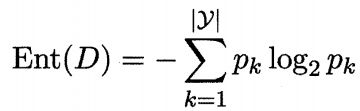
Ent（D）的值越小，则D的纯度越高。

　　　　2.信息增益（information gain）

　　　　　　假定离散属性a有V个可能的取值{a¹,a²,.......,a^v},若使用a来对样本集D进行划分，则会产生V个分支结点，其中第v个分支结点包含了D中所有在属性a上取值为av的样本，记为Dv.根据上述公式计算Dv的信息熵，再考虑到不同的分支结点包含的样本数不同，给分支结点赋予权重|Dv|/|D|，即样本数越多的分支结点的影响越大，于是可计算出用属性a对样本集D进行划分所获得的“信息增益“

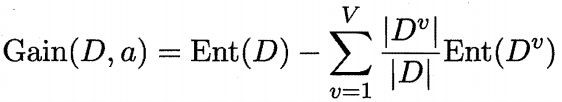
一般而言，信息增益越大，则意味着使用属性a来进行划分所获得的”纯度提升“越大。

　　　　3.增益率

　　　　　　信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，著名的C4.5决策树算法不直接使用信息增益，而是使用增益率（gain ratio）来选择最优划分属性。

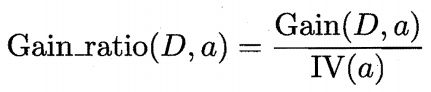
其中

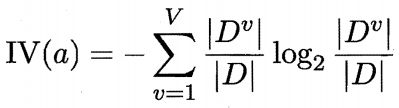
称为属性a的“固有值”。属性a的可能取值数目越多（即V越大），则IV（a）的值通常会越大。

　　　　　　需注意的是，增益率准则对可取值数目较少的属性有所偏好，因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

　　　　4.基尼指数

　　　　　　CART决策树使用“基尼系数”来选择划分属性。数据集D的纯度可以用基尼值来度量：

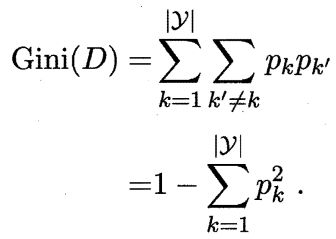
　　　　　　直观来说，Gini（D）反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此，Gini（D）越小，则数据集D的纯度越高。则属性a的基尼指数定义为

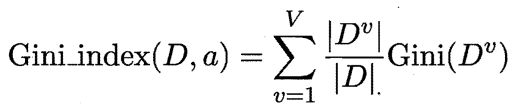
于是，我们再候选属性集合A中，选择那个使得划分后基尼指数最小的属性作为最优划分属性，即a_*= arg min Gini_index( D,a)

剪枝处理

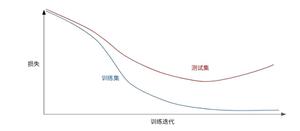
　　　　剪枝（pruning）是决策树学习算法对付“过拟合”的主要手段。

　　　　预剪枝：在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能的提升，则停止划分并将当前结点标记为叶节点；

　　　　后剪枝：从训练集生成一颗完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶节点能带来决策树泛化性能提升，则将该子树替换为叶节点。

连续与缺失值

　　　　可以将连续属性离散化，最简单的策略是采用二分法对连续属性进行处理。

　　　　缺失值处理

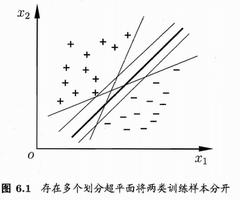
多变量决策树

　　　　emmmmm

实例代码

from math import log
import pandas as pd
import numpy as np
from matplotlib.font_manager import FontProperties
"""
函数说明：计算信息熵函数
输入：data,计算列名
输出：信息熵
"""
def compute_infoentropy(Dataframe,columns_name):
    data = Dataframe[columns_name]
    data_classify = []
    length = len(data)
for singledata in data:
if len(data_classify) == 0:
            data_classify.append([singledata,1])
else:
            exist = 0
for i in range(len(data_classify)):
if data_classify[i][0] == singledata:
                    data_classify[i][1] = data_classify[i][1]+1
                    exist = 1
if exist == 0:
                data_classify.append([singledata,1])
    infoentropy = 0
for data_classfy1 in data_classify:
        infoentropy += data_classfy1[1] / length * log(data_classfy1[1] / length,2)
    infoentropy = -infoentropy
return infoentropy
"""
函数说明：将数据依照某种类型分类
输入：数据，数据分类类型
输出：分类数据
"""
def my_classify(Dataframe,columns_name):
    data = Dataframe[columns_name]
    classify = []
for singledata in data:
if singledata notin classify:
            classify.append(singledata)
return classify
"""
函数说明：计算各类别的信息增益（information gain），并选择信息增益最大的类别，进行相应划分
输入:数据，类别
输出:最大类别
"""
def choose_bestfeature(Dataframe):
#获取columns_names
    columns_names = list(Dataframe)
    key_name = columns_names[-1]
    columns_names = columns_names[:-1]
    data_count = Dataframe[key_name].count()
    gain_list=[]
#计算各属性信息增益值
    key_infoentropy = compute_infoentropy(Dataframe,key_name)
for singlename in columns_names:
        classify = my_classify(Dataframe,singlename)
        dflist = []
for edata in classify:
            dflist.append(Dataframe[Dataframe[singlename] == edata])
        sum_infoentropy = 0
for dflist1 in dflist:
            sum_infoentropy += dflist1[key_name].count()/data_count*compute_infoentropy(dflist1,key_name)
        gain_list.append([singlename,key_infoentropy-sum_infoentropy])
    max_gain = ["",0]
for gain in gain_list:
if gain[1]>max_gain[1]:
            max_gain=gain
return max_gain[0]
"""
函数说明：获取当前最大分类的属性
输入：data
输出：特征属性数量占多数的属性
"""
def get_maxproperty(Dataframe):
    my_property = []
    clnname=list(Dataframe)
for data in Dataframe[clnname[0]]:
        exist = 0
for i in range(len(my_property)):
if my_property[i][0] == data:
                my_property[i][1] += 1
                exist = 1
if exist == 0:
            my_property.append([data,1])
    max_p=["",0]
for my_property1 in my_property:
if my_property1[1]>max_p[1]:
            max_p[0]=my_property1[0]
return max_p[0]
"""
函数说明：决策树主函数
输入：数据集
输出：字典形式的决策树
"""
def mydescion_tree(Dataframe,feature):
    key_featlist = Dataframe.iloc[:,-1]
if key_featlist.loc[key_featlist == key_featlist.iloc[0]].count() == key_featlist.count():         #如果分类相同，则取该分类
return key_featlist.iloc[0]
if Dataframe.shape[1] == 1:                                                                        #如果只剩下一列数据（即分到了最后一类特征），那么取分类占多数的分类
return get_maxproperty(Dataframe)
    bestfeature = choose_bestfeature(Dataframe)                                                        #找出当前最佳特征
    feature.append(bestfeature)
    tree = {bestfeature : {}}                                                                          #创建节点用的
    classify = my_classify(Dataframe,bestfeature)                                                      #找出当前最佳特征共有几种属性
for classify1 in classify:                                                                         #遍历当前特征的属性
# 递归，后面dataframe是获取特征等于当前属性的dataframe后并删除当前最佳特征，因为已经分过类了，进入递归。
        tree[bestfeature][classify1] = mydescion_tree(Dataframe[Dataframe[bestfeature]==classify1].drop([bestfeature],axis=1),feature)
return tree
#测试数据
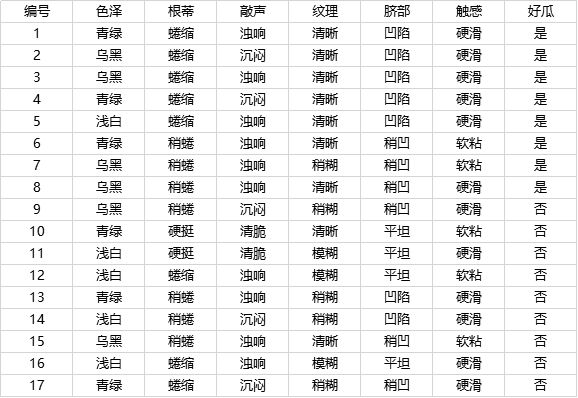
df1 = pd.read_excel("西瓜数据.xlsx",engine="openpyxl")
df1 = df1.iloc[:,1:]
tree = mydescion_tree(df1,feature=[])
print(tree)

后面还有一些补充的，未完待续。。。。

以上是机器学习4决策树的全部内容，来源链接： utcz.com/z/537758.html

机器学习4决策树

其他人也看了：