机器学习之特征工程

Z时代
2024-01-10
分类：IT

传统编程的关注点是代码. 在机器学习项目中, 关注点变成了特征表示.也就是说, 开发者通过添加和改善特征来调整模型.

将原始数据映射到特征

图 1 左侧表示来自输入数据源的原始数据, 右侧表示特征矢量, 也就是组成数据集中样本的浮点值集.特征工程指的是将原始数据转换为特征矢量.进行特征工程预计需要大量时间.
许多机器学习模型都必须将特征表示为实数向量, 因为特征值必须与模型权重相乘.

图 1. 特征工程将原始数据映射到机器学习特征

映射数值

整数和浮点数不需要特殊编码, 因为它们可以与数字权重相乘.如图 2 所示, 将原始整数值 6 转化为特征值 6.0 并没有多大的意义:

图 2. 将整数值映射到浮点值

映射分类值

分类特征具有一组离散的可能值.例如, 可能有一个名为 street_name 的特征, 其中的选项包括:

{'Charleston Road','North Shoreline Boulevard','Shorebird Way','Rengstorff Avenue'}

由于模型不能将字符串与学到的权重相乘, 因此我们使用特征工程将字符串转换为数字值.
要实现这一点, 我们可以定义一个从特征值 ( 我们将其称为可能值的词汇表 ) 到整数的映射.世界上的每条街道并非都会出现在我们的数据集中, 因此我们可以将所有其他街道分组为一个全部包罗的 “其他”类别, 称为 OOV ( 词汇表外 ) 分桶
通过这种方法, 我们可以按照以下方式将街道名映射到数字:

将 Charleston Road 映射到 0
将 North Shoreline Boulevard 映射到 1
将 Shorebird Way 映射到 2
将 Rengstorff Avenue 映射到 3
将所有其他街道 ( OOV ) 映射到 4
不过, 如果我们将这些索引数字直接纳入到模型中, 将会造成一些可能存在问题的限制:
我们将学习适用于所有街道的单一权重.例如, 如果我们学习到 street_name 的权重为 6 , 那么对于 Charleston Road , 我们会将其乘以 0 , 对于 North Shoreline Boulevard 则乘以 1 , 对于 Shorebird Way 则乘以 2 , 依次类推.以某个使用 street_name 作为特征来预测房价的模型为例.根据街道名称对房价进行线性调整的可能性不大, 此外, 这会假设您已根据平均房价对街道进行排序.我们的模型需要灵活地为每条街道学习不同的权重, 这些权重将添加到利用其他特征估算的房价中.
我们没有将 Street_name 可能有多个值的情况考虑在内.例如, 许多房屋位于两条接到的拐角处, 因此如果模型包括单个索引, 则无法在 street_name 值中对该信息进行编码.
要去除这两个限制, 我们可以为模型中的每个分类特征创建一个二元向量来表示这些值, 如下所述:
对于适用于样本的值, 将相应的向量元素设为 1
将所有其他元素设为 0
该向量的长度等于词汇表中的元素数. 当只有一个值为 1 时, 这种表示法称为独热编码; 当有多个值为 1 时, 这种表示方法称为多热编码
图 3 所示为街道 Shorebird Way 的独热编码.在此二元矢量中, 代表 Shorebird Way 的元素的值为 0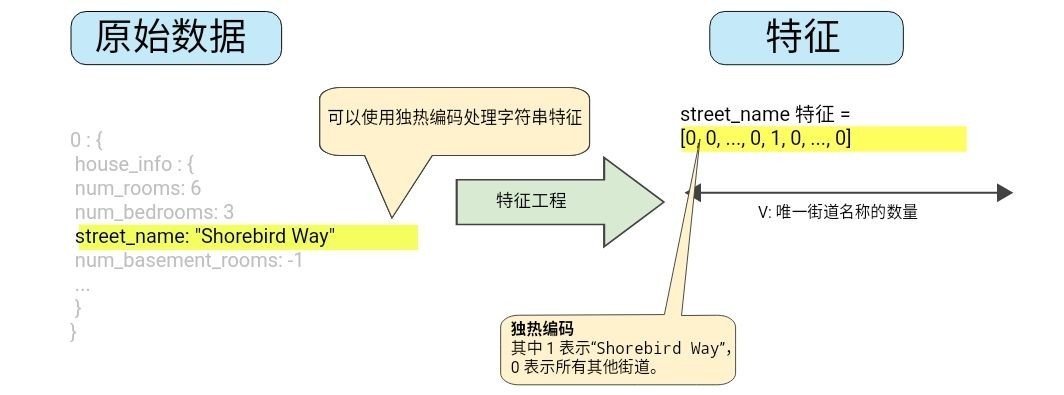
图 3. 通过独热编码映射街道地址
该方法能够有效地为每个特征值 ( 例如, 街道名称 ) 创建布尔变量.采用这种方法时, 如果房屋位于 Shorebird Way 街道上, 则只有 Shorebird Way 的二元值为 1.因此, 该模型仅使用 Shorebird Way 的权重.
同样, 如果房屋位于两条街道的拐角处, 则将两个二元值设为 1 ,并且模型将使用他们各自的权重.
注:独热编码会扩展到您不希望直接与权重相乘的数字数据, 例如邮政编码.
稀疏表示法
假设数据集中有 100 万个不同的街道名称, 您希望将其包含为 street_name 的值.如果直接创建一个包含 100 万个元素的二元向量, 其中只有 1 或 2 个元素为 true , 则是一种非常低效的表示法, 在处理向量时会占用大量的存储空间并耗费很长的计算时间.在这种情况下, 一种常用的方法是使用稀疏表示法, 其中仅存储非零值. 在稀疏表示法中, 仍然为每个特征值学习独立的模型权重, 如上所述.