【Python】统计科学之分析遇到非正态数据该怎么办?
统计科学之分析遇到非正态数据该怎么办?
张俊红发布于 今天 06:44
我们在前面讲过数据的正态性检验,介绍了检验数据是否正态的两种方法。这一节我们来看一下,如果数据不满足正态时该怎么办,答案就是将非正态数据通过Box-Cox变换进一步转换成符合正态分布的数据。这一篇就给大家分享下Box-Cox变换的具体内容。
Box-Cox变换是多种变换的总称,具体的公式如下: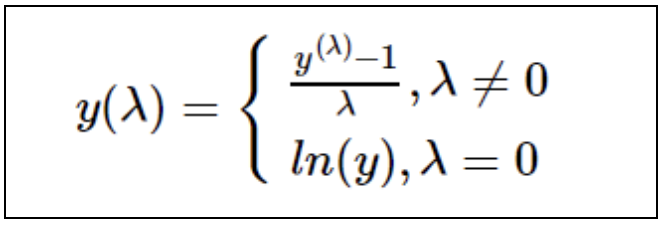
上面公式中y(λ)表示变换后的值,根据λ的值不同,属于不同的变换,当λ值取以下特定的几个值时就变成了特殊的数据变换:
- 当λ=0时,Box-Cox变换就变成了对数变换,y(λ) = ln(y);
- 当λ=0.5时,Box-Cox变换就变成了平方根变换,y(λ) = y^1/2
- 当λ=1时,Box-Cox变换变换就是它本身,y(λ) = y
- 当λ=2时,Box-Cox变换就变成了平方变化,y(λ) = y^2
- 当λ=-1时,Box-Cox变换就变成了倒数变化,y(λ) = 1/y。
λ值除了可以选择上述特定的值以外,还可以选择其他值,那当我们拿到一份非正态数据时,我们应该取λ值等于多少对齐进行变换呢?这个又该怎么定呢?
λ值取多少,我们可以利用Python中现成的函数,让函数自动去探索,然后返回给我们最优的值是多少就可以。这个函数就是boxcox_normmax,这个函数用来计算给定的非正态数据对应的最优λ值。
boxcox_normmax(x[, brack, method])参数:
x:非正态数据
brack: λ值搜索间隔,默认即可
method:计算λ值的方法,有pearsonr、mle、all三种可选,默认为pearsonr,即按照相关性的方法去计算,如果选all,则会返回各种方法的计算结果
返回值:
返回λ值
当我们得到最优的λ值以后,就可以根据λ值进行数据转换了,这个时候可以用另外的一个函数boxcox,这个函数是根据指定的λ值对原始数据进行转换。
boxcox(x[, lmbda, alpha])参数:
x:非正态数据
lambda:转换的λ值
alpha:计算置信区间时所用到的alpha值
返回值:
boxcox:经过转换以后的数据
maxlog:如果在传入时lambda参数值没有指定的话,该函数也会计算一个λ值出来
(min_ci, max_ci):如果lambda参数为空且alpha参数不为空时,会计算maxlog的一个置信区间出来
我们上面讲了计算λ值有不同的方法,那到底哪种方法计算出来的λ值更加可靠一些呢?我们可以通过另外一个函数boxcox_normplot来查看到底哪种方法计算出来的λ值更可靠。
boxcox_normplot(x, la, lb, plot=None, N=80)参数:
x:非正态数据
la,lb:λ值的上下界
plot:绘图的画布
N:横轴的坐标点个数
返回值:
lmbdas:通过box-cox算出来的多个λ值
ppcc:相关系数,可以理解成λ值的可靠程度
以上就是box-cox变换过程中用到的三个不同的函数,接下来我们给大家实际演示一下这三个函数如何使用。
首先,我们导入一份非正态数据,并绘制这份数据的概率密度图,需要这份数据的在公众号后台回复非正态数据,即可获得。
import pandas as pdimport numpy as np
import seaborn as sns
df = pd.read_excel(r"非正态数据集.xlsx")
sns.distplot(df["price"],color = "#D86457")
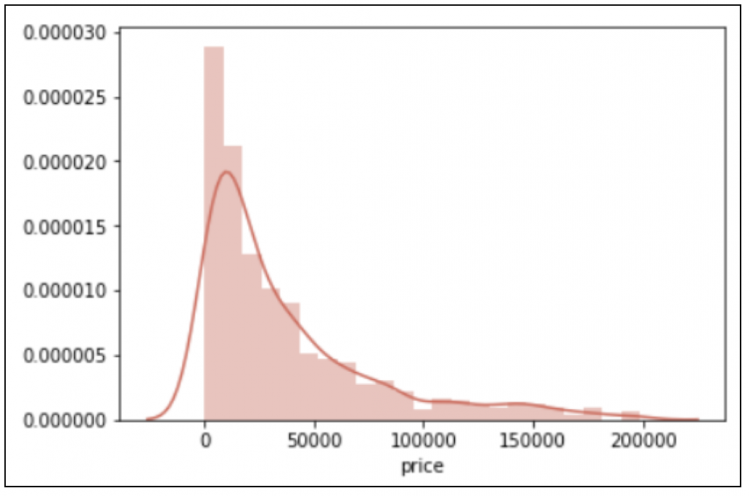
通过上面的概率密度图,我们可以看出这是一份偏态数据,也就是非正态。接下来我们先利用boxcox_normmax函数来寻找最优λ值,代码如下:
from scipy import statsstats.boxcox_normmax(df["price"])
---
返回:0.17896037184755484
在获得最优λ值以后,我们再利用boxcox函数来进行数据转换,具体代码如下:
x = stats.boxcox(df["price"],stats.boxcox_normmax(df["price"]))sns.distplot(x,color = "#D86457")
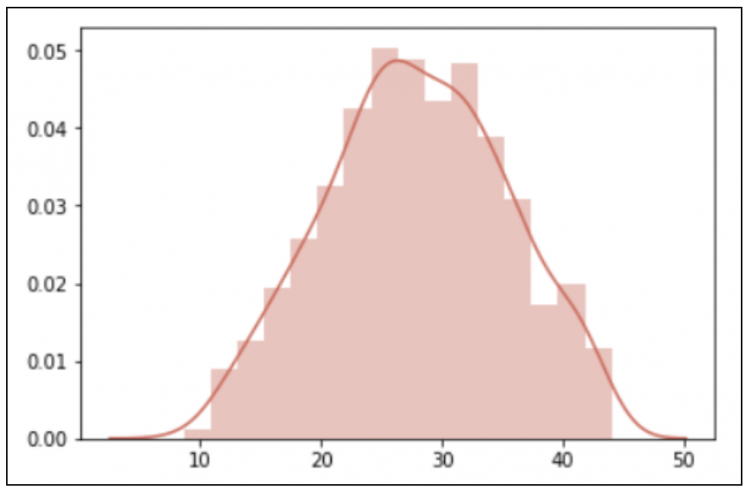
对转换后的数据再次进行概率密度图的绘制,我们可以看到,数据就很正态了。
接下来再来我们再看一下我们计算出来的λ值是不是最优的,具体代码如下:
fig = plt.figure()ax = fig.add_subplot(111)
stats.boxcox_normplot(df["price"], -20, 20,plot = ax)
plt.axvline(x = stats.boxcox_normmax(df["price"]),color = "#D86457")
plt.show()
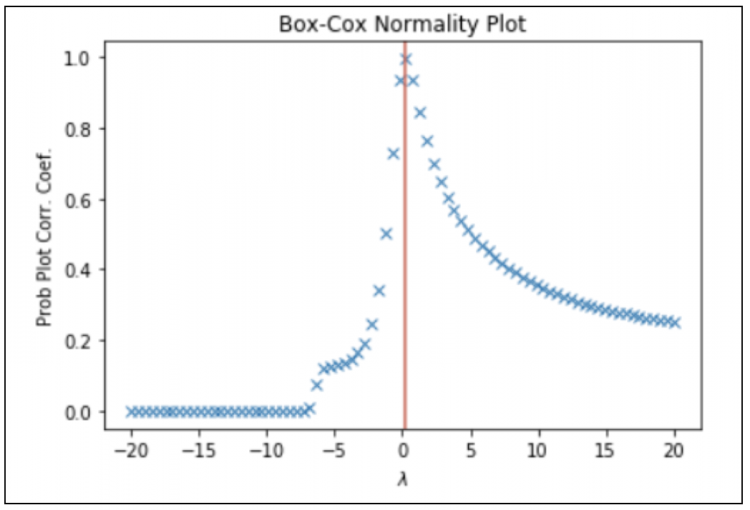
中间红色那条线的位置就是我们求出来最优的λ值,结果很吻合。
以上就是关于Box-Cox变换的理论和实战内容,大家多多练习。
mysql算法python数据库网页爬虫
阅读 30发布于 今天 06:44
本作品系原创,采用《署名-非商业性使用-禁止演绎 4.0 国际》许可协议
张俊红
公众号:《俊红的数据分析之路》,分享数据分析相关的内容。
1 声望
0 粉丝
张俊红
公众号:《俊红的数据分析之路》,分享数据分析相关的内容。
1 声望
0 粉丝
宣传栏
我们在前面讲过数据的正态性检验,介绍了检验数据是否正态的两种方法。这一节我们来看一下,如果数据不满足正态时该怎么办,答案就是将非正态数据通过Box-Cox变换进一步转换成符合正态分布的数据。这一篇就给大家分享下Box-Cox变换的具体内容。
Box-Cox变换是多种变换的总称,具体的公式如下: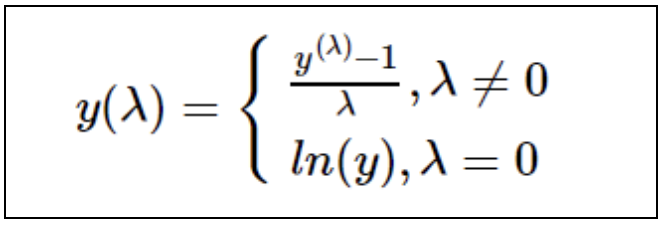
上面公式中y(λ)表示变换后的值,根据λ的值不同,属于不同的变换,当λ值取以下特定的几个值时就变成了特殊的数据变换:
- 当λ=0时,Box-Cox变换就变成了对数变换,y(λ) = ln(y);
- 当λ=0.5时,Box-Cox变换就变成了平方根变换,y(λ) = y^1/2
- 当λ=1时,Box-Cox变换变换就是它本身,y(λ) = y
- 当λ=2时,Box-Cox变换就变成了平方变化,y(λ) = y^2
- 当λ=-1时,Box-Cox变换就变成了倒数变化,y(λ) = 1/y。
λ值除了可以选择上述特定的值以外,还可以选择其他值,那当我们拿到一份非正态数据时,我们应该取λ值等于多少对齐进行变换呢?这个又该怎么定呢?
λ值取多少,我们可以利用Python中现成的函数,让函数自动去探索,然后返回给我们最优的值是多少就可以。这个函数就是boxcox_normmax,这个函数用来计算给定的非正态数据对应的最优λ值。
boxcox_normmax(x[, brack, method])参数:
x:非正态数据
brack: λ值搜索间隔,默认即可
method:计算λ值的方法,有pearsonr、mle、all三种可选,默认为pearsonr,即按照相关性的方法去计算,如果选all,则会返回各种方法的计算结果
返回值:
返回λ值
当我们得到最优的λ值以后,就可以根据λ值进行数据转换了,这个时候可以用另外的一个函数boxcox,这个函数是根据指定的λ值对原始数据进行转换。
boxcox(x[, lmbda, alpha])参数:
x:非正态数据
lambda:转换的λ值
alpha:计算置信区间时所用到的alpha值
返回值:
boxcox:经过转换以后的数据
maxlog:如果在传入时lambda参数值没有指定的话,该函数也会计算一个λ值出来
(min_ci, max_ci):如果lambda参数为空且alpha参数不为空时,会计算maxlog的一个置信区间出来
我们上面讲了计算λ值有不同的方法,那到底哪种方法计算出来的λ值更加可靠一些呢?我们可以通过另外一个函数boxcox_normplot来查看到底哪种方法计算出来的λ值更可靠。
boxcox_normplot(x, la, lb, plot=None, N=80)参数:
x:非正态数据
la,lb:λ值的上下界
plot:绘图的画布
N:横轴的坐标点个数
返回值:
lmbdas:通过box-cox算出来的多个λ值
ppcc:相关系数,可以理解成λ值的可靠程度
以上就是box-cox变换过程中用到的三个不同的函数,接下来我们给大家实际演示一下这三个函数如何使用。
首先,我们导入一份非正态数据,并绘制这份数据的概率密度图,需要这份数据的在公众号后台回复非正态数据,即可获得。
import pandas as pdimport numpy as np
import seaborn as sns
df = pd.read_excel(r"非正态数据集.xlsx")
sns.distplot(df["price"],color = "#D86457")

通过上面的概率密度图,我们可以看出这是一份偏态数据,也就是非正态。接下来我们先利用boxcox_normmax函数来寻找最优λ值,代码如下:
from scipy import statsstats.boxcox_normmax(df["price"])
---
返回:0.17896037184755484
在获得最优λ值以后,我们再利用boxcox函数来进行数据转换,具体代码如下:
x = stats.boxcox(df["price"],stats.boxcox_normmax(df["price"]))sns.distplot(x,color = "#D86457")

对转换后的数据再次进行概率密度图的绘制,我们可以看到,数据就很正态了。
接下来再来我们再看一下我们计算出来的λ值是不是最优的,具体代码如下:
fig = plt.figure()ax = fig.add_subplot(111)
stats.boxcox_normplot(df["price"], -20, 20,plot = ax)
plt.axvline(x = stats.boxcox_normmax(df["price"]),color = "#D86457")
plt.show()

中间红色那条线的位置就是我们求出来最优的λ值,结果很吻合。
以上就是关于Box-Cox变换的理论和实战内容,大家多多练习。
以上是 【Python】统计科学之分析遇到非正态数据该怎么办? 的全部内容, 来源链接: utcz.com/a/108955.html






得票时间