如何求出2个矩形四边最短距离?

• Z时代
• 2024-02-17
• 分类：IT

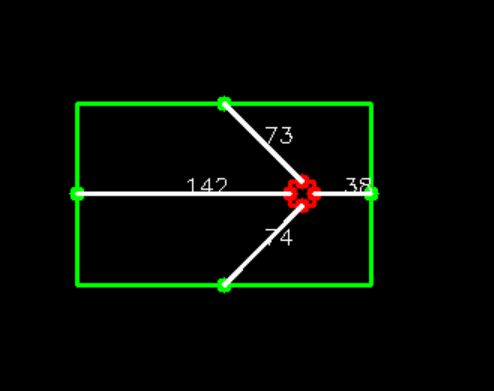
import cv2
import numpy as np
def draw_distance_lines(image, small_rect, big_rect):
    x1, y1, x2, y2 = small_rect
    bx1, by1, bx2, by2 = big_rect
    # 小矩形
    cv2.rectangle(image, (x1, y1), (x2, y2), (0, 0, 255), 2)
    small_centers = [(x1, (y1 + y2) // 2), (x2, (y1 + y2) // 2),
                     ((x1 + x2) // 2, y1), ((x1 + x2) // 2, y2)]
    for center in small_centers:
        cv2.circle(image, center, 5, (0, 0, 255), -1)
    # 大矩形
    cv2.rectangle(image, (bx1, by1), (bx2, by2), (0, 255, 0), 2)
    big_centers = [(bx1, (by1 + by2) // 2), (bx2, (by1 + by2) // 2),
                   ((bx1 + bx2) // 2, by1), ((bx1 + bx2) // 2, by2)]
    for center in big_centers:
        cv2.circle(image, center, 5, (0, 255, 0), -1)
    # 连接中心点并计算线条长度
    for small_center, big_center in zip(small_centers, big_centers):
        line_length = int(np.sqrt((big_center[0] - small_center[0])**2 + (big_center[1] - small_center[1])**2))
        cv2.line(image, small_center, big_center, (255, 255, 255), 2)
        cv2.putText(image, f"{line_length}", ((small_center[0] + big_center[0]) // 2, (small_center[1] + big_center[1]) // 2),
                    cv2.FONT_HERSHEY_SIMPLEX, 0.5, (255, 255, 255), 1)
# 定义矩形坐标列表
small_rectangles = [[201, 266, 217, 282]]
big_rectangles = [[59, 214, 255, 335]]
# 创建一个空白图像
image = np.zeros((500, 500, 3), dtype=np.uint8)
for i in range(len(small_rectangles)):
    small_rect = small_rectangles[i]
    big_rect = big_rectangles[i]
    draw_distance_lines(image, small_rect, big_rect)
# 显示图像
cv2.imshow("Rectangles with Distances", image)
cv2.waitKey(0)
cv2.destroyAllWindows()

如何改为 连接最短的距离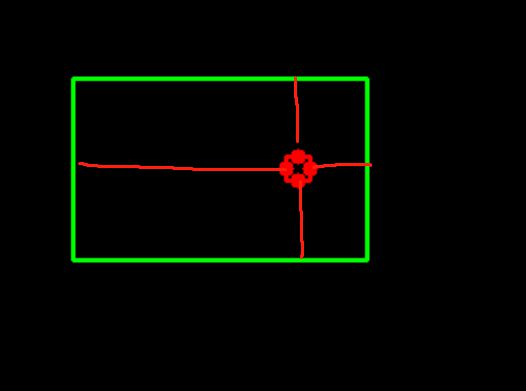

回答：

import matplotlib.pyplot as plt
import numpy as np
def draw_distance_lines(ax, small_rect, big_rect):
    x1, y1, x2, y2 = small_rect
    bx1, by1, bx2, by2 = big_rect
    # 小矩形
    ax.add_patch(plt.Rectangle((x1, y1), x2 - x1, y2 - y1, linewidth=2, edgecolor='r', facecolor='none'))
    small_centers = [(x1, (y1 + y2) // 2), (x2, (y1 + y2) // 2),
                     ((x1 + x2) // 2, y1), ((x1 + x2) // 2, y2)]
    for center in small_centers:
        ax.add_patch(plt.Circle(center, 5, color='r'))
    # 大矩形
    ax.add_patch(plt.Rectangle((bx1, by1), bx2 - bx1, by2 - by1, linewidth=2, edgecolor='g', facecolor='none'))
    big_centers = [(bx1, (by1 + by2) // 2), (bx2, (by1 + by2) // 2),
                   ((bx1 + bx2) // 2, by1), ((bx1 + bx2) // 2, by2)]
    for center in big_centers:
        ax.add_patch(plt.Circle(center, 5, color='g'))
    # 找到最短距离的中心点
    min_distance = float("inf")
    closest_small_center = None
    closest_big_center = None
    for small_center in small_centers:
        for big_center in big_centers:
            line_length = np.sqrt((big_center[0] - small_center[0])**2 + (big_center[1] - small_center[1])**2)
            if line_length < min_distance:
                min_distance = line_length
                closest_small_center = small_center
                closest_big_center = big_center
    # 绘制最短距离的线
    ax.plot([closest_small_center[0], closest_big_center[0]], [closest_small_center[1], closest_big_center[1]], 'w--')
    ax.text((closest_small_center[0] + closest_big_center[0]) // 2,
            (closest_small_center[1] + closest_big_center[1]) // 2,
            f"{int(min_distance)}", color='w', fontsize=12, ha='center')
# 定义矩形坐标列表
small_rectangles = [[201, 266, 217, 282]]
big_rectangles = [[59, 214, 255, 335]]
# 创建一个空白图像
fig, ax = plt.subplots()
ax.set_xlim(0, 500)
ax.set_ylim(0, 500)
ax.set_facecolor((0, 0, 0))
for i in range(len(small_rectangles)):
    small_rect = small_rectangles[i]
    big_rect = big_rectangles[i]
    draw_distance_lines(ax, small_rect, big_rect)
plt.show()

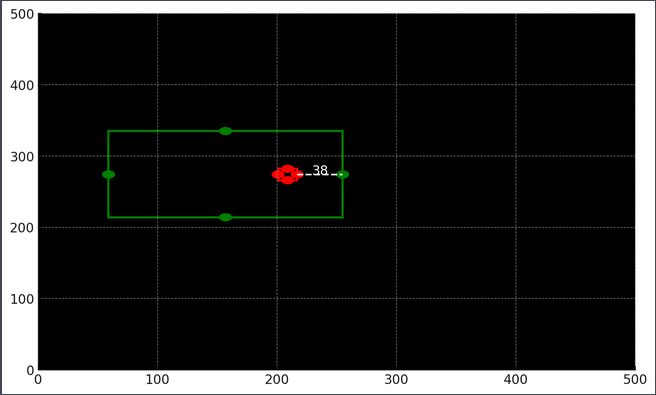
回答：

无非就是改一下big_centers里面的四个点坐标。

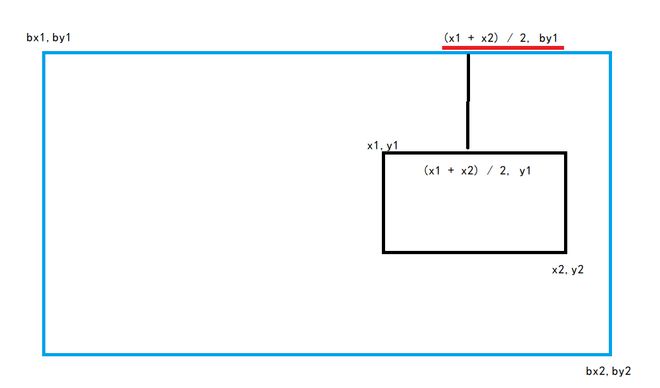
看了你的算法，无论是大矩形还是小矩形求取线段中点坐标都是按照平行于x轴或y轴来计算的，运用初中学习的坐标系知识，那大矩形边上平行于小矩形线段中点的四个点不就好算了吗

以上是 如何求出2个矩形四边最短距离? 的全部内容， 来源链接： utcz.com/p/938999.html