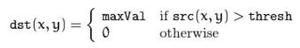opencv求解区域的内接矩形
实验室项目中,希望求取一个近似圆形区域的质心,原本使用最小外接圆的质心来等效为该区域质心。但是由于部分区域的形状过于不规则导致发生质心偏移现象。如下图:
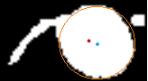
蓝色为实际要求质心。红色为等效圆质心
为获取较为准确的质心,拟用最大内接矩形的中心作为该区域质心。
采用改进的中心扩散法求内接矩形:先以最小外接矩的中心作为算法的起点进行中心扩散。得到一个内解矩形,在对最小外接矩的中心进行8邻域的遍历,应用中心扩散法分别求取内接矩,以面积最大的内接矩作为最大内接矩。
使用Opencv关键代码如下:
/**
* @brief 求取连通区域内接矩
* @param img:输入图像,单通道二值图,深度为8
* @param center:最小外接矩的中心
* @return 最大内接矩形
* 基于中心扩展算法
*/
cv::Rect InSquare(Mat &img,const Point center)
{
// --[1]参数检测
if(img.empty()||
img.channels()>1
||img.depth()>8)
return Rect();
//[1]
// --[2] 初始化变量
int edge[4];
edge[0]=center.y+1;//top
edge[1]=center.x+1;//right
edge[2]=center.y-1;//bottom
edge[3]=center.x-1;//left
//[2]
// --[3]边界扩展(中心扩散法)
bool EXPAND[4]={1,1,1,1};//扩展标记位
int n=0;
while (EXPAND[0]||EXPAND[1]||EXPAND[2]||EXPAND[3])
{
int edgeID=n%4;
EXPAND[edgeID]=expandEdge(img,edge,edgeID);
n++;
}
//[3]
qDebug()<<edge[0]<<edge[1]<<edge[2]<<edge[3];
Point tl=Point(edge[3],edge[0]);
Point br=Point(edge[1],edge[2]);
return Rect(tl,br);
}
/**
* @brief expandEdge 扩展边界函数
* @param img:输入图像,单通道二值图,深度为8
* @param edge 边界数组,存放4条边界值
* @param edgeID 当前边界号
* @return 布尔值 确定当前边界是否可以扩展
*/
bool expandEdge(const Mat & img, int edge[], const int edgeID)
{
//[1] --初始化参数
int nc=img.cols;
int nr=img.rows;
switch (edgeID) {
case 0:
if(edge[0]>nr)
return false;
for(int i=edge[3];i<=edge[1];++i)
{
if(img.at<uchar>(edge[0],i)==0)
return false;
}
edge[0]++;
return true;
break;
case 1:
if(edge[1]>nc)
return false;
for(int i=edge[2];i<=edge[0];++i)
{
if(img.at<uchar>(i,edge[1])==0)
return false;
}
edge[1]++;
return true;
break;
case 2:
if(edge[2]<0)
return false;
for(int i=edge[3];i<=edge[1];++i)
{
if(img.at<uchar>(edge[2],i)==0)
return false;
}
edge[2]--;
return true;
break;
case 3:
if(edge[3]<0)
return false;
for(int i=edge[2];i<=edge[0];++i)
{
if(img.at<uchar>(i,edge[3])==0)
return false;
}
edge[3]--;
return true;
break;
default:
return false;
break;
}
}
效果:
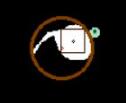
黑色为内接矩中心,红色为最小外接圆中心
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持。
以上是 opencv求解区域的内接矩形 的全部内容, 来源链接: utcz.com/p/245360.html