如何只使用BP反向传播的神经网络完成MNIST手写数字识别?

这真的是一个非常非常基础的问题,但还是想厚着脸问一下。
首先,我是从这篇介绍神经网络的入门文章了解到神经网络的工作原理。
然后在文章里的例子是,输入两个整数型的值,一个体重,一个身高,然后预测的是性别。在训练的时候,是通过反向传播,反向传播的代码如下
def train(self, data, all_y_trues): '''
- data is a (n x 2) numpy array, n = # of samples in the dataset.
- all_y_trues is a numpy array with n elements.
Elements in all_y_trues correspond to those in data.
'''
learn_rate = 0.1
epochs = 1000 # number of times to loop through the entire dataset
for epoch in range(epochs):
for x, y_true in zip(data, all_y_trues):
# --- Do a feedforward (we'll need these values later)
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# --- Calculate partial derivatives.
# --- Naming: d_L_d_w1 represents "partial L / partial w1"
d_L_d_ypred = -2 * (y_true - y_pred)
# Neuron o1
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# Neuron h1
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# Neuron h2
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# --- Update weights and biases
# Neuron h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# Neuron h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# Neuron o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# --- Calculate total loss at the end of each epoch
if epoch % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = mse_loss(all_y_trues, y_preds)
print("Epoch %d loss: %.3f" % (epoch, loss))
我的问题是,在MNIST训练手写分类,因为输入的是一个28*28的数组,可是按照上面的思路,输入值为整数型,那么该怎么处理呢?
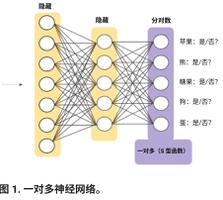
然后,MNIST训练要用到很多的神经元,训练隐藏层里面的神经元很多,那么按照上面的做法,那我得写多少个w,多少个b啊?光是隐藏层里两个神经元就难得写了,多了那岂不是更麻烦?该如何解决呢?
希望不吝解答,Thanks♪(・ω・)ノ
回答:
手把手教你搭建BP神经网络,并实现手写mnist手写数字识别
原来是用向量,原理还没细看,应该是这个了
回答:
比如从$l-1$层到$l$层的权重矩阵为$w^l$,形状为$[m,n]$。
前向传播的过程为
$$a^{l-1}*w^l=z^{l}$$
反向传播的过程为
$$\frac{\partial C}{\partial w^l}=\frac{\partial C}{\partial z^l} a^{l-1}$$
$a$表示激活值,$z$表示激活之前的值,$C$表示损失函数。
前向传播和反向传播都是矩阵运算的,而不是单个权重。你应该定义一个类,来保存每一层的权重矩阵及其对应的梯度,类中,你需要手动实现前向传播函数和反向传播函数。不知道是否能帮助你
以上是 如何只使用BP反向传播的神经网络完成MNIST手写数字识别? 的全部内容, 来源链接: utcz.com/a/164071.html