二分搜索树BST前序中序后序(递归和非递归实现)和层序遍历

Z时代
2024-01-10
分类：综合

二分搜索树前序中序后序遍历理解

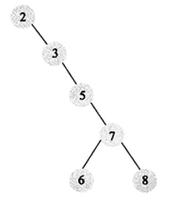
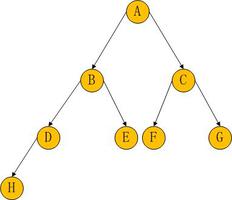
根据获取中间节点的不同,来分为前序中序后序,如图⇓

先序遍历 -> 先打印中间节点,再依次打印左节点和右节点

中序遍历 -> 先打印左节点,再打印中间节点,最后打印右节点

后序遍历 -> 先依次打印左节点和右节点,再打印中间节点

二分搜索树前序中序后序遍历节点访问顺序图解

上图是一棵示例的二分搜索树,满足左节点<中间节点<右节点

跟随图中的箭头,依次访问

22->13->12->12->12->13->18->18->18->13->22->25->23->23->23->25->26->26->29->29->26->25->22

每个节点都被访问三次

先序遍历 -> 按第一次访问顺序打印,如图,由根节点22出发.依次打印

22->13->12->18->25->23->26->29

中序遍历 -> 按第二次访问顺序打印,如图,由根节点出发(此时是第一次访问根节点,不打印),依次打印

12->13->18->22->23->25->26->29

后序遍历 -> 按第三次访问顺序打印.如图,由根节点出发(此时是第一次访问根节点,不打印),依次打印

12->18->13->23->29->26->25->22

实现

创建一个类,命名为BinarySearchTree

由于在添加查找操作中都需要对节点进行比较,所以需要实现继承比较类Comparable

并且实例代码支持泛型

public class BinarySearchTree<E extends Comparable<E>> {
    private class Node {
        public E e;
        public Node left, right;
        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }
    private Node root;
}

递归实现

前序遍历/深度优先遍历

    // 二分搜索树的前序遍历(暴露给用户调用)
    public void preOrder() {
        preOrder(root);
    }
    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node) {
        if (node == null)
            return;
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

中序遍历

    // 二分搜索树的中序遍历(暴露给用户调用)
    public void inOrder() {
        inOrder(root);
    }
    // 中序遍历以node为根的二分搜索树, 递归算法
    private void inOrder(Node node) {
        if (node == null)
            return;
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

后序遍历

    // 二分搜索树的后序遍历(暴露给用户调用)
    public void postOrder() {
        postOrder(root);
    }
    // 后序遍历以node为根的二分搜索树, 递归算法
    private void postOrder(Node node) {
        if (node == null)
            return;
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

非递归实现

本次实现并没有使用教科书上的实现方式,改为模拟系统栈的形式实现

在类中加入内部类

    private class Command{
        String s;   // go, print
        Node node;
        Command(String s, Node node){
            this.s = s;
            this.node = node;
        }
    };

前序遍历/深度优先遍历

 // 二分搜索树的非递归前序遍历,其中print表示输出,go表示递归
    public void preOrderNR() {
        if (root == null) {
            return;
        }
        Stack<Command> stack = new Stack<>();
        stack.push(new Command("go", root));
        while (!stack.empty()) {
            Command command = stack.pop();
            if ("print".equals(command.s)) {
                System.out.println(command.node.e);
            } else {
                if (command.node.right != null) {
                    stack.push(new Command("go", command.node.right));
                }
                if (command.node.left != null) {
                    stack.push(new Command("go", command.node.left));
                }
                stack.push(new Command("print", command.node));
            }
        }
    }

中序遍历

    // 二分搜索树的非递归中序遍历,其中print表示输出,go表示递归
    public void inOrderNR() {
        if (root == null) {
            return;
        }
        Stack<Command> stack = new Stack<Command>();
        stack.push(new Command("go", root));
        while (!stack.empty()) {
            Command command = stack.pop();
            if ("print".equals(command.s)) {
                System.out.println(command.node.e);
            } else {
                if (command.node.right != null)
                    stack.push(new Command("go", command.node.right));
                stack.push(new Command("print", command.node));
                if (command.node.left != null)
                    stack.push(new Command("go", command.node.left));
            }
        }
    }

后序遍历

// 二分搜索树的非递归后序遍历,其中print表示输出,go表示递归
    public void postOrderNR() {
        if (root == null) {
            return;
        }
        Stack<Command> stack = new Stack<Command>();
        stack.push(new Command("go", root));
        while (!stack.empty()) {
            Command command = stack.pop();
            if ("print".equals(command.s)) {
                System.out.println(command.node.e);
            } else {
                assert "go".equals(command.s);
                stack.push(new Command("print", command.node));
                if (command.node.right != null) {
                    stack.push(new Command("go", command.node.right));
                }
                if (command.node.left != null) {
                    stack.push(new Command("go", command.node.left));
                }
            }
        }
    }

二分搜索树的层序遍历,即广度优先遍历

层序遍历,顾名思义就是按树的深度,从根节点开始,一层一层向底部遍历,如图⇓,输出结果是

22->13->25->12->18->23->26->29

    // 二分搜索树的层序遍历
    public void levelOrder() {
        if (root == null) {
            return;
        }
        Queue<Node> q = new LinkedList<>();
        q.add(root);
        while (!q.isEmpty()) {
            Node cur = q.remove();
            System.out.println(cur.e);
            if (cur.left != null) {
                q.add(cur.left);
            }
            if (cur.right != null) {
                q.add(cur.right);
            }
        }
    }