二叉树递归迭代及morris层序前中后序遍历详解

分析二叉树的前序,中序,后序的遍历步骤
1.层序遍历
方法一:广度优先搜索
(以下解释来自leetcode官方题解)
我们可以用广度优先搜索解决这个问题。
我们可以想到最朴素的方法是用一个二元组 (node, level) 来表示状态,它表示某个节点和它所在的层数,每个新进队列的节点的 level 值都是父亲节点的 level 值加一。最后根据每个点的 level 对点进行分类,分类的时候我们可以利用哈希表,维护一个以 level 为键,对应节点值组成的数组为值,广度优先搜索结束以后按键 level 从小到大取出所有值,组成答案返回即可。
考虑如何优化空间开销:如何不用哈希映射,并且只用一个变量 node 表示状态,实现这个功能呢?
我们可以用一种巧妙的方法修改广度优先搜索:
- 首先根元素入队
- 当队列不为空的时候,
求当前队列的长度 S_i;
依次从队列中取 S_i 个元素进行拓展,然后进入下一次迭代.
它和普通广度优先搜索的区别在于,普通广度优先搜索每次只取一个元素拓展,而这里每次取 S_i个元素。在上述过程中的第 i 次迭代就得到了二叉树的第 i 层的 S_i 个元素。
为什么这么做是对的呢?我们观察这个算法,可以归纳出这样的循环不变式:第 i 次迭代前,队列中的所有元素就是第 i 层的所有元素,并且按照从左向右的顺序排列。证明它的三条性质(你也可以把它理解成数学归纳法):
初始化:i=1 的时候,队列里面只有 root,是唯一的层数为 1 的元素,因为只有一个元素,所以也显然满足「从左向右排列」;
保持:如果 i=k 时性质成立,即第 k 轮中出队 S_k的元素是第 k 层的所有元素,并且顺序从左到右。因为对树进行广度优先搜索的时候由低 k 层的点拓展出的点一定也只能是 k+1 层的点,并且 k+1 层的点只能由第 k 层的点拓展到,所以由这 S_k 个点能拓展到下一层所有的 S_k+1 个点。又因为队列的先进先出(FIFO)特性,既然第 k 层的点的出队顺序是从左向右,那么第 k+1 层也一定是从左向右。至此,我们已经可以通过数学归纳法证明循环不变式的正确性。
终止:因为该循环不变式是正确的,所以按照这个方法迭代之后每次迭代得到的也就是当前层的层次遍历结果。至此,我们证明了算法是正确的。
广度优先搜索的简化步骤为
初始化队列 q,并将根节点 root 加入到队列中;
当队列不为空时:
队列中弹出节点 node,加入到结果中;
如果左子树非空,左子树加入队列;
如果右子树非空,右子树加入队列;
由于题目要求每一层保存在一个子数组中,所以我们额外加入了 level 保存每层的遍历结果,并使用 for 循环来实现。
看个图例用以说明:
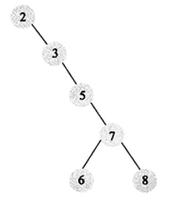
广度优先需要用队列作为辅助结构,我们先将根节点放到队列中,然后不断遍历队列。

首先拿出根节点,如果左子树/右子树不为空,就将他们放入队列中。第一遍处理完后,根节点已经从队列中拿走了,而根节点的两个孩子已放入队列中了,现在队列中就有两个节点 2 和 5。

第二次处理,会将 2 和 5 这两个节点从队列中拿走,然后再将 2 和 5 的子节点放入队列中,现在队列中就有三个节点 3,4,6。

我们把每层遍历到的节点都放入到一个结果集中,最后返回这个结果集就可以了。
public List<List<Integer>> levelOrder(TreeNode root) {
//返回的结果
List<List<Integer>> res = new ArrayList<List<Integer>>();
if(null == root){
return res;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
//根节点入队
queue.add(root);
while(!queue.isEmpty()){
//一层的结果
List<Integer> level = new ArrayList<Integer>();
int levelCount = queue.size();
//添加节点到一层的List中去
for(int i = 0; i < levelCount ; i ++){
//节点出队
TreeNode node = queue.remove();
//节点的左子树入队
if(node.left != null){
queue.add(node.left);
}
//节点的右子树入队
if(node.right != null){
queue.add(node.right);
}
level.add(node.val);
}
res.add(level);
}
return res;
}
方法二:递归
用广度优先处理是很直观的,可以想象成是一把刀横着切割了每一层,但是深度优先遍历就不那么直观了。

我们开下脑洞,把这个二叉树的样子调整一下,摆成一个田字形的样子。田字形的每一层就对应一个 list。

按照深度优先的处理顺序,会先访问节点 1,再访问节点 2,接着是节点 3。
之后是第二列的 4 和 5,最后是第三列的 6。
每次递归的时候都需要带一个 index(表示当前的层数),也就对应那个田字格子中的第几行,如果当前行对应的 list 不存在,就加入一个空 list 进去。

public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
if(root==null) {
return res;
}
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
//将根节点放入队列中,然后不断遍历队列
queue.add(root);
while(queue.size()>0) {
//获取当前队列的长度,这个长度相当于 当前这一层的节点个数
int size = queue.size();
ArrayList<Integer> tmp = new ArrayList<Integer>();
//将队列中的元素都拿出来(也就是获取这一层的节点),放到临时list中
//如果节点的左/右子树不为空,也放入队列中
for(int i=0;i<size;++i) {
TreeNode t = queue.remove();
tmp.add(t.val);
if(t.left!=null) {
queue.add(t.left);
}
if(t.right!=null) {
queue.add(t.right);
}
}
//将临时list加入最终返回结果中
res.add(tmp);
}
return res;
}
2.前序遍历
2.1先输出当前节点(初始的时候是root节点)
2.2如果左子节点不为空,则递归继续前序遍历
2.3如果右子节点不为空,则递归继续前序遍历
3.中序遍历
3.1如果当前节点的左子节点不为空,则递归中序遍历
3.2输出当前节点
3.3如果当前节点的右子节点不为空,则递归中序遍历
4.后序遍历
4.1如果当前节点的左子节点不为空,则递归后序遍历
4.2如果当前节点的右子节点不为空,则递归后序遍历
4.3输出当前节点

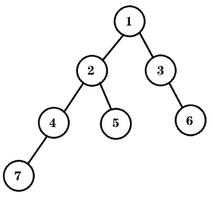
如果你按照 根节点 -> 左孩子 -> 右孩子 的方式遍历,即「先序遍历」,每次先遍历根节点,遍历结果为 1 2 4 5 3 6 7;
同理,如果你按照 左孩子 -> 根节点 -> 右孩子 的方式遍历,即「中序序遍历」,遍历结果为 4 2 5 1 6 3 7;
如果你按照 左孩子 -> 右孩子 -> 根节点 的方式遍历,即「后序序遍历」,遍历结果为 4 5 2 6 7 3 1;
最后,层序遍历就是按照每一层从左向右的方式进行遍历,遍历结果为 1 2 3 4 5 6 7。
递归解法
由于层次遍历的递归解法不是主流,因此只介绍前三种的递归解法
前序遍历--递归
public List<Integer> preorderTraversal(TreeNode root) {
//递归
List<Integer> list = new ArrayList<>();
preOrder(root,list);
return list;
}
public void preOrder(TreeNode root,List<Integer> list){
if(root == null){
return;
}
list.add(root.val);
preOrder(root.left,list);
preOrder(root.right,list);
}
中序遍历--递归
public List<Integer> inorderTraversal(TreeNode root) {
//递归
List<Integer> list = new LinkedList<>();
inOrder(root,list);
return list;
}
public void inOrder(TreeNode root,List<Integer> list){
if(root == null){
return;
}
inOrder(root.left,list);
list.add(root.val);
inOrder(root.right,list);
}
后序遍历--递归
public List<Integer> postorderTraversal(TreeNode root) {
//递归
List<Integer> list = new LinkedList<>();
postOrder(root,list);
return list;
}
public void postOrder(TreeNode root,List<Integer> list){
if(root == null){
return;
}
postOrder(root.left,list);
postOrder(root.right,list);
list.add(root.val);
}
三种递归遍历的总结:递归终止的条件为碰到空节点。
迭代解法
前序遍历--迭代
核心思想:
1.每拿到一个节点就把它保存在栈中
2.继续对这个节点的左子树重复过程1,直到左子树为空
3.因为保存在栈中的节点都遍历了左子树但是没有遍历右子树,所以对栈中节点出栈并对它的右子树重复过程1
4.直到遍历完所有节点
public List<Integer> preorderTraversal(TreeNode root) {
//迭代
List<Integer> list = new ArrayList<>();
if(root == null){
return list;
}
Deque<TreeNode> stack = new LinkedList<TreeNode>();
//临时节点,帮助遍历二叉树
TreeNode node = root;
//栈的作用是用来短暂的保存遍历节点的值,以助于最后值的返回
while(!stack.isEmpty() || node != null){
while(node != null){
list.add(node.val);
stack.push(node);
node = node.left;
}
node = stack.pop();
node = node.right;
}
return list;
}
中序遍历--迭代
public List<Integer> inorderTraversal(TreeNode root) {
//迭代
List<Integer> list = new ArrayList<>();
if(root == null){
return list;
}
Deque<TreeNode> stack = new LinkedList<>();
while(!stack.isEmpty() || root != null){
while(root != null){
stack.push(root);
root = root.left;
}
root = stack.pop();
list.add(root.val);//出栈的时候才将父节点 的值加入到结果中
root = root.right;
}
return list;
}
和前序遍历的代码完全相同,只是在出栈的时候才将父节点 的值加入到结果中。
后序遍历--迭代
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<Integer> list = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.isEmpty()) {
if (root != null) {
stack.push(root);
list.addFirst(root.val);//addFirst():向链表首部添加元素
root = root.right;
} else {
root = stack.pop();
root = root.left;
}
}
return list;
}
三种迭代解法的总结:
前序遍历和后序遍历之间的关系:
前序遍历顺序为:根 -> 左 -> 右
后序遍历顺序为:左 -> 右 -> 根
如果1: 将前序遍历中节点插入结果链表尾部的逻辑,修改为将节点插入结果链表的头部
那么结果链表就变为了:右 -> 左 -> 根
如果2: 将遍历的顺序由从左到右修改为从右到左,配合如果1
那么结果链表就变为了:左 -> 右 -> 根
这刚好是后序遍历的顺序
基于这两个思路,想一下如何处理:
修改前序遍历代码中,节点写入结果链表的代码,将插入队尾修改为插入队首
修改前序遍历代码中,每次先查看左节点再查看右节点的逻辑,变为先查看右节点再查看左节点
前序遍历和中序遍历之间的关系:
和前序遍历的代码完全相同,只是在出栈的时候才将父节点的值加入到结果中。
Morris遍历
遍历特点:Morris 遍历利用了树中大量空闲指针的特性
当前节点cur,一开始cur来到整树头
1)cur无左树,cur = cur.right(cur右移)
2)cur有左树,找到左树最右节点,mostright;此时我们又可以分为两种情况,一种是叶子节点添加 right 指针的情况,一种是去除叶子节点 right 指针的情况
A.mostright 的右指针指向null的mostright.right = cur, cur = cur.left(cur左移)
B.mostright 的右指针指向cur的mostright.right = null(为了防止重复执行,则需要去掉 right 指针), cur = cur.right(cur右移)
当cur == null时,整个过程结束。
遍历特点:有左树节点必遍历到两次,没有左树的节点必遍历到一次
public static void morris(Node head){
if(head == null){
return;
}
Node cur = head;
Node mostRight = null;
while(cur != null){
//cur有没有左树
mostRight = cur.left;
if(mostRight != null){//有左树的情况
//找到cur左树上,真实的最右节点
//前者说明是第一次来到当前的cur,后者说明是第二次来到当前的cur
while(mostRight.right != null && mostRight.right != cur){
mostRight = mostRight.right;
}
//从while中出来,mostRight一定是cur左树上的最右节点
if(mostRight.right == null){
mostRight.right = cur;
cur = cur.left;
continue;//结束的是外层的循环!!!!!!!!!!!!!
}else{//走到这里意味着:mostRight.right == cur
mostRight.right = null;
}
}
//cur没有左树
cur = cur.right;
}
}






空间复杂度:利用空闲的指针,使用了两个变量完成了遍历,空间复杂度是常数级别的
时间复杂度:
morris--前序遍历
第一次来到一个节点,就打印;第二次来到这个节点,不打印
public static void morrisPre(Node head){
if(head == null){
return;
}
Node cur = head;
Node mostRight = null;
while(cur != null){
mostRight = cur.left;
if(mostRight != null){
while(mostRight.right != null && mostRight.right != cur){
mostRight = mostRight.right;
}
if(mostRight.right == null){
mostRight.right = cur;
System.out.print(cur.value + " ");
cur = cur.left;
continue;
}else{
mostRight.right = null;
}
}else{
System.out.print(cur.value + " ");
}
cur = cur.right;
}
System.out.println();
}
morris--中序遍历
对于能回到自己两次的节点,第二次时打印,对于只能来到自己一次的节点,直接打印
只要一个节点要往右移动,就打印
public static void morrisIn(Node head){
if(head == null){
return;
}
Node cur = head;
Node mostRight = null;
while(cur != null){
mostRight = cur.left;
if(mostRight != null){
while(mostRight.right != null && mostRight.right != cur){
mostRight = mostRight.right;
}
if(mostRight.right == null){
mostRight.right = cur;
cur = cur.left;
continue;
}else{
mostRight.right = null;
}
}
System.out.print(cur.value + " ");
cur = cur.right;
}
System.out.println();
}
morris--后序遍历:
public static void morrisPos(Node head) {
if(head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while(cur != null) {
mostRight = cur.left;
if(mostRight != null) {
while(mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if(mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
}else {
mostRight.right = null;
printEdge(cur.left);//逆序打印左树的右边界
}
}
cur = cur.right;
}
printEdge(head);//最后打印整棵树的右边界
System.out.println();
}
public static void printEdge(Node head) {
Node tail = reverseEdge(head);
Node cur = tail;
while(cur != null) {
System.out.print(cur.value + " ");
cur = cur.right;
}
reverseEdge(tail);
}
private static Node reverseEdge(Node from) {
Node pre = null;
Node next = null;
while(from != null) {
next = from.right;
from.right = pre;
pre = from;
from = next;
}
return pre;
}
Morris后序遍历比较复杂,可以看看相关的视频讲解--左神算法系列。
以上就是二叉树递归迭代及morris层序前中后序遍历详解的详细内容,更多关于二叉树递归迭代遍历详解的资料请关注其它相关文章!
以上是 二叉树递归迭代及morris层序前中后序遍历详解 的全部内容, 来源链接: utcz.com/p/250989.html