机器学习|支持向量机参数求解

coding

—

支持向量机的简称为SVM，能在已知样本点很少情况下，获得很好的分类效果。

—

SVM分类两个点

已知两个样本点，如果用SVM模型，决策边界就是线g，它的斜率为已知两个样本点斜率的垂直方向，并经过两个点的中点。

这条线g就是SVM认为的分类两个样本点的最好边界线。

—

SVM分类多个点

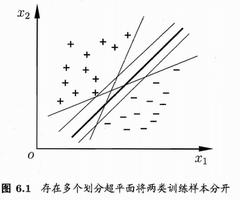
添加更多的样本点，但是有意识地让它们符合上面的分布，此时的最佳决策边界发生变化了吗？没有。

样本点虽然多了，但是SVM认为起到支持作用的还是那两个点，support vector就是它们，名字得来了，当然因此决策边界也未变。

以上这些都是直接观察出来的，计算机是如何做这个事的？

—

启发

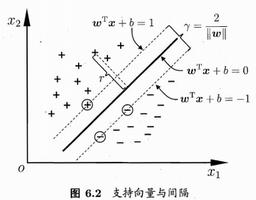
03节还启发我们，SVM建立决策边界时，只关心距离决策边界最近的那两个样本点，然后取距离它们都最远的决策边g ，认为g就是最佳决策边界。

—

趁热打铁：SVM目标函数

有了以上基础，SVM目标函数的结构差不多就知道了：max ( min() )，SVM添加了一个约束，得到的好处是目标函数更精简了：

arg max 1/||w||

s.t., y*f(x)>=1

注意，这个更精简的目标函数，必须满足上面的约束，它们是共生关系，缺一不可。

—

最大值转化为求最小值

机器学习中，遇到目标函数求最大值的，都会转化为求最小值，常规套路，SVM也不例外。

它也很简单，分母最小，原式便能最大，即：

arg min 0.5*||w||^2

s.t., y * f(x)>=1

目标函数为什么带有系数0.5，没有特殊原因，只不过求导时，0.5*2化简方便。

这是常见的二次规划问题，求解方法有很多种，拉格朗日方法、Lemke方法、内点法、有效集法、椭球算法等。

SVM的以上目标函数求解选用了拉格朗日方法，可以查阅资料，了解此求解方法，里面还用到KKT，转化为先求w,b的最小值，然后再求alfa_i的最大值问题，进而求得参数w和b，至此完毕。

SVM还考虑了软间隔，核函数问题，这部分接下来推送。

算法channel会有系统地，认真地推送：机器学习（包含深度学习，强化学习等）的理论，算法，实践，源码实现。期待您的参与！

本文分享自微信公众号 - Python与算法社区（alg-channel）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。