java 关于二叉搜索树,平衡二叉树,b树,二叉堆的几段代码

最近重新学习数据结构和算法,刚刚看完java版的这几个数据结构,比较浅显易懂,有兴趣的可以自己去调试学习,关于这几个的介绍网上很多。
二叉搜索树,比较简单的树结构了
package com.jwetherell.algorithms.data_structures;import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
import java.util.Queue;
/**
* A binary search tree (BST), which may sometimes also be called an ordered or
* sorted binary tree, is a node-based binary tree data structure which has the
* following properties: 1) The left subtree of a node contains only nodes with
* keys less than the node's key. 2) The right subtree of a node contains only
* nodes with keys greater than the node's key. 3) Both the left and right
* subtrees must also be binary search trees.
*
* http://en.wikipedia.org/wiki/Binary_search_tree
*
* @author Justin Wetherell <phishman3579@gmail.com>
*/
public class BinarySearchTree<T extends Comparable<T>> {
private int modifications = 0;
protected static final Random RANDOM = new Random();
protected enum Position { LEFT, RIGHT };
protected Node<T> root = null;
protected int size = 0;
protected INodeCreator<T> creator = null;
/**
* Default constructor.
*/
public BinarySearchTree() { }
/**
* Constructor with external Node creator.
*/
public BinarySearchTree(INodeCreator<T> creator) {
this.creator = creator;
}
/**
* Add value to the tree. Tree can contain multiple equal values.
*
* @param value T to add to the tree.
* @return True if successfully added to tree.
*/
public boolean add(T value) {
Node<T> nodeAdded = this.addValue(value);
return (nodeAdded!=null);
}
/**
* Add value to the tree and return the Node that was added. Tree can
* contain multiple equal values.
*
* @param value T to add to the tree.
* @return Node<T> which was added to the tree.
*/
protected Node<T> addValue(T value) {
Node<T> newNode = null;
if (this.creator == null) newNode = new Node<T>(null, value);
else newNode = this.creator.createNewNode(null, value);
//If root is null, assign
if (root == null) {
root = newNode;
size++;
return newNode;
}
Node<T> node = root;
while (node != null) {
if (newNode.id.compareTo(node.id) <= 0) {
//Less than or equal to goes left
if (node.lesser == null) {
// New left node
node.lesser = newNode;
newNode.parent = node;
size++;
return newNode;
} else {
node = node.lesser;
}
} else {
//Greater than goes right
if (node.greater == null) {
// New right node
node.greater = newNode;
newNode.parent = node;
size++;
return newNode;
} else {
node = node.greater;
}
}
}
return newNode;
}
/**
* Does the tree contain the value.
*
* @param value T to locate in the tree.
* @return True if tree contains value.
*/
public boolean contains(T value) {
Node<T> node = getNode(value);
return (node != null);
}
/**
* Locate T in the tree.
*
* @param value T to locate in the tree.
* @return Node<T> representing first reference of value in tree or NULL if not found.
*/
protected Node<T> getNode(T value) {
Node<T> node = root;
while (node != null && node.id!=null) {
if (value.compareTo(node.id) == 0) {
return node;
} else if (value.compareTo(node.id) < 0) {
node = node.lesser;
} else {
node = node.greater;
}
}
return null;
}
/**
* Rotate tree left at sub-tree rooted at node.
*
* @param node Root of tree to rotate left.
*/
protected void rotateLeft(Node<T> node) {
Position parentPosition = null;
Node<T> parent = node.parent;
if (parent!=null) {
if (node.equals(parent.lesser)) {
//Lesser
parentPosition = Position.LEFT;
} else {
//Greater
parentPosition = Position.RIGHT;
}
}
Node<T> greater = node.greater;
node.greater = null;
Node<T> lesser = greater.lesser;
greater.lesser = node;
node.parent = greater;
node.greater = lesser;
if (lesser!=null) lesser.parent = node;
if (parentPosition!=null) {
if (parentPosition==Position.LEFT) {
parent.lesser = greater;
} else {
parent.greater = greater;
}
greater.parent = parent;
} else {
root = greater;
greater.parent = null;
}
}
/**
* Rotate tree right at sub-tree rooted at node.
*
* @param node Root of tree to rotate left.
*/
protected void rotateRight(Node<T> node) {
Position parentPosition = null;
Node<T> parent = node.parent;
if (parent!=null) {
if (node.equals(parent.lesser)) {
//Lesser
parentPosition = Position.LEFT;
} else {
//Greater
parentPosition = Position.RIGHT;
}
}
Node<T> lesser = node.lesser;
node.lesser = null;
Node<T> greater = lesser.greater;
lesser.greater = node;
node.parent = lesser;
node.lesser = greater;
if (greater!=null) greater.parent = node;
if (parentPosition!=null) {
if (parentPosition==Position.LEFT) {
parent.lesser = lesser;
} else {
parent.greater = lesser;
}
lesser.parent = parent;
} else {
root = lesser;
lesser.parent = null;
}
}
/**
* Get greatest node in sub-tree rooted at startingNode. The
* search does not include startingNode in it's results.
*
* @param startingNode Root of tree to search.
* @return Node<T> which represents the greatest node in the
* startingNode sub-tree or NULL if startingNode has no greater
* children.
*/
protected Node<T> getGreatest(Node<T> startingNode) {
if (startingNode==null) return null;
Node<T> greater = startingNode.greater;
while (greater!=null && greater.id!=null) {
Node<T> node = greater.greater;
if (node!=null && node.id!=null) greater = node;
else break;
}
return greater;
}
/**
* Get least node in sub-tree rooted at startingNode. The
* search does not include startingNode in it's results.
*
* @param startingNode Root of tree to search.
* @return Node<T> which represents the least node in the
* startingNode sub-tree or NULL if startingNode has no lesser
* children.
*/
protected Node<T> getLeast(Node<T> startingNode) {
if (startingNode==null) return null;
Node<T> lesser = startingNode.lesser;
while (lesser!=null && lesser.id!=null) {
Node<T> node = lesser.lesser;
if (node!=null && node.id!=null) lesser = node;
else break;
}
return lesser;
}
/**
* Remove first occurrence of value in the tree.
*
* @param value T to remove from the tree.
* @return True if value was removed from the tree.
*/
public boolean remove(T value) {
Node<T> nodeToRemove = this.removeValue(value);
return (nodeToRemove!=null);
}
/**
* Remove first occurrence of value in the tree.
*
* @param value T to remove from the tree.
* @return Node<T> which was removed from the tree.
*/
protected Node<T> removeValue(T value) {
Node<T> nodeToRemoved = this.getNode(value);
if (nodeToRemoved != null) {
Node<T> replacementNode = this.getReplacementNode(nodeToRemoved);
replaceNodeWithNode(nodeToRemoved,replacementNode);
}
return nodeToRemoved;
}
/**
* Get the proper replacement node according to the binary
* search tree algorithm from the tree.
*
* @param nodeToRemoved Node<T> to find a replacement for.
* @return Node<T> which can be used to replace nodeToRemoved.
* nodeToRemoved should NOT be NULL.
*/
protected Node<T> getReplacementNode(Node<T> nodeToRemoved) {
Node<T> replacement = null;
Node<T> parent = nodeToRemoved.parent;
if (parent == null) {
// Replacing the root node
if (nodeToRemoved.lesser != null && nodeToRemoved.greater == null) {
// Replace with lesser subtree
replacement = nodeToRemoved.lesser;
} else if (nodeToRemoved.greater != null && nodeToRemoved.lesser==null) {
// Replace with greater subtree
replacement = nodeToRemoved.greater;
} else if (nodeToRemoved.greater != null && nodeToRemoved.lesser!=null) {
//Two children
replacement = this.getLeast(nodeToRemoved.greater);
if (replacement==null) replacement = nodeToRemoved.greater;
}
} else if (parent.lesser != null && (parent.lesser.id.compareTo(nodeToRemoved.id) == 0)) {
// If the node to remove is the parent's lesser node, replace
// the parent's lesser node with one of the node to remove's
// lesser/greater subtrees
if (nodeToRemoved.lesser != null && nodeToRemoved.greater == null) {
// Using the less subtree
replacement = nodeToRemoved.lesser;
} else if (nodeToRemoved.greater != null && nodeToRemoved.lesser == null) {
// Using the greater subtree (there is no lesser subtree, no refactoring)
replacement = nodeToRemoved.greater;
} else if (nodeToRemoved.greater != null && nodeToRemoved.lesser!=null) {
//Two children
replacement = this.getLeast(nodeToRemoved.greater);
if (replacement==null) replacement = nodeToRemoved.greater;
}
} else if (parent.greater != null && (parent.greater.id.compareTo(nodeToRemoved.id) == 0)) {
// If the node to remove is the parent's greater node, replace
// the parent's greater node with the node's greater node
if (nodeToRemoved.lesser != null && nodeToRemoved.greater == null) {
// Using the less subtree
replacement = nodeToRemoved.lesser;
} else if (nodeToRemoved.greater != null && nodeToRemoved.lesser == null) {
// Using the greater subtree (there is no lesser subtree, no refactoring)
replacement = nodeToRemoved.greater;
} else if (nodeToRemoved.greater != null && nodeToRemoved.lesser!=null) {
//Two children - use either the greatest child in the lesser branch or the least child in the greater branch
//Add some randomness to deletions, so we don't always use the greatest/least on deletion
if (modifications%2!=0) {
replacement = this.getGreatest(nodeToRemoved.lesser);
if (replacement==null) replacement = nodeToRemoved.lesser;
} else {
replacement = this.getLeast(nodeToRemoved.greater);
if (replacement==null) replacement = nodeToRemoved.greater;
}
modifications++;
}
}
return replacement;
}
/**
* Replace nodeToRemoved with replacementNode in the tree.
*
* @param nodeToRemoved Node<T> to remove replace in the tree. nodeToRemoved
* should NOT be NULL.
* @param replacementNode Node<T> to replace nodeToRemoved in the tree. replacementNode
* can be NULL.
*/
protected void replaceNodeWithNode(Node<T> nodeToRemoved, Node<T> replacementNode) {
if (replacementNode!=null) {
//Save for later
Node<T> replacementNodeLesser = replacementNode.lesser;
Node<T> replacementNodeGreater = replacementNode.greater;
//Replace replacementNode's branches with nodeToRemove's branches
Node<T> nodeToRemoveLesser = nodeToRemoved.lesser;
if (nodeToRemoveLesser!=null && !nodeToRemoveLesser.equals(replacementNode)) {
replacementNode.lesser = nodeToRemoveLesser;
nodeToRemoveLesser.parent = replacementNode;
}
Node<T> nodeToRemoveGreater = nodeToRemoved.greater;
if (nodeToRemoveGreater!=null && !nodeToRemoveGreater.equals(replacementNode)) {
replacementNode.greater = nodeToRemoveGreater;
nodeToRemoveGreater.parent = replacementNode;
}
//Remove link from replacementNode's parent to replacement
Node<T> replacementParent = replacementNode.parent;
if (replacementParent!=null && !replacementParent.equals(nodeToRemoved)) {
Node<T> replacementParentLesser = replacementParent.lesser;
Node<T> replacementParentGreater = replacementParent.greater;
if (replacementParentLesser!=null && replacementParentLesser.equals(replacementNode)) {
replacementParent.lesser = replacementNodeGreater;
if (replacementNodeGreater!=null) replacementNodeGreater.parent = replacementParent;
} else if (replacementParentGreater!=null && replacementParentGreater.equals(replacementNode)) {
replacementParent.greater = replacementNodeLesser;
if (replacementNodeLesser!=null) replacementNodeLesser.parent = replacementParent;
}
}
}
//Update the link in the tree from the nodeToRemoved to the replacementNode
Node<T> parent = nodeToRemoved.parent;
if (parent == null) {
// Replacing the root node
root = replacementNode;
if (root!=null) root.parent = null;
} else if (parent.lesser != null && (parent.lesser.id.compareTo(nodeToRemoved.id) == 0)) {
parent.lesser = replacementNode;
if (replacementNode!=null) replacementNode.parent = parent;
} else if (parent.greater != null && (parent.greater.id.compareTo(nodeToRemoved.id) == 0)) {
parent.greater = replacementNode;
if (replacementNode!=null) replacementNode.parent = parent;
}
size--;
}
/**
* Get number of nodes in the tree.
*
* @return Number of nodes in the tree.
*/
public int size() {
return size;
}
/**
* Validate the tree for all Binary Search Tree invariants.
*
* @return True if tree is valid.
*/
public boolean validate() {
if (root==null) return true;
return validateNode(root);
}
/**
* Validate the node for all Binary Search Tree invariants.
*
* @param node Node<T> to validate in the tree. node should
* NOT be NULL.
* @return True if the node is valid.
*/
protected boolean validateNode(Node<T> node) {
Node<T> lesser = node.lesser;
Node<T> greater = node.greater;
boolean lesserCheck = true;
if (lesser!=null && lesser.id!=null) {
lesserCheck = (lesser.id.compareTo(node.id) <= 0);
if (lesserCheck) lesserCheck = validateNode(lesser);
}
if (!lesserCheck) return false;
boolean greaterCheck = true;
if (greater!=null && greater.id!=null) {
greaterCheck = (greater.id.compareTo(node.id) > 0);
if (greaterCheck) greaterCheck = validateNode(greater);
}
return greaterCheck;
}
/**
* Get an array representation of the tree in breath first search order.
*
* @return breath first search sorted array representing the tree.
*/
@SuppressWarnings("unchecked")
public T[] getBFS() {
Queue<Node<T>> queue = new ArrayDeque<Node<T>>();
T[] values = (T[]) new Comparable[size];
int count = 0;
Node<T> node = root;
while (node!=null) {
values[count++] = node.id;
if (node.lesser!=null) queue.add(node.lesser);
if (node.greater!=null) queue.add(node.greater);
if (!queue.isEmpty()) node = queue.remove();
else node = null;
}
return values;
}
/**
* Get an array representation of the tree in depth first search order.
*
* @return depth first search sorted array representing the tree.
*/
@SuppressWarnings("unchecked")
public T[] getDFS() {
List<Node<T>> added = new ArrayList<Node<T>>(2);
T[] nodes = (T[]) new Comparable[size];
int index = 0;
Node<T> node = root;
while (index < size && node != null) {
Node<T> parent = node.parent;
Node<T> lesser = (node.lesser != null && !added.contains(node.lesser)) ? node.lesser : null;
Node<T> greater = (node.greater != null && !added.contains(node.greater)) ? node.greater : null;
if (parent == null && lesser == null && greater == null) {
if (!added.contains(node)) nodes[index++] = node.id;
break;
}
if (lesser != null) {
node = lesser;
} else {
if (!added.contains(node)) {
nodes[index++] = node.id;
added.add(node);
}
if (greater != null) {
node = greater;
} else if (greater == null && added.contains(node)) {
node = parent;
} else {
// We should not get here. Stop the loop!
node = null;
}
}
}
return nodes;
}
/**
* Get an array representation of the tree in sorted order.
*
* @return sorted array representing the tree.
*/
public T[] getSorted() {
// Depth first search to traverse the tree in order.
return getDFS();
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return TreePrinter.getString(this);
}
protected static class Node<T extends Comparable<T>> {
protected T id = null;
protected Node<T> parent = null;
protected Node<T> lesser = null;
protected Node<T> greater = null;
/**
* Node constructor.
*
* @param parent Parent link in tree. parent can be NULL.
* @param id T representing the node in the tree.
*/
protected Node(Node<T> parent, T id) {
this.parent = parent;
this.id = id;
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return "id =" + id +
" parent=" + ((parent != null) ? parent.id : "NULL") +
" lesser=" + ((lesser != null) ? lesser.id : "NULL") +
" greater=" + ((greater != null) ? greater.id : "NULL");
}
}
protected static interface INodeCreator<T extends Comparable<T>> {
/**
* Create a new Node with the following parameters.
*
* @param parent of this node.
* @param id of this node.
* @return new Node
*/
public Node<T> createNewNode(Node<T> parent, T id);
}
protected static class TreePrinter {
public static <T extends Comparable<T>> String getString(BinarySearchTree<T> tree) {
if (tree.root == null) return "Tree has no nodes.";
return getString(tree.root, "", true);
}
private static <T extends Comparable<T>> String getString(Node<T> node, String prefix, boolean isTail) {
StringBuilder builder = new StringBuilder();
if (node.parent!=null) {
String side = "left";
if (node.equals(node.parent.greater)) side = "right";
builder.append(prefix + (isTail ? "└── " : "├── ") + "(" + side + ") " + node.id + "\n");
} else {
builder.append(prefix + (isTail ? "└── " : "├── ") + node.id + "\n");
}
List<Node<T>> children = null;
if (node.lesser != null || node.greater != null) {
children = new ArrayList<Node<T>>(2);
if (node.lesser != null) children.add(node.lesser);
if (node.greater != null) children.add(node.greater);
}
if (children != null) {
for (int i = 0; i < children.size() - 1; i++) {
builder.append(getString(children.get(i), prefix + (isTail ? " " : "│ "), false));
}
if (children.size() >= 1) {
builder.append(getString(children.get(children.size() - 1), prefix + (isTail ? " " : "│ "), true));
}
}
return builder.toString();
}
}
}
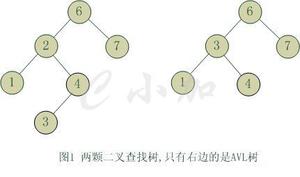
二叉树" title="平衡二叉树">平衡二叉树,AVL树,比较复杂了,需要对旋转
package com.jwetherell.algorithms.data_structures;import java.util.ArrayList;
import java.util.List;
/**
* An AVL tree is a self-balancing binary search tree, and it was the first such data
* structure to be invented. In an AVL tree, the heights of the two child subtrees
* of any node differ by at most one. AVL trees are often compared with red-black trees
* because they support the same set of operations and because red-black trees also take
* O(log n) time for the basic operations. Because AVL trees are more rigidly balanced,
* they are faster than red-black trees for lookup intensive applications. However,
* red-black trees are faster for insertion and removal.
*
* http://en.wikipedia.org/wiki/AVL_tree
*
* @author Justin Wetherell <phishman3579@gmail.com>
*/
public class AVLTree<T extends Comparable<T>> extends BinarySearchTree<T> implements BinarySearchTree.INodeCreator<T> {
private enum Balance { LEFT_LEFT, LEFT_RIGHT, RIGHT_LEFT, RIGHT_RIGHT };
/**
* Default constructor.
*/
public AVLTree() {
this.creator = this;
}
/**
* Constructor with external Node creator.
*/
public AVLTree(INodeCreator<T> creator) {
super(creator);
}
/**
* {@inheritDoc}
*/
@Override
protected Node<T> addValue(T id) {
Node<T> nodeToReturn = super.addValue(id);
AVLNode<T> nodeAdded = (AVLNode<T>) nodeToReturn;
while (nodeAdded!=null) {
nodeAdded.updateHeight();
balanceAfterInsert(nodeAdded);
nodeAdded = (AVLNode<T>) nodeAdded.parent;
}
return nodeToReturn;
}
/**
* Balance the tree according to the AVL post-insert algorithm.
*
* @param node Root of tree to balance.
*/
private void balanceAfterInsert(AVLNode<T> node) {
AVLNode<T> grandParent = (AVLNode<T>) node;
int balanceFactor = grandParent.getBalanceFactor();
if (balanceFactor>1 || balanceFactor<-1) {
AVLNode<T> parent = null;
AVLNode<T> child = null;
Balance balance = null;
if (balanceFactor<0) {
parent = (AVLNode<T>) grandParent.lesser;
balanceFactor = parent.getBalanceFactor();
if (balanceFactor<0) {
child = (AVLNode<T>) parent.lesser;
balance = Balance.LEFT_LEFT;
} else {
child = (AVLNode<T>) parent.greater;
balance = Balance.LEFT_RIGHT;
}
} else {
parent = (AVLNode<T>) grandParent.greater;
balanceFactor = parent.getBalanceFactor();
if (balanceFactor<0) {
child = (AVLNode<T>) parent.lesser;
balance = Balance.RIGHT_LEFT;
} else {
child = (AVLNode<T>) parent.greater;
balance = Balance.RIGHT_RIGHT;
}
}
if (balance == Balance.LEFT_RIGHT) {
//Left-Right (Left rotation, right rotation)
rotateLeft(parent);
rotateRight(grandParent);
} else if (balance == Balance.RIGHT_LEFT) {
//Right-Left (Right rotation, left rotation)
rotateRight(parent);
rotateLeft(grandParent);
} else if (balance == Balance.LEFT_LEFT) {
//Left-Left (Right rotation)
rotateRight(grandParent);
} else {
//Right-Right (Left rotation)
rotateLeft(grandParent);
}
grandParent.updateHeight(); //New child node
child.updateHeight(); //New child node
parent.updateHeight(); //New Parent node
}
}
/**
* {@inheritDoc}
*/
@Override
protected Node<T> removeValue(T value) {
//Find node to remove
Node<T> nodeToRemoved = this.getNode(value);
if (nodeToRemoved != null) {
//Find the replacement node
Node<T> replacementNode = this.getReplacementNode(nodeToRemoved);
//Find the parent of the replacement node to re-factor the height/balance of the tree
AVLNode<T> nodeToRefactor = null;
if (replacementNode!=null) nodeToRefactor = (AVLNode<T>) replacementNode.parent;
if (nodeToRefactor==null) nodeToRefactor = (AVLNode<T>) nodeToRemoved.parent;
if (nodeToRefactor!=null && nodeToRefactor.equals(nodeToRemoved)) nodeToRefactor = (AVLNode<T>) replacementNode;
//Replace the node
replaceNodeWithNode(nodeToRemoved,replacementNode);
//Re-balance the tree all the way up the tree
if (nodeToRefactor!=null) {
while (nodeToRefactor!=null) {
nodeToRefactor.updateHeight();
balanceAfterDelete(nodeToRefactor);
nodeToRefactor = (AVLNode<T>) nodeToRefactor.parent;
}
}
}
return nodeToRemoved;
}
/**
* Balance the tree according to the AVL post-delete algorithm.
*
* @param node Root of tree to balance.
*/
private void balanceAfterDelete(AVLNode<T> node) {
int balanceFactor = node.getBalanceFactor();
if (balanceFactor==-2 || balanceFactor==2) {
if (balanceFactor==-2) {
AVLNode<T> ll = (AVLNode<T>) node.lesser.lesser;
int lesser = (ll!=null)?ll.height:0;
AVLNode<T> lr = (AVLNode<T>) node.lesser.greater;
int greater = (lr!=null)?lr.height:0;
if (lesser>=greater) {
rotateRight(node);
node.updateHeight();
if (node.parent!=null) ((AVLNode<T>)node.parent).updateHeight();
} else {
rotateLeft(node.lesser);
rotateRight(node);
AVLNode<T> p = (AVLNode<T>) node.parent;
if (p.lesser!=null) ((AVLNode<T>)p.lesser).updateHeight();
if (p.greater!=null) ((AVLNode<T>)p.greater).updateHeight();
p.updateHeight();
}
} else if (balanceFactor==2) {
AVLNode<T> rr = (AVLNode<T>) node.greater.greater;
int greater = (rr!=null)?rr.height:0;
AVLNode<T> rl = (AVLNode<T>) node.greater.lesser;
int lesser = (rl!=null)?rl.height:0;
if (greater>=lesser) {
rotateLeft(node);
node.updateHeight();
if (node.parent!=null) ((AVLNode<T>)node.parent).updateHeight();
} else {
rotateRight(node.greater);
rotateLeft(node);
AVLNode<T> p = (AVLNode<T>) node.parent;
if (p.lesser!=null) ((AVLNode<T>)p.lesser).updateHeight();
if (p.greater!=null) ((AVLNode<T>)p.greater).updateHeight();
p.updateHeight();
}
}
}
}
/**
* {@inheritDoc}
*/
@Override
protected boolean validateNode(Node<T> node) {
boolean bst = super.validateNode(node);
if (!bst) return false;
AVLNode<T> avlNode = (AVLNode<T>) node;
int balanceFactor = avlNode.getBalanceFactor();
if (balanceFactor>1 || balanceFactor<-1) {
return false;
}
if (avlNode.isLeaf()) {
if (avlNode.height!=1) return false;
} else {
AVLNode<T> avlNodeLesser = (AVLNode<T>) avlNode.lesser;
int lesserHeight = 1;
if (avlNodeLesser!=null) lesserHeight = avlNodeLesser.height;
AVLNode<T> avlNodeGreater = (AVLNode<T>) avlNode.greater;
int greaterHeight = 1;
if (avlNodeGreater!=null) greaterHeight = avlNodeGreater.height;
if (avlNode.height==(lesserHeight+1) || avlNode.height==(greaterHeight+1)) {
return true;
} else {
return false;
}
}
return true;
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return AVLTreePrinter.getString(this);
}
/**
* {@inheritDoc}
*/
@Override
public Node<T> createNewNode(Node<T> parent, T id) {
return (new AVLNode<T>(parent,id));
}
protected static class AVLNode<T extends Comparable<T>> extends Node<T> {
protected int height = 1;
/**
* Constructor for an AVL node
*
* @param parent Parent of the node in the tree, can be NULL.
* @param value Value of the node in the tree.
*/
protected AVLNode(Node<T> parent, T value) {
super(parent,value);
}
/**
* Determines is this node is a leaf (has no children).
*
* @return True if this node is a leaf.
*/
protected boolean isLeaf() {
return ((lesser == null) && (greater == null));
}
/**
* Updates the height of this node based on it's children.
*/
protected void updateHeight() {
int lesserHeight = 0;
int greaterHeight = 0;
if (lesser != null) {
AVLNode<T> lesserAVLNode = (AVLNode<T>) lesser;
lesserHeight = lesserAVLNode.height;
}
if (greater != null) {
AVLNode<T> greaterAVLNode = (AVLNode<T>) greater;
greaterHeight = greaterAVLNode.height;
}
if (lesserHeight>greaterHeight) {
height = lesserHeight+1;
} else {
height = greaterHeight+1;
}
}
/**
* Get the balance factor for this node.
*
* @return An integer representing the balance factor for this node. It will be
* negative if the lesser branch is longer than the greater branch.
*/
protected int getBalanceFactor() {
int lesserHeight = 0;
int greaterHeight = 0;
if (lesser != null) {
AVLNode<T> lesserAVLNode = (AVLNode<T>) lesser;
lesserHeight = lesserAVLNode.height;
}
if (greater != null) {
AVLNode<T> greaterAVLNode = (AVLNode<T>) greater;
greaterHeight = greaterAVLNode.height;
}
return greaterHeight-lesserHeight;
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return "value=" + id +
" height=" + height +
" parent=" + ((parent != null) ? parent.id : "NULL") +
" lesser=" + ((lesser != null) ? lesser.id : "NULL") +
" greater=" + ((greater != null) ? greater.id : "NULL");
}
}
protected static class AVLTreePrinter {
public static <T extends Comparable<T>> String getString(AVLTree<T> tree) {
if (tree.root == null) return "Tree has no nodes.";
return getString((AVLNode<T>)tree.root, "", true);
}
public static <T extends Comparable<T>> String getString(AVLNode<T> node) {
if (node == null) return "Sub-tree has no nodes.";
return getString(node, "", true);
}
private static <T extends Comparable<T>> String getString(AVLNode<T> node, String prefix, boolean isTail) {
StringBuilder builder = new StringBuilder();
builder.append(prefix + (isTail ? "└── " : "├── ") + "(" + node.height + ") " + node.id + "\n");
List<Node<T>> children = null;
if (node.lesser != null || node.greater != null) {
children = new ArrayList<Node<T>>(2);
if (node.lesser != null) children.add(node.lesser);
if (node.greater != null) children.add(node.greater);
}
if (children != null) {
for (int i = 0; i < children.size() - 1; i++) {
builder.append(getString((AVLNode<T>)children.get(i), prefix + (isTail ? " " : "│ "), false));
}
if (children.size() >= 1) {
builder.append(getString((AVLNode<T>)children.get(children.size() - 1), prefix + (isTail ? " " : "│ "), true));
}
}
return builder.toString();
}
}
}
BTree 2-3树,分裂和合并部分还是比较简单的
import java.util.Arrays;import java.util.Comparator;
/**
* B-tree is a tree data structure that keeps data sorted and allows searches,
* sequential access, insertions, and deletions in logarithmic time. The B-tree
* is a generalization of a binary search tree in that a node can have more than
* two children. Unlike self-balancing binary search trees, the B-tree is
* optimized for systems that read and write large blocks of data. It is
* commonly used in databases and file-systems.
*
* http://en.wikipedia.org/wiki/B-tree
*
* @author Justin Wetherell <phishman3579@gmail.com>
*/
public class BTree<T extends Comparable<T>> {
// Default to 2-3 Tree
private int minKeySize = 1;
private int minChildrenSize = minKeySize + 1; //2
private int maxKeySize = 2 * minKeySize; //2
private int maxChildrenSize = maxKeySize + 1; //3
private Node<T> root = null;
private int size = 0;
/**
* Constructor for B-Tree which defaults to a 2-3 B-Tree.
*/
public BTree() { }
/**
* Constructor for B-Tree of ordered parameter.
*
* @param order of the B-Tree.
*/
public BTree(int order) {
this.minKeySize = order;
this.minChildrenSize = minKeySize + 1;
this.maxKeySize = 2 * minKeySize;
this.maxChildrenSize = maxKeySize + 1;
}
/**
* Add value to the tree. Tree can NOT contain multiple equal values.
*
* @param value T to add to the tree.
* @return True if successfully added to tree.
*/
public void add(T value) {
if (root == null) {
root = new Node<T>(null, maxKeySize, maxChildrenSize);
root.addKey(value);
} else {
Node<T> node = root;
while (node != null) {
if (node.numberOfChildren() == 0) {
node.addKey(value);
if (node.numberOfKeys() <= maxKeySize) {
// A-OK
break;
} else {
// Need to split up
split(node);
break;
}
} else {
// navigate
T lesser = node.getKey(0);
if (value.compareTo(lesser) < 0) {
node = node.getChild(0);
continue;
}
int size = node.numberOfKeys();
int last = size - 1;
T greater = node.getKey(last);
if (value.compareTo(greater) > 0) {
node = node.getChild(size);
continue;
}
for (int i = 1; i < node.numberOfKeys(); i++) {
T prev = node.getKey(i - 1);
T next = node.getKey(i);
if (value.compareTo(prev) > 0 && value.compareTo(next) < 0) {
node = node.getChild(i);
break;
}
}
}
}
}
size++;
}
/**
* The node's key size is greater than maxKeySize, split down the middle.
*
* @param node to split.
*/
private void split(Node<T> node) {
int size = node.numberOfKeys();
int medianIndex = size / 2;
T medianValue = node.getKey(medianIndex);
Node<T> left = new Node<T>(null, maxKeySize, maxChildrenSize);
for (int i=0; i<medianIndex; i++) {
left.addKey(node.getKey(i));
}
if (node.numberOfChildren()>0) {
for (int j=0; j<=medianIndex; j++) {
Node<T> c = node.getChild(j);
left.addChild(c);
}
}
Node<T> right = new Node<T>(null, maxKeySize, maxChildrenSize);
for (int i = medianIndex+1; i < size; i++) {
right.addKey(node.getKey(i));
}
if (node.numberOfChildren()>0) {
for (int j=medianIndex+1; j<node.numberOfChildren(); j++) {
Node<T> c = node.getChild(j);
right.addChild(c);
}
}
if (node.parent == null) {
// new root, height of tree is increased
Node<T> newRoot = new Node<T>(null, maxKeySize, maxChildrenSize);
newRoot.addKey(medianValue);
node.parent = newRoot;
root = newRoot;
node = root;
node.addChild(left);
node.addChild(right);
} else {
// Move the median value up to the parent
Node<T> parent = node.parent;
parent.addKey(medianValue);
parent.removeChild(node);
parent.addChild(left);
parent.addChild(right);
if (parent.numberOfKeys() > maxKeySize) split(parent);
}
}
/**
* Does the tree contain the value.
*
* @param value T to locate in the tree.
* @return True if tree contains value.
*/
public boolean contains(T value) {
Node<T> node = getNode(value);
return (node != null);
}
/**
* Get the node with value.
*
* @param value to find in the tree.
* @return Node<T> with value.
*/
private Node<T> getNode(T value) {
Node<T> node = root;
while (node != null) {
T lesser = node.getKey(0);
if (value.compareTo(lesser) < 0) {
if (node.numberOfChildren() > 0) node = node.getChild(0);
else node = null;
continue;
}
int size = node.numberOfKeys();
int last = size - 1;
T greater = node.getKey(last);
if (value.compareTo(greater) > 0) {
if (node.numberOfChildren() > size) node = node.getChild(size);
else node = null;
continue;
}
for (int i = 0; i < size; i++) {
T currentValue = node.getKey(i);
if (currentValue.compareTo(value) == 0) {
return node;
}
int next = i + 1;
if (next <= last) {
T nextValue = node.getKey(next);
if (currentValue.compareTo(value) < 0 && nextValue.compareTo(value) > 0) {
if (next < node.numberOfChildren()) {
node = node.getChild(next);
break;
} else {
return null;
}
}
}
}
}
return null;
}
/**
* Remove the value from the tree.
*
* @param value T to remove from the tree.
* @return True if value was removed from the tree.
*/
public boolean remove(T value) {
Node<T> node = this.getNode(value);
if (node == null) return false;
int index = node.indexOf(value);
node.removeKey(value);
if (node.numberOfChildren()==0) {
//leaf node
if (node.parent!=null && node.numberOfKeys() < minKeySize) {
this.combined(node);
} else if (node.parent==null && node.numberOfKeys()==0) {
//Removing root node with no keys or children
root = null;
}
} else {
//internal node
Node<T> lesser = node.getChild(index);
Node<T> greatest = this.getGreatestNode(lesser);
T replaceValue = this.removeGreatestValue(greatest);
node.addKey(replaceValue);
if (greatest.parent!=null && greatest.numberOfKeys() < minKeySize) {
this.combined(greatest);
}
if (greatest.numberOfChildren() > maxChildrenSize) {
this.split(greatest);
}
}
size--;
return true;
}
/**
* Remove greatest valued key from node.
*
* @param node to remove greatest value from.
* @return value removed;
*/
private T removeGreatestValue(Node<T> node) {
T value = null;
if (node.numberOfKeys()>0) {
value = node.removeKey(node.numberOfKeys()-1);
}
return value;
}
/**
* Get the greatest valued child from node.
*
* @param node child with the greatest value.
* @return Node<T> child with greatest value.
*/
private Node<T> getGreatestNode(Node<T> node) {
while (node.numberOfChildren()>0) {
node = node.getChild(node.numberOfChildren()-1);
}
return node;
}
/**
* Combined children keys with parent when size is less than minKeySize.
*
* @param node with children to combined.
* @return True if combined successfully.
*/
private boolean combined(Node<T> node) {
Node<T> parent = node.parent;
int index = parent.indexOf(node);
int indexOfLeftNeighbor = index - 1;
int indexOfRightNeighbor = index + 1;
Node<T> rightNeighbor = null;
int rightNeighborSize = -minChildrenSize;
if (indexOfRightNeighbor < parent.numberOfChildren()) {
rightNeighbor = parent.getChild(indexOfRightNeighbor);
rightNeighborSize = rightNeighbor.numberOfKeys();
}
// Try to borrow neighbor
if (rightNeighbor != null && rightNeighborSize > minKeySize) {
// Try to borrow from right neighbor
T removeValue = rightNeighbor.getKey(0);
int prev = getIndexOfPreviousValue(parent, removeValue);
T parentValue = parent.removeKey(prev);
T neighborValue = rightNeighbor.removeKey(0);
node.addKey(parentValue);
parent.addKey(neighborValue);
if (rightNeighbor.numberOfChildren()>0) {
node.addChild(rightNeighbor.removeChild(0));
}
} else {
Node<T> leftNeighbor = null;
int leftNeighborSize = -minChildrenSize;
if (indexOfLeftNeighbor >= 0) {
leftNeighbor = parent.getChild(indexOfLeftNeighbor);
leftNeighborSize = leftNeighbor.numberOfKeys();
}
if (leftNeighbor != null && leftNeighborSize > minKeySize) {
// Try to borrow from left neighbor
T removeValue = leftNeighbor.getKey(leftNeighbor.numberOfKeys() - 1);
int prev = getIndexOfNextValue(parent, removeValue);
T parentValue = parent.removeKey(prev);
T neighborValue = leftNeighbor.removeKey(leftNeighbor.numberOfKeys() - 1);
node.addKey(parentValue);
parent.addKey(neighborValue);
if (leftNeighbor.numberOfChildren()>0) {
node.addChild(leftNeighbor.removeChild(leftNeighbor.numberOfChildren()-1));
}
} else if (rightNeighbor != null && parent.numberOfKeys() > 0) {
// Can't borrow from neighbors, try to combined with right neighbor
T removeValue = rightNeighbor.getKey(0);
int prev = getIndexOfPreviousValue(parent, removeValue);
T parentValue = parent.removeKey(prev);
parent.removeChild(rightNeighbor);
node.addKey(parentValue);
for (int i=0; i<rightNeighbor.keysSize; i++) {
T v = rightNeighbor.getKey(i);
node.addKey(v);
}
for (int i=0; i<rightNeighbor.childrenSize; i++) {
Node<T> c = rightNeighbor.getChild(i);
node.addChild(c);
}
if (parent.parent != null && parent.numberOfKeys() < minKeySize) {
// removing key made parent too small, combined up tree
this.combined(parent);
} else if (parent.numberOfKeys() == 0) {
// parent no longer has keys, make this node the new root
// which decreases the height of the tree
node.parent = null;
root = node;
}
} else if (leftNeighbor != null && parent.numberOfKeys() > 0) {
// Can't borrow from neighbors, try to combined with left neighbor
T removeValue = leftNeighbor.getKey(leftNeighbor.numberOfKeys() - 1);
int prev = getIndexOfNextValue(parent, removeValue);
T parentValue = parent.removeKey(prev);
parent.removeChild(leftNeighbor);
node.addKey(parentValue);
for (int i=0; i<leftNeighbor.keysSize; i++) {
T v = leftNeighbor.getKey(i);
node.addKey(v);
}
for (int i=0; i<leftNeighbor.childrenSize; i++) {
Node<T> c = leftNeighbor.getChild(i);
node.addChild(c);
}
if (parent.parent != null && parent.numberOfKeys() < minKeySize) {
// removing key made parent too small, combined up tree
this.combined(parent);
} else if (parent.numberOfKeys() == 0) {
// parent no longer has keys, make this node the new root
// which decreases the height of the tree
node.parent = null;
root = node;
}
}
}
return true;
}
/**
* Get the index of previous key in node.
*
* @param node to find the previous key in.
* @param value to find a previous value for.
* @return index of previous key or -1 if not found.
*/
private int getIndexOfPreviousValue(Node<T> node, T value) {
for (int i = 1; i < node.numberOfKeys(); i++) {
T t = node.getKey(i);
if (t.compareTo(value) >= 0) return i - 1;
}
return node.numberOfKeys() - 1;
}
/**
* Get the index of next key in node.
*
* @param node to find the next key in.
* @param value to find a next value for.
* @return index of next key or -1 if not found.
*/
private int getIndexOfNextValue(Node<T> node, T value) {
for (int i = 0; i < node.numberOfKeys(); i++) {
T t = node.getKey(i);
if (t.compareTo(value) >= 0) return i;
}
return node.numberOfKeys() - 1;
}
/**
* Get number of nodes in the tree.
*
* @return Number of nodes in the tree.
*/
public int size() {
return size;
}
/**
* Validate the tree for all B-Tree invariants.
*
* @return True if tree is valid.
*/
public boolean validate() {
if (root == null) return true;
return validateNode(root);
}
/**
* Validate the node according to the B-Tree invariants.
*
* @param node to validate.
* @return True if valid.
*/
private boolean validateNode(Node<T> node) {
int keySize = node.numberOfKeys();
if (keySize > 1) {
// Make sure the keys are sorted
for (int i = 1; i < keySize; i++) {
T p = node.getKey(i - 1);
T n = node.getKey(i);
if (p.compareTo(n) > 0) return false;
}
}
int childrenSize = node.numberOfChildren();
if (node.parent == null) {
//root
if (keySize > maxKeySize) {
// check max key size. root does not have a min key size
return false;
} else if (childrenSize==0) {
// if root, no children, and keys are valid
return true;
} else if (childrenSize < 2) {
// root should have zero or at least two children
return false;
} else if (childrenSize > maxChildrenSize) {
return false;
}
} else {
//non-root
if (keySize < minKeySize) {
return false;
} else if (keySize > maxKeySize) {
return false;
} else if (childrenSize==0) {
return true;
} else if (keySize != (childrenSize - 1)) {
// If there are chilren, there should be one more child then keys
return false;
} else if (childrenSize < minChildrenSize) {
return false;
} else if (childrenSize > maxChildrenSize) {
return false;
}
}
Node<T> first = node.getChild(0);
// The first child's last key should be less than the node's first key
if (first.getKey(first.numberOfKeys() - 1).compareTo(node.getKey(0)) > 0) return false;
Node<T> last = node.getChild(node.numberOfChildren() - 1);
// The last child's first key should be greater than the node's last key
if (last.getKey(0).compareTo(node.getKey(node.numberOfKeys() - 1)) < 0) return false;
// Check that each node's first and last key holds it's invariance
for (int i = 1; i < node.numberOfKeys(); i++) {
T p = node.getKey(i - 1);
T n = node.getKey(i);
Node<T> c = node.getChild(i);
if (p.compareTo(c.getKey(0)) > 0) return false;
if (n.compareTo(c.getKey(c.numberOfKeys() - 1)) < 0) return false;
}
for (int i=0; i<node.childrenSize; i++) {
Node<T> c = node.getChild(i);
boolean valid = this.validateNode(c);
if (!valid) return false;
}
return true;
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return TreePrinter.getString(this);
}
private static class Node<T extends Comparable<T>> {
private T[] keys = null;
private int keysSize = 0;
private Node<T>[] children = null;
private int childrenSize = 0;
private Comparator<Node<T>> comparator = new Comparator<Node<T>>() {
@Override
public int compare(Node<T> arg0, Node<T> arg1) {
return arg0.getKey(0).compareTo(arg1.getKey(0));
}
};
protected Node<T> parent = null;
@SuppressWarnings("unchecked")
private Node(Node<T> parent, int maxKeySize, int maxChildrenSize) {
this.parent = parent;
this.keys = (T[]) new Comparable[maxKeySize+1];
this.keysSize = 0;
this.children = new Node[maxChildrenSize+1];
this.childrenSize = 0;
}
private T getKey(int index) {
return keys[index];
}
private int indexOf(T value) {
for (int i=0; i<keysSize; i++) {
if (keys[i].equals(value)) return i;
}
return -1;
}
private void addKey(T value) {
keys[keysSize++] = value;
Arrays.sort(keys,0,keysSize);
}
private boolean removeKey(T value) {
boolean found = false;
if (keysSize==0) return found;
for (int i=0; i<keysSize; i++) {
if (keys[i].equals(value)) {
found = true;
} else if (found) {
//shift the rest of the keys down
keys[i-1] = keys[i];
}
}
if (found) {
keysSize--;
keys[keysSize] = null;
}
return found;
}
private T removeKey(int index) {
if (index>=keysSize) return null;
T value = keys[index];
keys[index] = null;
for (int i=index+1; i<keysSize; i++) {
//shift the rest of the keys down
keys[i-1] = keys[i];
}
keysSize--;
keys[keysSize] = null;
return value;
}
private int numberOfKeys() {
return keysSize;
}
private Node<T> getChild(int index) {
if (index>=childrenSize) return null;
return children[index];
}
private int indexOf(Node<T> child) {
for (int i=0; i<childrenSize; i++) {
if (children[i].equals(child)) return i;
}
return -1;
}
private boolean addChild(Node<T> child) {
child.parent = this;
children[childrenSize++] = child;
Arrays.sort(children,0,childrenSize,comparator);
return true;
}
private boolean removeChild(Node<T> child) {
boolean found = false;
if (childrenSize==0) return found;
for (int i=0; i<childrenSize; i++) {
if (children[i].equals(child)) {
found = true;
} else if (found) {
//shift the rest of the keys down
children[i-1] = children[i];
}
}
if (found) {
childrenSize--;
children[childrenSize] = null;
}
return found;
}
private Node<T> removeChild(int index) {
if (index>=childrenSize) return null;
Node<T> value = children[index];
children[index] = null;
for (int i=index+1; i<childrenSize; i++) {
//shift the rest of the keys down
children[i-1] = children[i];
}
childrenSize--;
children[childrenSize] = null;
return value;
}
private int numberOfChildren() {
return childrenSize;
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
builder.append("keys=[");
for (int i = 0; i < numberOfKeys(); i++) {
T value = getKey(i);
builder.append(value);
if (i < numberOfKeys() - 1) builder.append(", ");
}
builder.append("]\n");
if (parent != null) {
builder.append("parent=[");
for (int i = 0; i < parent.numberOfKeys(); i++) {
T value = parent.getKey(i);
builder.append(value);
if (i < parent.numberOfKeys() - 1) builder.append(", ");
}
builder.append("]\n");
}
if (children != null) {
builder.append("children=").append(numberOfChildren()).append("\n");
}
return builder.toString();
}
}
private static class TreePrinter {
public static <T extends Comparable<T>> String getString(BTree<T> tree) {
if (tree.root == null) return "Tree has no nodes.";
return getString(tree.root, "", true);
}
private static <T extends Comparable<T>> String getString(Node<T> node, String prefix, boolean isTail) {
StringBuilder builder = new StringBuilder();
builder.append(prefix).append((isTail ? "└── " : "├── "));
for (int i = 0; i < node.numberOfKeys(); i++) {
T value = node.getKey(i);
builder.append(value);
if (i < node.numberOfKeys() - 1) builder.append(", ");
}
builder.append("\n");
if (node.children != null) {
for (int i = 0; i < node.numberOfChildren() - 1; i++) {
Node<T> obj = node.getChild(i);
builder.append(getString(obj, prefix + (isTail ? " " : "│ "), false));
}
if (node.numberOfChildren() >= 1) {
Node<T> obj = node.getChild(node.numberOfChildren() - 1);
builder.append(getString(obj, prefix + (isTail ? " " : "│ "), true));
}
}
return builder.toString();
}
}
}
二叉堆,最简单的树结构实现了
import java.util.ArrayList;import java.util.Arrays;
import java.util.List;
/**
* A binary heap is a heap data structure created using a binary tree. It can be
* seen as a binary tree with two additional constraints: 1) The shape property:
* the tree is a complete binary tree; that is, all levels of the tree, except
* possibly the last one (deepest) are fully filled, and, if the last level of
* the tree is not complete, the nodes of that level are filled from left to
* right. 2) The heap property: each node is right than or equal to each of its
* children according to a comparison predicate defined for the data structure.
*
* http://en.wikipedia.org/wiki/Binary_heap
*
* @author Justin Wetherell <phishman3579@gmail.com>
*/
public abstract class BinaryHeap<T extends Comparable<T>> {
public enum HeapType { Tree, Array };
public enum Type { MIN, MAX };
/**
* Number of nodes in the heap.
*
* @return Number of nodes in the heap.
*/
public abstract int size();
/**
* Add value to the heap.
*
* @param value to add to the heap.
*/
public abstract void add(T value);
/**
* Does the value exist in the heap. Warning
* this is a O(n) operation.
*
* @param value to locate in the heap.
* @return True if the value is in heap.
*/
public abstract boolean contains(T value);
/**
* Get the heap in array form.
*
* @return array representing the heap.
*/
public abstract T[] getHeap();
/**
* Get the value of the head node from the heap.
*
* @return value of the head node.
*/
public abstract T getHeadValue();
/**
* Remove the head node from the heap.
*
* @return value of the head node.
*/
public abstract T removeHead();
/**
* Validate the heap according to the invariants.
*
* @return True if the heap is valid.
*/
public abstract boolean validate();
public static <T extends Comparable<T>> BinaryHeap<T> createHeap(HeapType type) {
switch (type) {
case Array:
return new BinaryHeapArray<T>();
default:
return new BinaryHeapTree<T>();
}
}
/**
* A binary heap using an array to hold the nodes.
*
* @author Justin Wetherell <phishman3579@gmail.com>
*/
public static class BinaryHeapArray<T extends Comparable<T>> extends BinaryHeap<T> {
private static final int MINIMUM_SIZE = 10;
private Type type = Type.MIN;
private int size = 0;
@SuppressWarnings("unchecked")
private T[] array = (T[]) new Comparable[MINIMUM_SIZE];
/**
* Get the parent index of this index, will return Integer.MIN_VALUE if no parent
* is possible.
*
* @param index of the node to find a parent for.
* @return index of parent node or Integer.MIN_VALUE if no parent.
*/
private static final int getParentIndex(int index) {
if (index>0) return (int) Math.floor((index-1)/2);
else return Integer.MIN_VALUE;
}
/**
* Get the left child index of this index.
*
* @param index of the node to find a left child for.
* @return index of left child node.
*/
private static final int getLeftIndex(int index) {
return 2*index+1;
}
/**
* Get the right child index of this index.
*
* @param index of the node to find a right child for.
* @return index of right child node.
*/
private static final int getRightIndex(int index) {
return 2*index+2;
}
/**
* Constructor for heap, defaults to a min-heap.
*/
public BinaryHeapArray() {
size = 0;
}
/**
* Constructor for heap.
*
* @param type Heap type.
*/
public BinaryHeapArray(Type type) {
this();
this.type = type;
}
/**
* {@inheritDoc}
*/
@Override
public int size() {
return size;
}
/**
* {@inheritDoc}
*/
@Override
public void add(T value) {
if (size>=array.length) {
array = Arrays.copyOf(array, ((size*3)/2)+1);
}
array[size] = value;
heapUp(size++);
}
protected void heapUp(int nodeIndex) {
T value = this.array[nodeIndex];
while (nodeIndex>=0) {
int parentIndex = getParentIndex(nodeIndex);
if (parentIndex<0) break;
T parent = this.array[parentIndex];
if ( (type == Type.MIN && parent != null && value.compareTo(parent) < 0) ||
(type == Type.MAX && parent != null && value.compareTo(parent) > 0)
){
// Node is less than parent, switch node with parent
this.array[parentIndex] = value;
this.array[nodeIndex] = parent;
} else {
nodeIndex = parentIndex;
}
}
}
/**
* {@inheritDoc}
*/
@Override
public boolean contains(T value) {
if (array.length==0) return false;
for (int i=0; i<size; i++) {
T node = array[i];
if (node.equals(value)) return true;
}
return false;
}
/**
* {@inheritDoc}
*/
@Override
public boolean validate() {
if (array.length==0) return true;
return validateNode(0);
}
/**
* Validate the node for the heap invariants.
*
* @param node to validate for.
* @return True if node is valid.
*/
private boolean validateNode(int index) {
T value = this.array[index];
int leftIndex = getLeftIndex(index);
int rightIndex = getRightIndex(index);
//We shouldn't ever have a right node without a left in a heap
if (rightIndex!=Integer.MIN_VALUE && leftIndex==Integer.MIN_VALUE) return false;
if (leftIndex!=Integer.MIN_VALUE && leftIndex<size) {
T left = this.array[leftIndex];
if ((type == Type.MIN && value.compareTo(left) < 0) || (type == Type.MAX && value.compareTo(left) > 0)) {
return validateNode(leftIndex);
} else {
return false;
}
}
if (rightIndex!=Integer.MIN_VALUE && rightIndex<size) {
T right = this.array[rightIndex];
if ((type == Type.MIN && value.compareTo(right) < 0) || (type == Type.MAX && value.compareTo(right) > 0)) {
return validateNode(rightIndex);
} else {
return false;
}
}
return true;
}
/**
* {@inheritDoc}
*/
@Override
@SuppressWarnings("unchecked")
public T[] getHeap() {
T[] nodes = (T[]) new Comparable[size];
if (array.length==0) return nodes;
for (int i=0; i<size; i++) {
T node = this.array[i];
nodes[i] = node;
}
return nodes;
}
/**
* {@inheritDoc}
*/
@Override
public T getHeadValue() {
if (array.length==0) return null;
return array[0];
}
/**
* {@inheritDoc}
*/
@Override
public T removeHead() {
T result = null;
if (array.length==0) return result;
//Get the root element in the array
result = array[0];
//Save the last element of the array and then null out the last element's index
int lastIndex = --size;
T lastNode = array[lastIndex];
array[size] = null;
//No more elements in the heap
if (size<=0) {
return result;
}
//Put the last element in the root's spot
array[0] = lastNode;
if (size>=MINIMUM_SIZE && size<array.length/2) {
array = Arrays.copyOf(array, size);
}
//Heap down from the root
heapDown(0);
return result;
}
protected void heapDown(int index) {
T value = this.array[index];
int leftIndex = getLeftIndex(index);
int rightIndex = getRightIndex(index);
T left = (leftIndex!=Integer.MIN_VALUE && leftIndex<this.size)?this.array[leftIndex]:null;
T right = (rightIndex!=Integer.MIN_VALUE && rightIndex<this.size)?this.array[rightIndex]:null;
if (left == null && right == null) {
// Nothing to do here
return;
}
T nodeToMove = null;
int nodeToMoveIndex = -1;
if ( (type == Type.MIN && left != null && right != null && value.compareTo(left) > 0 && value.compareTo(right) > 0) ||
(type == Type.MAX && left != null && right != null && value.compareTo(left) < 0 && value.compareTo(right) < 0)
) {
// Both children are greater/lesser than node
if ((type == Type.MIN && right.compareTo(left) < 0) ||
(type == Type.MAX && right.compareTo(left) > 0)
) {
// Right is greater/lesser than left
nodeToMove = right;
nodeToMoveIndex = rightIndex;
} else if ( (type == Type.MIN && left.compareTo(right) < 0) ||
(type == Type.MAX && left.compareTo(right) > 0)
){
// Left is greater/lesser than right
nodeToMove = left;
nodeToMoveIndex = leftIndex;
} else {
// Both children are equal, use right
nodeToMove = right;
nodeToMoveIndex = rightIndex;
}
} else if ( (type == Type.MIN && right != null && value.compareTo(right) > 0) ||
(type == Type.MAX && right != null && value.compareTo(right) < 0)
) {
// Right is greater/lesser than node
nodeToMove = right;
nodeToMoveIndex = rightIndex;
} else if ( (type == Type.MIN && left != null && value.compareTo(left) > 0) ||
(type == Type.MAX && left != null && value.compareTo(left) < 0)
) {
// Left is greater/lesser than node
nodeToMove = left;
nodeToMoveIndex = leftIndex;
}
// No node to move, stop recursion
if (nodeToMove == null) return;
// Re-factor heap sub-tree
this.array[nodeToMoveIndex] = value;
this.array[index] = nodeToMove;
heapDown(nodeToMoveIndex);
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return HeapPrinter.getString(this);
}
protected static class HeapPrinter {
public static <T extends Comparable<T>> String getString(BinaryHeapArray<T> tree) {
if (tree.array.length==0) return "Tree has no nodes.";
T root = tree.array[0];
if (root == null) return "Tree has no nodes.";
return getString(tree, 0, "", true);
}
private static <T extends Comparable<T>> String getString(BinaryHeapArray<T> tree, int index, String prefix, boolean isTail) {
StringBuilder builder = new StringBuilder();
T value = tree.array[index];
builder.append(prefix + (isTail ? "└── " : "├── ") + value + "\n");
List<Integer> children = null;
int leftIndex = getLeftIndex(index);
int rightIndex = getRightIndex(index);
if (leftIndex != Integer.MIN_VALUE || rightIndex != Integer.MIN_VALUE) {
children = new ArrayList<Integer>(2);
if (leftIndex != Integer.MIN_VALUE && leftIndex<tree.size) {
children.add(leftIndex);
}
if (rightIndex != Integer.MIN_VALUE && rightIndex<tree.size) {
children.add(rightIndex);
}
}
if (children != null) {
for (int i = 0; i < children.size() - 1; i++) {
builder.append(getString(tree, children.get(i), prefix + (isTail ? " " : "│ "), false));
}
if (children.size() >= 1) {
builder.append(getString(tree, children.get(children.size() - 1), prefix + (isTail ? " " : "│ "), true));
}
}
return builder.toString();
}
}
}
public static class BinaryHeapTree<T extends Comparable<T>> extends BinaryHeap<T> {
private Type type = Type.MIN;
private int size = 0;
private Node<T> root = null;
/**
* Constructor for heap, defaults to a min-heap.
*/
public BinaryHeapTree() {
root = null;
size = 0;
}
/**
* Constructor for heap.
*
* @param type Heap type.
*/
public BinaryHeapTree(Type type) {
this();
this.type = type;
}
/**
* {@inheritDoc}
*/
@Override
public int size() {
return size;
}
/**
* Get the navigation directions through the tree to the index.
*
* @param index of the Node to get directions for.
* @return Integer array representing the directions to the index.
*/
private int[] getDirections(int index) {
int directionsSize = (int) (Math.log10(index + 1) / Math.log10(2)) - 1;
int[] directions = null;
if (directionsSize > 0) {
directions = new int[directionsSize];
int i = directionsSize - 1;
while (i >= 0) {
index = (index - 1) / 2;
directions[i--] = (index > 0 && index % 2 == 0) ? 1 : 0; // 0=left,
// 1=right
}
}
return directions;
}
/**
* {@inheritDoc}
*/
@Override
public void add(T value) {
add(new Node<T>(null, value));
}
private void add(Node<T> newNode) {
if (root == null) {
root = newNode;
size++;
return;
}
Node<T> node = root;
int[] directions = getDirections(size); // size == index of new node
if (directions != null && directions.length > 0) {
for (int d : directions) {
if (d == 0) {
// Go left
node = node.left;
} else {
// Go right
node = node.right;
}
}
}
if (node.left == null) {
node.left = newNode;
} else {
node.right = newNode;
}
newNode.parent = node;
size++;
heapUp(newNode);
}
/**
* Remove the root node.
*/
private void removeRoot() {
// Find the last node
int[] directions = getDirections(size - 1); // Directions to the last node
Node<T> lastNode = root;
if (directions != null && directions.length > 0) {
for (int d : directions) {
if (d == 0) {
// Go left
lastNode = lastNode.left;
} else {
// Go right
lastNode = lastNode.right;
}
}
}
Node<T> lastNodeParent = null;
if (lastNode.right != null) {
lastNodeParent = lastNode;
lastNode = lastNode.right;
lastNodeParent.right = null;
} else if (lastNode.left != null) {
lastNodeParent = lastNode;
lastNode = lastNode.left;
lastNodeParent.left = null;
}
lastNode.left = root.left;
if (lastNode.left != null) lastNode.left.parent = lastNode;
lastNode.right = root.right;
if (lastNode.right != null) lastNode.right.parent = lastNode;
lastNode.parent = null;
if (!lastNode.equals(root)) root = lastNode;
else root = null;
size--;
heapDown(lastNode);
}
/**
* Get the node in the startingNode sub-tree which has the value.
*
* @param startingNode node rooted sub-tree to search in.
* @param value to search for.
* @return Node<T> which equals value in sub-tree or NULL if not found.
*/
private Node<T> getNode(Node<T> startingNode, T value) {
Node<T> result = null;
if (startingNode != null && startingNode.value.equals(value)) {
result = startingNode;
} else if (startingNode != null && !startingNode.value.equals(value)) {
Node<T> left = startingNode.left;
if (left != null) {
result = getNode(left, value);
if (result != null) return result;
}
Node<T> right = startingNode.right;
if (right != null) {
result = getNode(right, value);
if (result != null) return result;
}
}
return result;
}
/**
* {@inheritDoc}
*/
@Override
public boolean contains(T value) {
if (root==null) return false;
Node<T> node = getNode(root, value);
return (node!=null);
}
/**
* Heap up the heap from this node.
*
* @param node to heap up.
*/
protected void heapUp(Node<T> node) {
while (node != null) {
Node<T> heapNode = (Node<T>) node;
Node<T> parent = heapNode.parent;
if ( (type == Type.MIN && parent != null && node.value.compareTo(parent.value) < 0) ||
(type == Type.MAX && parent != null && node.value.compareTo(parent.value) > 0)
){
// Node is less than parent, switch node with parent
Node<T> grandParent = parent.parent;
Node<T> parentLeft = parent.left;
Node<T> parentRight = parent.right;
parent.left = heapNode.left;
if (parent.left != null) parent.left.parent = parent;
parent.right = heapNode.right;
if (parent.right != null) parent.right.parent = parent;
if (parentLeft != null && parentLeft.equals(node)) {
heapNode.left = parent;
heapNode.right = parentRight;
if (parentRight != null) parentRight.parent = heapNode;
} else {
heapNode.right = parent;
heapNode.left = parentLeft;
if (parentLeft != null) parentLeft.parent = heapNode;
}
parent.parent = heapNode;
if (grandParent == null) {
// New root.
heapNode.parent = null;
root = heapNode;
} else {
Node<T> grandLeft = grandParent.left;
if (grandLeft != null && grandLeft.equals(parent)) {
grandParent.left = heapNode;
} else {
grandParent.right = heapNode;
}
heapNode.parent = grandParent;
}
} else {
node = heapNode.parent;
}
}
}
/**
* Heap down the heap from this node.
*
* @param node to heap down.
*/
protected void heapDown(Node<T> node) {
Node<T> heapNode = (Node<T>) node;
Node<T> left = heapNode.left;
Node<T> right = heapNode.right;
if (left == null && right == null) {
// Nothing to do here
return;
}
Node<T> nodeToMove = null;
if ( (type == Type.MIN && left != null && right != null && node.value.compareTo(left.value) > 0 && node.value.compareTo(right.value) > 0) ||
(type == Type.MAX && left != null && right != null && node.value.compareTo(left.value) < 0 && node.value.compareTo(right.value) < 0)
) {
// Both children are greater/lesser than node
if ((type == Type.MIN && right.value.compareTo(left.value) < 0) ||
(type == Type.MAX && right.value.compareTo(left.value) > 0)
) {
// Right is greater/lesser than left
nodeToMove = right;
} else if ( (type == Type.MIN && left.value.compareTo(right.value) < 0) ||
(type == Type.MAX && left.value.compareTo(right.value) > 0)
){
// Left is greater/lesser than right
nodeToMove = left;
} else {
// Both children are equal, use right
nodeToMove = right;
}
} else if ( (type == Type.MIN && right != null && node.value.compareTo(right.value) > 0) ||
(type == Type.MAX && right != null && node.value.compareTo(right.value) < 0)
) {
// Right is greater than node
nodeToMove = right;
} else if ( (type == Type.MIN && left != null && node.value.compareTo(left.value) > 0) ||
(type == Type.MAX && left != null && node.value.compareTo(left.value) < 0)
) {
// Left is greater than node
nodeToMove = left;
}
// No node to move, stop recursion
if (nodeToMove == null) return;
// Re-factor heap sub-tree
Node<T> nodeParent = heapNode.parent;
if (nodeParent == null) {
// heap down the root
root = nodeToMove;
root.parent = null;
Node<T> nodeToMoveLeft = nodeToMove.left;
Node<T> nodeToMoveRight = nodeToMove.right;
if (heapNode.left.equals(nodeToMove)) {
nodeToMove.left = heapNode;
nodeToMove.right = heapNode.right;
} else {
nodeToMove.left = heapNode.left;
nodeToMove.right = heapNode;
}
heapNode.parent = nodeToMove;
heapNode.left = nodeToMoveLeft;
heapNode.right = nodeToMoveRight;
} else {
// heap down a left
if (nodeParent.left.equals(node)) {
nodeParent.left = nodeToMove;
nodeToMove.parent = nodeParent;
} else {
nodeParent.right = nodeToMove;
nodeToMove.parent = nodeParent;
}
Node<T> nodeLeft = heapNode.left;
Node<T> nodeRight = heapNode.right;
Node<T> nodeToMoveLeft = nodeToMove.left;
Node<T> nodeToMoveRight = nodeToMove.right;
if (heapNode.left.equals(nodeToMove)) {
nodeToMove.right = nodeRight;
if (nodeRight != null) nodeRight.parent = nodeToMove;
nodeToMove.left = heapNode;
heapNode.parent = nodeToMove;
} else {
nodeToMove.left = nodeLeft;
if (nodeLeft != null) nodeLeft.parent = nodeToMove;
nodeToMove.right = heapNode;
heapNode.parent = nodeToMove;
}
heapNode.left = nodeToMoveLeft;
if (nodeToMoveLeft != null) nodeToMoveLeft.parent = heapNode;
heapNode.right = nodeToMoveRight;
if (nodeToMoveRight != null) nodeToMoveRight.parent = heapNode;
}
heapDown(node);
}
/**
* {@inheritDoc}
*/
@Override
public boolean validate() {
if (root==null) return true;
return validateNode(root);
}
/**
* Validate node for heap invariants.
*
* @param node to validate for.
* @return True if node is valid.
*/
private boolean validateNode(Node<T> node) {
Node<T> left = ((Node<T>)node).left;
Node<T> right = ((Node<T>)node).right;
//We shouldn't ever have a right node without a left in a heap
if (right!=null && left==null) return false;
if (left!=null) {
if ((type == Type.MIN && node.value.compareTo(left.value) < 0) || (type == Type.MAX && node.value.compareTo(left.value) > 0)) {
return validateNode(left);
} else {
return false;
}
}
if (right!=null) {
if ((type == Type.MIN && node.value.compareTo(right.value) < 0) || (type == Type.MAX && node.value.compareTo(right.value) > 0)) {
return validateNode(right);
} else {
return false;
}
}
return true;
}
/**
* Populate the node in the array at the index.
*
* @param node to populate.
* @param index of node in array.
* @param array where the node lives.
*/
private void getNodeValue(Node<T> node, int index, T[] array) {
array[index] = node.value;
index = (index * 2) + 1;
Node<T> left = ((Node<T>)node).left;
if (left != null) getNodeValue(left, index, array);
Node<T> right = ((Node<T>)node).right;
if (right != null) getNodeValue(right, index + 1, array);
}
/**
* {@inheritDoc}
*/
@Override
@SuppressWarnings("unchecked")
public T[] getHeap() {
T[] nodes = (T[]) new Comparable[size];
if (root != null) getNodeValue(root, 0, nodes);
return nodes;
}
/**
* {@inheritDoc}
*/
@Override
public T getHeadValue() {
T result = null;
if (root != null) result = root.value;
return result;
}
/**
* {@inheritDoc}
*/
@Override
public T removeHead() {
T result = null;
if (root != null) {
result = root.value;
removeRoot();
}
return result;
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return HeapPrinter.getString(this);
}
protected static class HeapPrinter {
public static <T extends Comparable<T>> void print(BinaryHeapTree<T> tree) {
System.out.println(getString(tree.root, "", true));
}
public static <T extends Comparable<T>> String getString(BinaryHeapTree<T> tree) {
if (tree.root == null) return "Tree has no nodes.";
return getString(tree.root, "", true);
}
private static <T extends Comparable<T>> String getString(Node<T> node, String prefix, boolean isTail) {
StringBuilder builder = new StringBuilder();
builder.append(prefix + (isTail ? "└── " : "├── ") + node.value + "\n");
List<Node<T>> children = null;
if (node.left != null || node.right != null) {
children = new ArrayList<Node<T>>(2);
if (node.left != null) children.add(node.left);
if (node.right != null) children.add(node.right);
}
if (children != null) {
for (int i = 0; i < children.size() - 1; i++) {
builder.append(getString(children.get(i), prefix + (isTail ? " " : "│ "), false));
}
if (children.size() >= 1) {
builder.append(getString(children.get(children.size() - 1), prefix + (isTail ? " " : "│ "), true));
}
}
return builder.toString();
}
}
private static class Node<T extends Comparable<T>> {
private T value = null;
private Node<T> parent = null;
private Node<T> left = null;
private Node<T> right = null;
private Node(Node<T> parent, T value) {
this.value = value;
this.parent = parent;
}
/**
* {@inheritDoc}
*/
@Override
public String toString() {
return "value=" + value +
" parent=" + ((parent != null) ? parent.value : "NULL") +
" left=" + ((left != null) ? left.value : "NULL") +
" right=" + ((right != null) ? right.value : "NULL");
}
}
}
}
后续把学习完的数据结构的其他树结构再贴出来。
以上是 java 关于二叉搜索树,平衡二叉树,b树,二叉堆的几段代码 的全部内容, 来源链接: utcz.com/z/390981.html