Java实现红黑树(平衡二叉树)的详细过程
前言
在实现红黑树之前,我们先来了解一下符号表。
符号表的描述借鉴了Algorithms第四版,详情在:https://algs4.cs.princeton.edu/home/
符号表有时候被称为字典,就如同英语字典中,一个单词对应一个解释,符号表有时候又被称之为索引,即书本最后将术语按照字母顺序列出以方便查找的那部分。总的来说,符号表就是将一个键和一个值联系起来,就如Python中的字典,JAVA中的HashMap和HashTable,Redis中以键值对的存储方式。
在如今的大数据时代,符号表的使用是非常频繁的,但在一个拥有着海量数据的符号表中,如何去实现快速的查找以及插入数据就是高效的算法去完成的事情,可以说没有这些算法的发明产生,信息时代无从谈起。
既然是数据结构去实现符号表,这就要求我们对符号表的API,也就是符号表的功能去定义,前面我们说到既然符号表的使用是如何在海量数据中去查找,插入数据,那么我们便定义符号表的API有增删改查这四个基本功能。
/**
* <p>
* 符号表的基本API
* </p>
* @author qzlzzz
* @version 1.0
* @since 2021/10/8
*/
public interface RedBlackBST<Key extends Comparable<Key>,Value> {
/**
* 根据Key在符号表中找到Value
* @param key the key
* @return the value of key
*/
Value get(Key key);
/**
* 插入key-value,如果符号表中有Key,且Key不为空则将该Key的Value转为传入的Value
* @param key the-key
* @param value the-value
*/
void put(Key key,Value value);
/**
* 根据Key去符号表中删除Key
* @param key the key
*/
void delete(Key key);
}
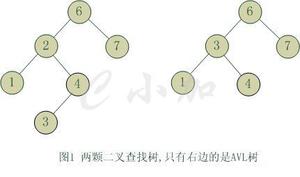
这里由于红黑树是平衡二叉树,即意味着其有平衡性和有序性,因为其有序性的特点,因此我们可以范围或根据位置去需找键,也可以查找到树中的最小键和最大键。
至于什么是平衡性,文章后讲,这里先停一停。
因此我们可以额外的定义:
/**
* 根据位置返回键,如果没有返回null
* @param k the index of key
* @return the key
*/
Key select(int k);
/**
* 返回红黑树中最小的键
* @return the min key in this tree
*/
Key min();
/**
* 返回红黑树中最大的键
* @return the max key in this tree
*/
Key max();
/**
* 返回小于该键的数量
* @param key the key
* @return amount of key small than the key
*/
int rank(Key key);
接下来我们说说红黑树。
红黑二叉查找树
红黑二叉查找树实际上基于二叉查找树上实现了2-3树,也就是说红黑二叉查找树是一个2-3树。所以在认识红黑二叉查找树之前,我们得了解2-3树的原理,以及组成结构。
2-3树
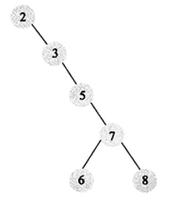
我们把含有一个键,两个链接的结点称为2-结点,标准的二叉查找树其每个结点都是2-结点,在考虑好的情况下,我们构造标准二叉查找树,一般能够得到树高为总键树的对数的一个查找树,其查找和插入操作都是对数级别的,但标准二叉查找树的基本实现的良好性能取决于键值对分布的足够乱以致于打消长路径带来的问题,但我们不能保证插入情况是随机的,如果键值对的插入时顺序插入的,就会带来下面的问题:
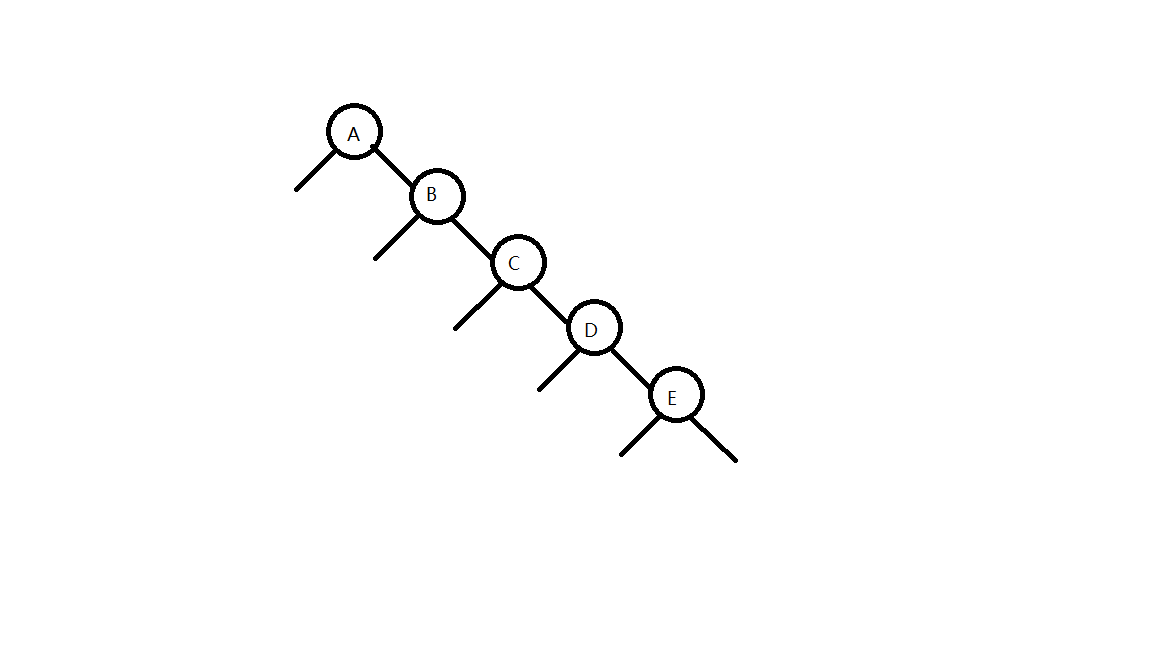
从图中我们可以看到,我们将A,B,C,D,E按顺序插入的话,会得到一个键值与树高成正比的二叉查找树,其插入和查找的会从对数级别提到O(N)级别。
当然我们希望的肯定是无论键值对的情况是怎样的,我们都能构造一个树高与总键数成对数,插入查找等操作均能够在对数时间内完成的数据结构。也就是说,在顺序插入的情况下,我们希望树高依然为~lgN,这样我们就能保证所有的查找都能在~lgN次比较结束。
为了保证查找树的平衡性,我们需要一些灵活性,因此在这里我们允许树中的一个结点保存多个键,我们引入3-结点,所谓的3-结点就是一个结点中有2个键,3个链接。
因此一颗2-3查找树或为一颗空树,或由2-结点和3-结点组成。在介绍2-3树的操作前,我们将A,B,C,D,E,F,G,H顺序插入得到的树如下图所示:

从图中我们可以看出2-3树的平衡性,灵活性,它保证了任意的插入得到的树高依旧是总键的对数。
2-3树的插入操作
理解2-3树的插入操作,有利于去构造红黑树,在这里分三种情况:
- 插入新键,底层结点是2-结点
- 插入新键,底层结点是3-结点,父结点是2-结点
- 插入新键,底层结点是3-结点,父结点是3-结点
第一种情况
若插入新键,底层结点是2-结点的话,该底层结点变为3-结点,将插入的键保存其中即可。

第二种情况
若插入新键,底层结点是3-结点,底层结点先变成临时的4-结点(3个键,4条链接),后4-结点中的中键吐出,使得父节点由2-结点变为3-结点,原4-结点中键两边的键变成两个2-结点,原本由父结点指向子结点的一个链接,替换为原4-结点中键左右两边的链接,分别指向两个新的2-结点。

第三种情况
若插入新键,底层结点是3-结点,其父结点也是3-结点的话,使得底层结点变为临时的4-结点,后4-结点中的中键吐出,使得父节点由3-结点变为临时的4-结点,原4-结点中键两边的键变成两个2-结点,原本由父结点指向子结点的一个链接,替换为原4-结点中键左右两边的链接,分别指向两个新的2-结点,随后父节点也要吐出中键,重复上述的步骤,如果父节点的父节点也是3-结点,则继续持续上述步骤,若根结点也是3-结点,根节点吐出中键,生成两个2-结点后,整个树高+1,但各个底层结点到根结点的路径始终相等。

以上的三种变化是2-3树的动态变化的核心,非常关键,我们可以在推演的过程种看到这种变化是自下向上的,而且是局部的变化,这种局部的变化并没有影响2-3树的有序性和平衡性。
同时我们也可以看出,如果要以代码来实现2-3树的话相当的麻烦,因为需要处理的情况实在太多。我们需要维护两种不同类型的结点,将被查找的键和结中的每个键进行比较,将链接和其他信息从一个结点复制到另一个结点。实现这些需要大量的代码,实现的这些代码所带来开销或许还会比标准二叉查找树要多。因此后面人们想出了结合标准二叉树来实现2-3树的数据结构,这便是红黑树。
实现红黑二叉树
红黑树是基于标准二叉树来实现的,它实现2-3树的关键点在于它把二叉树的链接分为了红和黑。它将两个用红链相链接的结点看为3-结点,而黑链链接的结点则视为2-结点。这也意味着我们完全不用去重新写一个红黑树的get()方法,只需要使用标准二叉树的get()方法就可以实现查找,不同点在于,要在put()方法中改动一下便能够去实现一个红黑二叉查找树。实现红黑树代码改动量少,但其后面的思想其实很复杂,由于篇幅的原因,对红黑树如何去实现2-3树的三种变化的原理就不做过多描述。
首先定义结点
/**
* <h3>
* 红黑树的实现,博客:https://www.cnblogs.com/qzlzzz/p/15395010.html
* </h3>
* @author qzlzzz
* @since 2021/10/12
* @version 1.0
*/
public class RedBlackBST<Key extends Comparable<Key>,Value> {
private Node root;//根节点
//<父结点>指向自己<子结点>的链接是黑色的
private static final boolean RED = true;
//<父结点>指向自己<子结点>的链接是黑色的
private static final boolean BLACK = false;
/**
* <p>红黑树的结点定义</p>
* @author qzlzzz
*/
private class Node{
private boolean color;//指向该结点的链接的颜色
private Key key;//键
private Value value;//值
private Node left,right;//该结点指向左结点的链接和右结点的链接
private int n;//该子树的结点树
public Node(Key key,Value value,boolean color,int n){
this.key = key;
this.value = value;
this.color = color;
this.n = n;
}
}
}
若红链接为右链接,使链接转左。
在这里我们需要保持红链接为左链接。但使红链接保持为右链接也行,只不过左链接更好实现。
/**
* 计算红黑树的结点总数,内部调用了{@link RedBlackBST#size(Node)}
* @return
*/
public int size(){
return size(root);
}
//计算某个子树的结点总数
private int size(Node x){
if (x == null) return 0;
else return x.n;
}
/**
* 将红色右链接变为左链接,总体有序性不变,子树结点数量不变
* @param h
* @return
*/
private Node rotateLeft(Node h){
Node t = h.right;
h.right = t.left;
t.left = h;
t.color = h.color;
h.color = RED;
t.n = h.n;//转换后子树的结点是不变的,
h.n = size(h.left) + size(h.right) + 1;
return t;
}
转换的代码图是这样的:

这里的1 2 3指的是键的大小,并不是值,红黑树各个底层到根节点的黑链接总数的相同的,这符合了2-3树中各个底层结点到根节点的距离相等。
这里将红左链接转换为右链接的思想是一样的,读者可以自己尝试去实现。
判断链接是否为红链接
//判断链接是否为红色,不是返回false
private boolean isRed(Node x){
if (x == null) return false;
return x.color;
}
若左右两边的链接皆为红色,将两边链接颜色设置为黑色,并使指向自己链接的颜色设为红
/**
* <p>若左右两边的链接皆为红色,将两边链接颜色设置为黑色,并使指向自己链接的颜色设为红</p>
* @param x
*/
private void changeColor(Node x){
x.color = true;
x.left.color = false;
x.right.color = true;
}
为什么要这样呢?
其实跟上述2-3树的第二个操作脱不开关系。当结点为临时4-结点时,吐出中键,两边的键变为两个2-结点,原指向临时4-结点的链接变为原4-结点中间两边的链接并指向新的2-结点,如果父结点为2-结点,则于原4-中键一起变成3-结点,若父节点是3-结点,则循环上述操作,由于我们要保持红链接为做链接,中途若有右红链接产生还需要使用rotateLeft()方法去转换。

接下来让我们以红黑二叉树实现符号表的get、put
/**
* 通过键来查找值,内部调用{@link RedBlackBST#get(Node, Comparable)}
* @param key
* @return
*/
public Value get(Key key){
if (key == null) throw new IllegalArgumentException("argument to get() is null");
return get(root,key);
}
private Value get(Node x,Key key){
for (;;){
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp == 0) return x.value;
else if (cmp < 0) x = x.left;
else x = x.right;
}
}
/**
* 插入键值对,内部使用{@link RedBlackBST#put(Node, Comparable, Object)}
* @param key
* @param value
*/
public void put(Key key,Value value){
if (key == null) throw new IllegalArgumentException("argument to put() is null");
root = put(root,key,value);
root.color = false;
}
private Node put(Node x,Key key,Value value){
if (x == null) return new Node(key,value,RED,1);
int cmp = key.compareTo(x.key);
if (cmp == 0) {x.value = value;}
else if (cmp < 0) x.left = put(x.left,key,value);
else x.right = put(x.right,key,value);
if (isRed(x.right) && !isRed(x.left)) x = rotateLeft(x);
if (isRed(x.left) && isRed(x.left.left)) x = rotateRight(x);
if (isRed(x.left) && isRed(x.right)) changeColor(x);
x.n = size(x.left) + size(x.right) + 1;
return x;
}
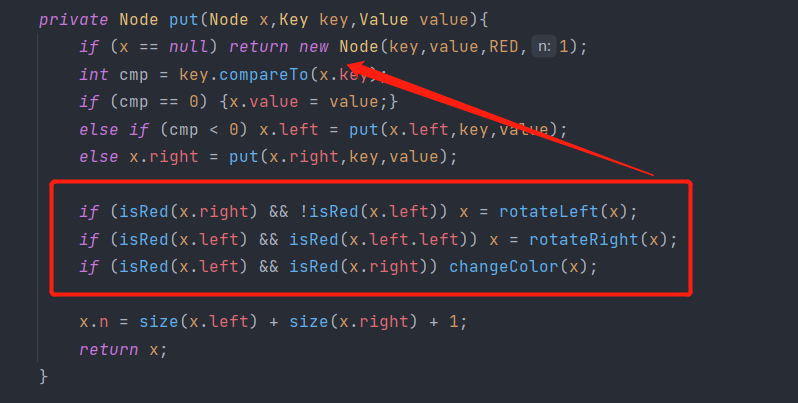
至于put方法,后面的三个if语句则是:
- 当前结点的右链接为红色的话,将其转为左红链接。当左右链接皆为红色,调用changeColor()方法,使得其完成2-3树的局部动态变化,也就是上述说的2-3树的插入新键,底层结点是3-结点,父结点是2-结点的操作。
- 当前结点的左链接,以及左链接的左连接都为红色的话,说明这是一个临时的4-结点,我们需要将第一个左红链接转为右红链接,然后得到一个左右链接都为红的子树,调用changeRed()方法使得其完成2-3树的局部动态变化,也就是上述说的2-3树的插入新键,底层结点是3-结点,父结点是2-结点的操作。
- 当左右链接都为红色,调用changeColor()方法。
最后实现符号表的rank,select
/**
* 根据位置返回键,内部调用{@link RedBlackBST#select(Node, int)}
* @param k
* @return
*/
public Key select(int k){
return select(root,k);
}
private Key select(Node x,int k){
while(x != null){
int t = x.left.N;
if (t > k) x = x.left;
else if (t < k){
x = x.right;
k = k - t - 1;
}
else return x.key;
}
return null;
}
/**
* 根据键,返回该键的数量,内部调用{@link RedBlackBST#rank(Node, Comparable)}
* @param key
* @return
*/
public int rank(Key key){
return rank(root,key);
}
private int rank(Node x,Key key){
while (x != null){
int cmp = key.compareTo(x.key);
int count = x.left.N;
if (cmp == 0) return (count < root.N ? count : 1 + root.left.N + count);
else if (cmp < 0) x = x.left;
else x = x.right;
}
return 0;
}
最后以红黑二叉树的符号表实现完成了,读者也可以尝试将put()方法中的后三个语句放在判断结点x为空的语句后面,有意思的是,此树会变成一个2-3-4树,也就说存在4-结点的一颗树。
结尾
感谢zsh帅哥,若本文有什么需要改进或不足的地方请联系我。
本文参考了:https://algs4.cs.princeton.edu/30searching/
到此这篇关于Java实现红黑树(平衡二叉树)的文章就介绍到这了,更多相关Java实现红黑树(平衡二叉树)内容请搜索以前的文章或继续浏览下面的相关文章希望大家以后多多支持!
以上是 Java实现红黑树(平衡二叉树)的详细过程 的全部内容, 来源链接: utcz.com/p/249790.html