算法漫游指北(第三篇):数据结构可视化网站、数组(列表)、链表、跳表、在python中实现链表

零、数据结构可视化网站
数据结构比较难于理解,自己画图又太慢,可以找一些数据结构可视化的网站帮助学习。
可视化的交互模式介绍数据结构和算法,非常有利于理解。
Data structure visualizations http://www.cs.usfca.edu/~galles/visualization/Algorithms.html
visualgo 部分中文 https://visualgo.net/zh
fmdca380 (国内的visualgo ?)全中文 http://ds.fmdca380.com/index.html
sorting http://sorting.at/
ps:以上网站如果打不开表示需要FQ
一、数组(列表)、链表、跳表
顺序表:python里的列表、c\java里的数组
数组(ArrayList)
java\c++写法:基础写法:int a[100];
每当我们申请数组的时候,计算机实际上是在内存中给我们开辟了一段连续的地址,每一个地址通过内存管理器进行访问。
直接访问时间复杂度都为O(1),它可以随机访问任何一个元素,所以它的访问时间非常快。
插入删除过程
在增加和删除数组元素的时候会进行一些相应的操作。 插入操作: 在插入D之前,我们要将EFG往下挪一个位置,把3号位置让出来,然后将D放进去。导致插入的操作不是常数级的,而是O(n)的复杂度。
同理,删除最后一个元素时间复杂度是O(1),
但是如果是删除中间或者前面的元素时间复杂度是O(n)。 在ArrayList中,如果超出数组长度,就会将数组长度扩增加一倍。
数组优点:
地址连续,访问任意一项都是常数级别O(1);
数组缺点:
删除,增加元素时间复杂度高,需要遍历,一般为O(n),插入前保证数组的size足够;
数组size较小,会进行扩容,拷贝等低效的操作。
数组的本质
数组的本质是把数据存储在计算机内存管理器开辟的连续内存地址对应的位置
所以数组的随机访问时间复杂度为O(1),搜索元素的时间复杂度为O(n)
插入删除元素由于平均需要移动半个数组的元素,平均时间复杂度为O(n)
列表(List)
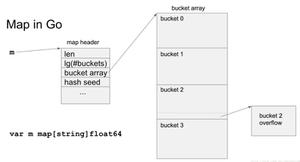
在Python中,列表是一个动态的指针数组,也是在内存中 以*连续的存储空间存储列表元素对象的内存地址,以偏移量计算取得元素*。
在python3中一起皆对象,在内存中实际是按照下图方式存储的:
存入列表的是这些对象的内存地址,不是值。列表本身也是对象,列表的内存地址传给了变量a。
在Python的官方实现中,list实现采用了如下的策略:在建立空表(或者很小的表)时,系统分配一块能容纳8个元素的存储区;在执行插入操作(insert或append)时,如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大(目前的阀值为50000),则改变策略,采用加一倍的方法。引入这种改变策略的方式,是为了避免出现过多空闲的存储位置。
数组与列表的比较
数组元素要类型相同
数组长度固定,而python的列表可以根据需要增加分配的内存,也就是可以增加列表的长度。
数组和列表在增加、插入、查询、删除的时间复杂度是一样的。
链表(Linked List)
在一些添加和删除操作比较频繁的情况下,我们经常会使用链表,改善时间复杂度。它所做的一件事情就是元素定义好之后,有所谓的value和next,next指向下一个元素,那么串在一起就变成了一个类似与数组的这么的一个结构。每一个元素用class定义,这个class一般叫做node。里面有两个成员变量,一个叫value(也可以是个类),一个next指针,指向下一个元素。
单链表图示
如果只有一个next指针,我们叫单链表;有的时候,我们需要往前指一个就叫它的prev或者previous,这个链表我们叫做双链表。即能往后面走,也能往前面走,同理,它的头指针叫head,尾指针叫tail来表示。最后一个元素,它的next指针指向空。另外一种情况是,如果tail指针的next也可以指回到head来,我们叫其为循环链表。
双链表结构图示
链表添加元素过程
首先,为这个新元素创造一个节点,我们叫做new node,在链表下发放好,假设,我们要插入第二个位置,我们要将前一个节点的next指向新节点,新元素的next指向原来的下一个节点,这样插入新元素就完成了。
链表删除元素过程
与添加类似,删除target node 是第一个node的next直接指向第三个node,跨过了要删除的节点,在内存中将target node节点释放掉,这样就完成了删除过程。
不管元素在什么位置,添加和删除只需要两次next指针的调整,就可以完成添加或者删除操作,所以这里的时间复杂度是O(1),要优于数组。但是有个问题,要查询某个元素,需要对链表从头到某个元素位置进行遍历查找,时间复杂度是O(n)。
链表优点:
灵活,插入不需要扩容、移动其他元素或者拷贝等操作,O(1);
链表缺点:
占用内存,32系统一个指针4字节;
遍历、查找不方便,必须挨个遍历,不能用下表访问,一般为O(n)。
链表时间复杂度总结
部分中英文对照lookup 查询
insert 插入
delete 删除
prepend 在链表最前面添加一个新的节点作为头节点
append 将新节点插入链表结尾
链表的本质是每个元素靠指针指向其相邻元素,随机访问需要遍历整个链表
访问和搜索的时间复杂度为O(n)
插入删除元素只需要处理相邻元素的指针指向关系,所以插入和删除的时间复杂度为O(1)
链表与数组比较
链表在插入和删除的操作上明显快于数组
链表的内存可以更灵活的分配
链表这种链式存储的数据结构对树和图的结构有很大的启发性
链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大,但对存储空间的使用要相对灵活。
链表与数组的各种操作复杂度如下所示:
注意虽然表面看起来复杂度都是 O(n),但是链表和数组在插入和删除时进行的是完全不同的操作。链表的主要耗时操作是遍历查找,删除和插入操作本身的复杂度是O(1)。数组查找很快,主要耗时的操作是拷贝覆盖。因为除了目标元素在尾部的特殊情况,数组进行插入和删除时需要对操作点之后的所有元素进行前后移位操作,只能通过拷贝和覆盖的方法进行。
跳表
跳表是为了优化或者是弥补链表的缺陷而设计的,跳表的本质是在链表的基础上进行升维,加入多级索引,每级索引不再是跳向相邻元素,而是跳跃 2^k 个元素,redis 的sorted set的底层实现就是跳表。
针对链表的优化思路:链表每次遍历的 粒度是一个元素,可不可能一次走两步、三步…
答案是肯定的。比如支持一次走两步的遍历方式
加速链表查询优化的中心思想
升维,或者叫做空间换时间。 简单优化:添加头尾指针。
再深入优化可以增加一级索引,增加所谓的中指针
查询的时候一级索引指针指向头指针这是第一个,它的下一个位置指向next+1的位置。索引基于链表,链表是走向next,索引的话每次向next+1也就是两倍的next。next的每次速度为1,一级索引每次速度为2.
当然,我们还可以再增加新的二级索引,让速度变得更快。
以此类推,我们可以增加多级索引。
但是这里时间复杂度也没有降到O(1),而是降到时间复杂度:O(logn)。
这样做多级索引的缺点:
维护成本高,增加删除都需要重新更新索引;
空间复杂度较高,O(n),需要
跳表在工程中的应用
LRU Cache - Linked list: LRU 缓存机制
Redis - Skip LIst
二、python中实现链表(一)
python 标准库并没有实现链表所以我们得自己实现链表。
单向链表
单向链表也叫单链表,是链表中最简单的一种形式,它的每个节点包含两个域,一个信息域(元素域)和一个链接域。这个链接指向链表中的下一个节点,而最后一个节点的链接域则指向一个空值。
单向链表由节点组成。
.每个节点包含两个域,元素域和链接域。元素域存放数据,链接域存放下一个节点的地址信息
表元素域data用来存放具体的数据
每个节点指向下一个节点,最后一个节点指向空
链接域next用来存放下一个节点的位置(python中的标识)
变量p指向链表的头节点(首节点)的位置,从p出发能找到表中的任意节点。
节点实现
class SingleNode(object):"""单链表的结点"""
def __init__(self,item):
# _item存放数据元素,初始化元素区
self.item = item
# _next是下一个节点的标识,初始化链接区,默认指向空
self.next = None
定义链表的一些属性及方法:
1.is_empty() # 判断链表为空
2.append(item) # 尾部添加元素
3.add(item) # 头部添加元素
4.insert(pos,item) # 指定位置添加元素
5.remove(item) # 删除节点
6.search(item) # 查找节点是否存在
7.travel() # 遍历链表
8.length() # 返回链表长度
未完待续,见下一篇博客...
参考资料
[1]深入python编程 (雨痕)
[2]https://blog.csdn.net/weixin_43790623/article/details/103036981
[3]https://redisbook.readthedocs.io/en/latest/internal-datastruct/skiplist.html
以上是 算法漫游指北(第三篇):数据结构可视化网站、数组(列表)、链表、跳表、在python中实现链表 的全部内容, 来源链接: utcz.com/z/388120.html