python求最大连续子数组的和
抛出问题:
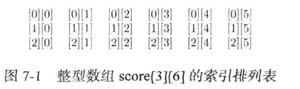
求一数组如 l = [0, 1, 2, 3, -4, 5, -6],求该数组的最大连续子数组的和 如结果为[0,1,2,3,-4,5] 的和为7
问题分析:
这个问题很简单,直接暴力法,上代码。
# -*- coding:utf-8 -*-
# 日期:2018/6/9 7:46
# Author:小鼠标
# 最大连续子数组的和
l = [0, 1, 2, 3, -4, 5, -6]
# 暴力求解
def violence(l = []):
maxVal = 0
x,y=0,0
for i in range(0,len(l)+1):
for j in range(0,len(l)+1):
res = sum(l[i:j])
if res > maxVal:
maxVal = res
x = i
y = j
return maxVal,x,y
maxVal, x, y = violence(l)
print(maxVal,(x,y))
分治法:
关键是暴力法的时间复杂度太高,所以就在原有的基础上做了进一步的提升--分治法。
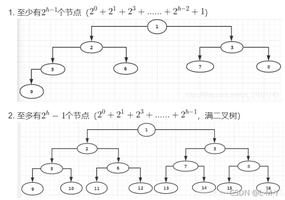
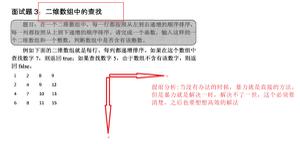
所谓分治法就是将原有的列表一分为二,那么最大的子列表只有三种情况:
1、最大子列表完全在左边
2、最大子列表完全在右边
3、最大子列表跨立在中间
所以我们分情况讨论,求出答案。这种方法一定程度的降低了时间复杂度,从之前的n^2降到了(n/2)^2 + 2n
# -*- coding:utf-8 -*-
# 日期:2018/6/9 7:46
# Author:小鼠标
# 最大连续子数组的和
l = [0, 1, 2, 3, -4, 5, -6]
#暴力求解
def violence(l = []):
maxVal = 0
x,y=0,0
for i in range(0,len(l)+1):
for j in range(0,len(l)+1):
res = sum(l[i:j])
if res > maxVal:
maxVal = res
x = i
y = j
return maxVal,x,y
#分治法 想左扫 向右扫,求出两边的最大值
def left_or_right(l):
maxVal = 0
term = 0
for i in l:
term += i
if maxVal < term:
maxVal = term
return maxVal
def Separate():
middle = int(len(l)/2)
l1 = l[0:middle]
l2 = l[middle:len(l)]
#左半部分
maxVal1,x1,y1 = violence(l1)
#右半部分
maxVal2,x2,y2 = violence(l2)
#跨立在中间
max_right = left_or_right(l2)
max_left = left_or_right(l1[::-1])
maxVal3 = max_right + max_left
return max(maxVal1,maxVal2,maxVal3)
val = Separate()
print(val)
动态规划:
即便是分治法,时间复杂度还是太高,不满足生产的需求,所以如果说只求最大子序列的和的值而不去追求最大子序列本身,我们又引出一个方法--动态规划
这种方法的时间复杂是是线性的,极大的降低了。
# -*- coding:utf-8 -*-
# 日期:2018/6/9 8:38
# Author:小鼠标
def function(lists):
max_sum = lists[0]
pre_sum = 0
for i in lists:
# 因为最大子列表一定是从一个非0的数开始的(假定列表中有正数有负数)
# 所以就可以暂时筛选调小于0的数,即便列表全是负数,那么最大的子列表肯定是负数最大的一个
if pre_sum < 0:
pre_sum = i
else:
pre_sum += i
if pre_sum > max_sum:
max_sum = pre_sum
return max_sum
lists = [0, 1, 2, 3, -4, 5, -6]
print(function(lists))
以上是 python求最大连续子数组的和 的全部内容, 来源链接: utcz.com/z/356607.html