图的深度优先搜索(DFS)
深度优先搜索(DFS)是一种图遍历算法。在该算法中,给出了一个起始顶点,当找到相邻顶点时,它将首先移动到该相邻顶点并尝试以相同的方式遍历。
它会在整个深度范围内进行尽可能多的移动,然后回溯到先前的顶点以查找新路径。
为了以迭代方式实现DFS,我们需要使用堆栈数据结构。如果我们要递归执行,则不需要外部堆栈,可以为递归调用完成内部堆栈。
输入输出
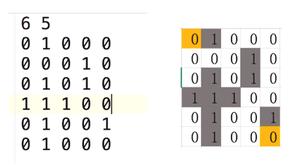
Input:The Adjacency matrix of a graph.
A B C D E F
A 0 1 1 1 0 0
B 1 0 0 1 1 0
C 1 0 0 1 1 0
D 1 1 1 0 1 1
E 0 1 0 1 0 1
F 0 0 1 1 1 0
Output:
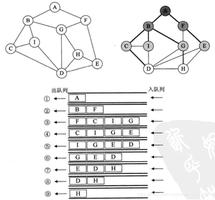
DFS Traversal: C F E B D A
算法
dfs(vertices, start)
输入:所有顶点的列表以及起始节点。
输出: 遍历图中的所有节点。
Begininitially make the state to unvisited for all nodes
push start into the stack
while stack is not empty, do
pop element from stack and set to u
display the node u
if u is not visited, then
mark u as visited
for all nodes i connected to u, do
if ith vertex is unvisited, then
push ith vertex into the stack
mark ith vertex as visited
done
done
End
示例
#include<iostream>#include<stack>
using namespace std;
#define NODE 6
typedef struct node {
int val;
int state; //status
}node;
int graph[NODE][NODE] = {
{0, 1, 1, 1, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 1, 0, 1},
{1, 1, 1, 0, 1, 1},
{0, 1, 0, 1, 0, 1},
{0, 0, 1, 1, 1, 0}
};
void dfs(node *vertex, node start) {
node u;
stack<node> myStack;
for(int i = 0; i<NODE; i++) {
vertex[i].state = 0; //not visited
}
myStack.push(start);
while(!myStack.empty()) {
//弹出并打印节点
u = myStack.top();
myStack.pop();
cout << char(u.val+'A') << " ";
if(u.state != 1) {
//将顶点状态更新为已访问
u.state = 1;
vertex[u.val].state = 1;
for(int i = 0; i<NODE; i++) {
if(graph[i][u.val]) {
if(vertex[i].state == 0) {
myStack.push(vertex[i]);
vertex[i].state = 1;
}
}
}
}
}
}
int main() {
node vertices[NODE];
node start;
char s;
for(int i = 0; i<NODE; i++) {
vertices[i].val = i;
}
s = 'C'; //starting vertex C
start.val = s-'A';
cout << "DFS Traversal: ";
dfs(vertices, start);
cout << endl;
}
输出结果
DFS Traversal: C F E B D A
以上是 图的深度优先搜索(DFS) 的全部内容, 来源链接: utcz.com/z/343229.html