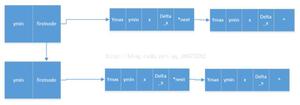
区分非确定性、确定性和图灵机计算模型?
让我们首先了解计算理论 (TOC) 中确定性有限自动机 (DFA) 的概念。
确定性有限自动机 (DFA)
在 DFA 中,对于每个信息图像,可以决定机器将移动到的状态。此后,它被称为确定性自动机。
形式定义- 确定性有限自动机是一个 5 元组
M=(Q, ∑, δ,q0,F)
在哪里,
Q - 称为状态的有限集。
∑ - 称为字母表的有限集。
δ − Q × ∑ → Q 是转移函数。
q0 ∈ − Q 是开始或初始状态。
F - 最终或接受状态。
非确定性有限自动机 (NDFA)
在 NDFA 中,对于特定的信息图像,机器可以移动到机器中的任何状态组合。总而言之,无法解析机器移动到的具体状态。此后,它被称为非确定性自动机。
正式定义-NDFA 也有五个与 DFA 相同的状态,但具有不同的转换函数,如下所示 -
δ:QX ∑ -> 2 Q
在哪里,
Q - 有限状态集。
∑ - 输入符号的有限集。
q0 - 初始状态。
F - 最终状态。
δ - 过渡函数。
非确定性下推自动机 (NPDA)
非确定性下推自动机很像 NDFA。我们将讨论一些承认 NPDA 的上下文无关文法 (CFG)。
确认确定性 PDA (DPDA) 的 CFG 也确认非确定性 PDA。本质上,有一些 CFG 可以简单地由 NPDA 确认,而不是由 DPDA 确认。
从这个角度来看,NPDA 比 DPDA 更令人印象深刻。
图灵机
图灵机 (TM) 是一种数值模型,它包含一个无限长的带子,该带子被划分为给出信息的单元格。
正式定义
图灵机是一个 7 元组 (Q, ∑, Γ, δ, q0, qaccept , qreject)
在哪里,
Q 是有限状态集。
∑ 是不包含空白符号 t 的输入字母表。
Γ 是磁带字母表,其中 t ∈ Γ 和 ∑ ⊆ Γ。
δ:(Q × Γ) → (Q × Γ × {L, R}) 是转移函数。
q0 ∈ Q 是起始状态。
qaccept ∈ Q 是接受状态。
qreject ∈ Q 是拒绝状态,其中 qreject ≠ qaccept。
差异
尽管在 NDFA 许可中,无效字符串更改在 DFA 中没有看到。
DFA 和 NDFA 中允许回溯,但通常无法想象回溯。
NPDA 比有限状态机更强大,但不如车削机。
以上是 区分非确定性、确定性和图灵机计算模型? 的全部内容, 来源链接: utcz.com/z/341385.html