霍夫曼编码
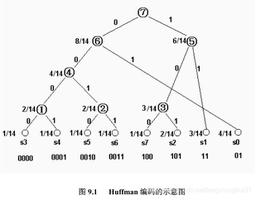
编码" title="霍夫曼编码">霍夫曼编码是无损数据压缩算法。在此算法中,分配了可变长度代码以输入不同的字符。代码长度与字符使用频率有关。最频繁的字符具有最小的代码,而较长的代码则用于最不频繁的字符。
主要有两个部分。第一个创建霍夫曼树,另一个遍历该树以查找代码。
例如,考虑一些字符串“ YYYZXXYYX”,字符Y的频率大于X,字符Z的频率最小。因此,Y的代码长度小于X,X的代码长度将小于Z。
根据每个字符的频率分配代码的复杂度为O(n log n)
输入 -不同字符的字符串,例如“ ACCEBFFFFAAXXBLKE”。
输出 -不同字符的代码:
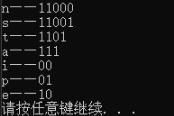
Data: K, Frequency: 1, Code: 0000Data: L, Frequency: 1, Code: 0001
Data: E, Frequency: 2, Code: 001
Data: F, Frequency: 4, Code: 01
Data: B, Frequency: 2, Code: 100
Data: C, Frequency: 2, Code: 101
Data: X, Frequency: 2, Code: 110
Data: A, Frequency: 3, Code: 111
算法
huffmanCoding(字符串)
输入-不同字符的字符串。
输出-每个字符的代码。
Begindefine a node with character, frequency, left and right child of the node for Huffman tree.
create a list ‘freq’ to store frequency of each character, initially all are 0
for each character c in the string do
increase the frequency for character ch in freq list.
done
for all type of character ch do
if the frequency of ch is non zero then add ch and its frequency as a node of priority queue Q.
done
while Q is not empty do
remove item from Q and assign it to left child of node
remove item from Q and assign to the right child of node
traverse the node to find the assigned code
done
End
traverseNode(n:节点,代码)
输入-霍夫曼树的节点n,以及上一次调用分配的代码
输出-每个字符分配的代码
if left child of node n ≠ φ thentraverseNode(leftChild(n), code+’0’) //traverse through the left child
traverseNode(rightChild(n), code+’1’) //traverse through the right child
else
display the character and data of current node.
示例
#include<iostream>#include<queue>
#include<string>
using namespace std;
struct node{
int freq;
char data;
const node *child0, *child1;
node(char d, int f = -1){ //assign values in the node
data = d;
freq = f;
child0 = NULL;
child1 = NULL;
}
node(const node *c0, const node *c1){
data = 0;
freq = c0->freq + c1->freq;
child0=c0;
child1=c1;
}
bool operator<( const node &a ) const { //< operator performs to find priority in queue
return freq >a.freq;
}
void traverse(string code = "")const{
if(child0!=NULL){
child0->traverse(code+'0'); //add 0 with the code as left child
child1->traverse(code+'1'); //add 1 with the code as right child
}else{
cout << "Data: " << data<< ", Frequency: "<<freq << ", Code: " << code<<endl;
}
}
};
void huffmanCoding(string str){
priority_queue<node> qu;
int frequency[256];
for(int i = 0; i<256; i++)
frequency[i] = 0; //clear all frequency
for(int i = 0; i<str.size(); i++){
frequency[int(str[i])]++; //increase frequency
}
for(int i = 0; i<256; i++){
if(frequency[i]){
qu.push(node(i, frequency[i]));
}
}
while(qu.size() >1){
node *c0 = new node(qu.top()); //get left child and remove from queue
qu.pop();
node *c1 = new node(qu.top()); //get right child and remove from queue
qu.pop();
qu.push(node(c0, c1)); //add freq of two child and add again in the queue
}
cout << "The Huffman Code: "<<endl;
qu.top().traverse(); //traverse the tree to get code
}
main(){
string str = "ACCEBFFFFAAXXBLKE"; //arbitray string to get frequency
huffmanCoding(str);
}
输出结果
The Huffman Code:Data: K, Frequency: 1, Code: 0000
Data: L, Frequency: 1, Code: 0001
Data: E, Frequency: 2, Code: 001
Data: F, Frequency: 4, Code: 01
Data: B, Frequency: 2, Code: 100
Data: C, Frequency: 2, Code: 101
Data: X, Frequency: 2, Code: 110
Data: A, Frequency: 3, Code: 111
以上是 霍夫曼编码 的全部内容, 来源链接: utcz.com/z/340803.html