python验证多组数据之间有无显著差异
一、方差分析
1.单因素方差分析

通过箱线图可以人肉看出10组的订单量看起来差不多,为了更科学比较10组的订单量有无显著差异,我们可以利用方差分析
from statsmodels.formula.api import olsfrom statsmodels.stats.anova import anova_lm
model = ols('orders~C(label)',data=need_data).fit()
anova_table = anova_lm(model, typ = 2)
print(anova_table)

结果显示,p值为0.62大于0.05,不能拒绝原假设,所以这10组的订单量分布没有显著差异。
二、卡方检验
如果是比较多组之间的非连续值指标是否存在差异呢?
如检查上面10组的男女比例是否存在显著差异
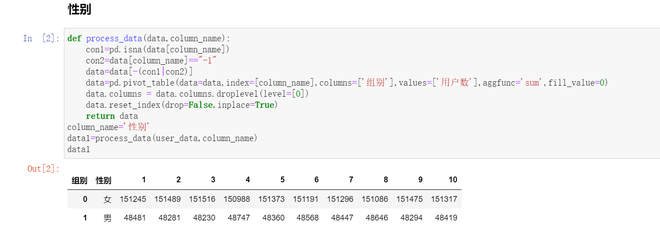
计算各组观察频数:
data2=data1.melt(id_vars=['性别'],value_name='观察频数')data2.head()

计算总体的男女比例:
rate=(data2.groupby(['性别'])['观察频数'].sum()/data2.groupby(['性别'])['观察频数'].sum().sum()).reset_index()rate.columns=['性别','rate']
rate
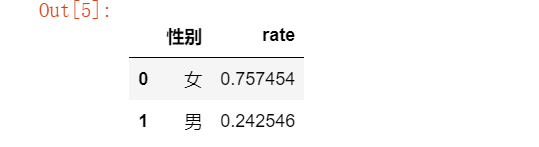
计算各组用户总数:
group_sum=data2.groupby(['组别'])['观察频数'].sum().reset_index()group_sum.columns=['组别','组内用户数']
group_sum
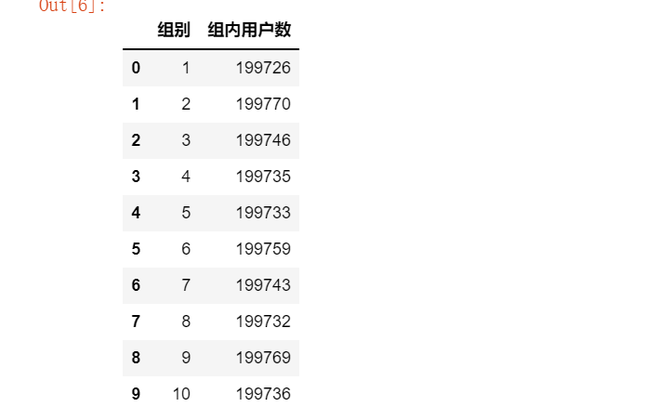
计算卡方值:
import mathdata3=pd.merge(data2,group_sum,on=['组别'],how='left')
data3=pd.merge(data3,rate,on=['性别'],how='left')
data3['期望频数']=data3['组内用户数']*data3['rate']
data3['卡方值']=data3.apply(lambda x: math.pow((x.期望频数-x.观察频数),2)/x.期望频数,axis=1)
data3.head()
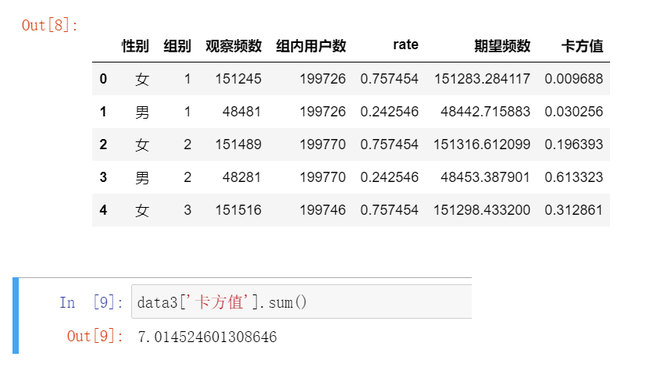
本案例的自由度为(10-1)*(2-1)=9,选取显著性水平为0.05,查卡方分布表得临界值为18.31因为7.01<18.31,所以不能拒绝原假设,即各组的性别分布不存在显著性差异。
到此这篇关于python验证多组数据之间有无显著差异的文章就介绍到这了,更多相关python验证多组数据之间有无显著差异内容请搜索以前的文章或继续浏览下面的相关文章希望大家以后多多支持!
以上是 python验证多组数据之间有无显著差异 的全部内容, 来源链接: utcz.com/z/257008.html