python二分法查找函数底值

  • Z时代
  • 2024-01-10
  • 分类：综合

假设连续函数f(x)在区间(a,b)上有一个底值m，且在该底值下的函数输出值为M，即f(m)=M，利用二分法查找该底值：(s为足够小的数）

令t=(a+b)/2，若|f(t)-M|<=s，则m=t，若|f(t)-M|>s，如果(f(t)-M)和(f(a)-M)同号，a=t，反之b=t，继续二分法t=(a+b)/2...直到|f(t)-M|<=s，则m=t。

例如：一项一年期投资，每个季度初投入10000元，期满时收入44163.225，求内部收益率(已设定为0.04)。

收益函数为：

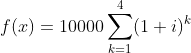
f(x)=10000\sum_{k=1}^{4}(1+i)^{k}

从(0,1)区间中查找该内部收益率，用二分法令t=(0+1)/2=0.5，比较发现|f(t)-44163.225|>10**(-10)，并且f(t)-44163.225和f(1)-44163.225同号，则继续令t=(0+0.5)/2=0.25，，，直到查找出内部收益率为0.03999999445689362，约等于0.04

def f(i):
    y = 10000 * (1 + i) ** 4 + 10000 * (1 + i) ** 3 + 10000*(1+i)**2+10000*(1+i)**1
    return y
def division(a,b,M,n):
    #a,b为自选值范围，(f(a)-M)*(F(b)-M)<或=0
    #M为f(x)输出值，n为输出值精度要求小数位数
    while True:
        t = (a + b) / 2
        if abs(f(t) - M) <= 10 ** (-n):
            m = t
            break
        if (f(t) - M) / abs(f(t) - M) == (f(a) - M) / abs(f(a) - M):
            a = t
        else:
            b = t
    return m
y=division(0,1,44163.225,10)
print(y)

到此这篇关于python二分法查找函数底值的文章就介绍到这了,更多相关python函数底值内容请搜索以前的文章或继续浏览下面的相关文章希望大家以后多多支持！

以上是 python二分法查找函数底值 的全部内容， 来源链接： utcz.com/z/256980.html

回到顶部