关于时间区间分割算法问题
背景:
对 非连续的多个有序的时间区间进行 分割,结果是拆分出更小的时间区间,基本规则就是 对于时间区间 A来说,如果有 时间区间B 与A有交集,则 用B对A进行分割,举例如下:
1-9:表示 1号到9号
时间区间A: 1-9、10-29、30-31
例子1:
时间区间B: 1-8、9-19、20-31
那么用B对A进行分割,结果应该是:
1-8、9-9、10-19、20-29、30-31
例子2:
时间区间B: 4-8、9-19、20-28
那么用B对A进行分割,结果应该是:
1-3、4-8、9-9、10-19、20-28、29-29、30-31
1-9、10-29、30-31
例子3:
时间区间B: 8-8、9-19、20-31
那么用B对A进行分割,结果应该是:
1-7、8-8、9-9、10-19、20-29、30-31
求助该如何进行切割?
回答:
方便其他看,加一段说明[1,9],[10,19],[20,31] 这个时间段,我们理解为一个月休3次。分别是[9,10],[19,20],[31,1],也就是0.5,9.5和19.5
也就是说有个隐藏的[32,0]
而这三个点,我们实际上可以用0,9,19来表示,需要右端的时候,再+1即可。
我们用二进制按位取的思路来记录这个时间点就是 1 000 000 000 100 000 001
从右向左看第0,9,19位分别是 1,表示休息日。函数getLeft就做了如上处理,把带端点的数组转化为二进制数。
试了一下,早上的回答有问题,join不能这么用,重新写一个
实际上我们只需要定位分割点就可以了
那观察问题,不难看出是要对月内的日期分割,那么自然是个整数日期,而且一个月最多只有31天,与整数最大31位不谋而合。于是嘛。。。
function getLeft(params: number[][]) { return params.reduce((pre, cur) => {
let left = 1 << cur[0] - 1
let right = 1 << cur[1] % 31 // 超出31日的相当于次月
return pre | left | right
}, 0)
}
function parting(a: number[][], b:number[][]) {
let lefts = getLeft(a) | getLeft(b)
let index = 31
let result:number[][] = [[31]]
while (index>=0) {
let bParting = lefts & 1 << index
if (bParting ) { // bParting != 0 表示被占位
result[result.length-1].push(index+1)
if(index>0)
result.push([index])
}
index--;
}
return result
}
测试一下
let a = [[1,9], [10, 29], [30, 31]]
parting(a, [[1, 8], [9, 19], [20, 31]])
// [ [ 31, 30 ], [ 29, 20 ], [ 19, 10 ], [ 9, 9 ], [ 8, 1 ] ]
parting(a, [[4, 8], [9, 19], [20, 28]])
// [[31, 30], [29, 29], [28, 20], [19, 10], [9, 9], [8, 4], [3, 1] ]
parting(a, [[8, 8], [9, 19], [20, 31]])
// [ [ 31, 30 ], [ 29, 20 ], [ 19, 10 ], [ 9, 9 ], [ 8, 8 ], [ 7, 1 ] ]
旧答案
如果是整数分隔的话,我有个想法,可以试一试
function active(a: number[][], b: number[][]) { let c = a.join(0)
let d = b.join(0)
while (d[0] != 1) {
d = [d[0] - 1, …d]
}
let f: number[] = []
let index = 0
while (c[index] || d[index]) {
let q = c[index]
let w = d[index]
if (q) f.join(q)
if (w) f.join(w)
}
}
return f.spilt(0) // 分隔前做一步去重就可以了
试试
let a = [[1,2,3…9],[10,11…28,29],[30,31]]let b = [[1,2,3…8],[9,11…18,19],[20,21…31]]
c.log ( active(a, b) )
回答:
虽然描述的是用小区间切割大区间,实际则为数字组,对一整个月的重排切分。
思路是首先将数字组按开始时间升序排,取两条比较,按情况分类讨论。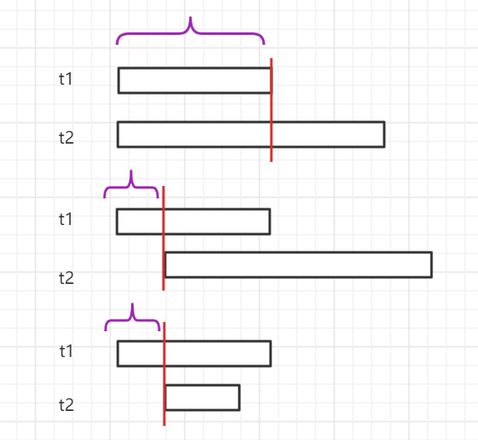
(1)两端对齐,取短的一端作为结束;
(2)开端t2>t1,则截取的区间为[t1.start,t2.start)
更新两条线段的起始值,如果其中一条线段被消耗完了,则取一条新的线段。
由于原始两条线段被处理过,新取的线段起始时间可能会更小,所以采用swap,始终保持t1的起始时间更小,同时可以减少上述讨论的情况(毕竟是对称的)。
最后注意处理循环结束的边界情况,把剩余的一条放入结果集合。
思路大概就是这样,代码写的比较口水化,看看就行
public static List<Date> timeRangeSplit(List<Tuple2<Date, Date>> baseSeg, List<Tuple2<Date, Date>> seg1) { List<Date> res = new ArrayList<>();
// 所有数据按起始时间排序
baseSeg.addAll(seg1);
baseSeg = baseSeg.stream().sorted().collect(Collectors.toList());
Tuple2<Date, Date> t1 = baseSeg.get(0);
Tuple2<Date, Date> t2 = baseSeg.get(1);
Integer curIdx = 2;
while (null != t1 && null != t2) {
// 保证t1的起始时间更小
Date end;
if (t1._1.compareTo(t2._1) == 0) {
if (t1._2.compareTo(t2._2) <= 0) {
// t1短
end = t1._2;
} else {
end = t2._2;
}
} else {
// t2的起点把t1截成两段
end = DateDealUtils.minusByDay(t2._1, 1);
}
res.add(t1._1);
res.add(end);
t1 = t1.update1(DateDealUtils.plusByDay(end, 1));
t2 = t2.update1(DateDealUtils.plusByDay(end, 1));
if (t1._1.compareTo(t1._2) > 0) {
if (curIdx < baseSeg.size()) {
t1 = baseSeg.get(curIdx++);
} else {
t1 = null;
break;
}
}
if (t2._1.compareTo(t2._2) > 0) {
if (curIdx < baseSeg.size()) {
t2 = baseSeg.get(curIdx++);
} else {
t2 = null;
break;
}
}
if (t1._1.compareTo(t2._1) > 0) {
// swap 始终保持t1开始数字小
Tuple2<Date, Date> tmp = Tuple.of(t1._1, t1._2);
t1 = Tuple.of(t2._1, t2._2);
t2 = Tuple.of(tmp._1, tmp._2);
}
}
// 循环终止后,把剩余部分放入结果
if (null != t1 && t1._1.compareTo(t1._2) < 0) {
res.add(t1._1);
res.add(t1._2);
}
if (null != t2 && t2._1.compareTo(t2._2) < 0) {
res.add(t2._1);
res.add(t2._2);
}
return res;
}
回答:
你的 \( A \) 区间序列是这样的

前后区间是紧贴在一起的,如果是这种的话,可以用连接处端点序列来表示:
$$
1-9、10-29、30-31 \Rightarrow 1、10、30、32
$$
然后就可以用合并两个有序数组的算法,合并 \( AB \),取 \( A \) 首端点到 \( A \) 末端点就得到结果
参考代码(js):
const minusAndIntersect = (A, B) => { const R = []
if (A.length == 0) return R
let iB = 0
while (iB < B.length && B[iB] <= A[0]) ++iB
R.push(A[0])
for (let iA = 1; iA < A.length; ++iA) {
while (iB < B.length && B[iB] <= A[iA]) R.push(B[iB++])
if (A[iA] > R.at(-1)) R.push(A[iA])
}
return R
}
const A = [1, 10, 30, 32]
console.log(minusAndIntersect(A, [1, 9, 20, 32])) // [1, 9, 10, 20, 30, 32]
console.log(minusAndIntersect(A, [4, 9, 20, 29])) // [1, 4, 9, 10, 20, 29, 30, 32]
console.log(minusAndIntersect(A, [8, 9, 20, 32])) // [1, 8, 9, 10, 20, 30, 32]
如果前后区间不是紧贴的,如 \( 1-10、21-30 \)

那么用 \( B \) 的端点对 \( A \) 进行分割即可
参考代码(js):
const minusAndIntersect = (A, B) => { const R = []
if (A.length == 0) return R
B = B.flat()
for (let i = 1; i < B.length; i += 2) ++B[i]
let iB = 0
for (const a of A) {
let [begin, end] = a
while (iB < B.length && B[iB] <= begin) ++iB
while (iB < B.length && B[iB] <= end) {
if (B[iB] > begin) {
R.push([begin, B[iB] - 1])
begin = B[iB]
}
++iB
}
R.push([begin, end])
}
return R
}
const A = [[1, 9], [10, 29], [30, 31]]
console.log(minusAndIntersect(A, [[1, 8], [9, 19], [20, 31]])) // [[1,8],[9,9],[10,19],[20,29],[30,31]]
console.log(minusAndIntersect(A, [[4, 8], [9, 19], [20, 28]])) // [[1,3],[4,8],[9,9],[10,19],[20,28],[29,29],[30,31]]
console.log(minusAndIntersect(A, [[8, 8], [9, 19], [20, 31]])) // [[1,7],[8,8],[9,9],[10,19],[20,29],[30,31]]
// 前后区间不紧贴的例子
console.log(minusAndIntersect([[1, 10], [21, 30]], [[6, 25]])) // [[1,5],[6,10],[21,25],[26,30]]
参考代码(java):
public static void main(String[] args) { MinusAndIntersect f = new MinusAndIntersect(ranges(1, 9, 10, 29, 30, 31));
System.out.println(f.exec(ranges(1, 8, 9, 19, 20, 31)));
System.out.println(f.exec(ranges(4, 8, 9, 19, 20, 28)));
System.out.println(f.exec(ranges(8, 8, 9, 19, 20, 31)));
// 前后区间不紧贴的例子
System.out.println(new MinusAndIntersect(ranges(1, 10, 21, 30)).exec(ranges(6, 25)));
/*
[1-8, 9-9, 10-19, 20-29, 30-31]
[1-3, 4-8, 9-9, 10-19, 20-28, 29-29, 30-31]
[1-7, 8-8, 9-9, 10-19, 20-29, 30-31]
[1-5, 6-10, 21-25, 26-30]
*/
}
static List<Range> ranges(int... beginAndEnd) {
int n = beginAndEnd.length;
List<Range> ranges = new ArrayList<>(n >>> 1);
for (int i = 0; i < n; ranges.add(new Range(beginAndEnd[i++], beginAndEnd[i++])));
return ranges;
}
static class Range {
int begin, end;
Range(int beginInclusive, int endInclusive) {
begin = beginInclusive;
end = endInclusive;
}
@Override
public String toString() {
return begin + "-" + end;
}
}
static class MinusAndIntersect {
Range[] A;
List<Range> R;
int i = -1, begin, end;
MinusAndIntersect(List<Range> A) {
this.A = A.toArray(new Range[A.size()]);
}
List<Range> exec(List<Range> B) {
R = new ArrayList<>();
if (next()) {
for (Range b : B)
if (!addUntil(b.begin - 1) || !addUntil(b.end)) return R;
addUntil(Integer.MAX_VALUE);
}
return R;
}
boolean addUntil(int last) {
while (begin <= last) {
if (end <= last) {
R.add(new Range(begin, end));
if (!next()) return false;
} else {
R.add(new Range(begin, last));
begin = last + 1;
break;
}
}
return true;
}
boolean next() {
if (++i == A.length) {
i = -1;
return false;
}
Range a = A[i];
begin = a.begin;
end = a.end;
return true;
}
}
回答:
两个时间段列表是有序的,均取最小的一个时间段来处理,他们可能有如下几种关系(以及处理)
完全分离,
把小的那个取出来,大的那个留着下一轮比较用
存在交叉
按交叉点切割成 3 部分,取前 2 部分,最后一部分留着下一轮比较用
重合
完全重合
任取一个,两个都不留
前端重合
最小的一个,大的那个切割后留着下一轮比较用
后端重合
切割成两段,都取走不留
包含
切割成三段,取走前两段,留下最后一段
如果这个分析没问题,就是一种一种情况去处理,目前还没发现简洁算法。昨天想了一个,但是代码验证是错的。先看看大家有没有简单点的算法,再来考虑代码怎么实现。
以上是 关于时间区间分割算法问题 的全部内容, 来源链接: utcz.com/p/944556.html