深入解析快速排序算法的原理及其Go语言版实现

  • Z时代
  • 2024-01-10
  • 分类：IT

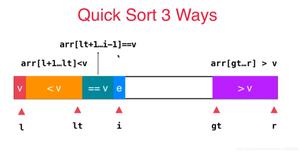
快速排序是一种基于分治技术的重要排序算法。不像归并排序是按照元素在数组中的位置对它们进行划分，快速排序按照元素的值对它们进行划分。具体来说，它对给定数组中的元素进行重新排列，以得到一个快速排序的分区。在一个分区中，所有在s下标之前的元素都小于等于A[s]，所有在s下标之后的元素都大于等于A[s]。

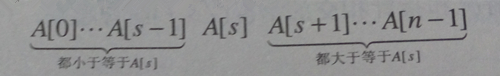
2016413103715116.jpg (500×76)

显然，建立了一个分区以后，A[s]已经位于它在有序数组中的最终位置，接下来我们可以继续对A[s]前和A[s]后的子数组分别进行排序（使用同样的方法）。

为了排序一个数组A的全部元素，初始调用的是QUICKSORT(A,1，A.length)。

下面的算法对A[p..r]进行分区（先伪代码一下、领会意思）。

PARTITION(A,p,r)
 x = A[r]
 i = p - 1
 for j = p to r - 1
  if A[j] ≤ x
   i = i + 1
   exchange A[i] with A[j]
 exchange A[i+1] with A[r]
 return i+1

快速排序算法的效率：

在最优情况下，键值比较的次数Cbest(n)满足下面的递推式：

当n>1时，Cbest(n)=2Cbest(n/2)+n，Cbest(1)=0

根据主定理，Cbest(n)∈Θ(nlogn)；对于n=2k的情况求得Cbest(n) = nlog(n)。

在最差的情况下，所有的分裂点都趋于极端：两个子数组有一个为空，而另一个子数组仅仅比被分区的数组少一个元素。具体来说，这种令人遗憾的情况会发生在升序的数组上，也就是说输入的数组已经被排过序了。所以，在进行了n+1次比较之后建立了分区，并且将A[0]和它本身进行了交换以后，快速排序算法还会对严格递增的数组A[1..n-1]进行排序。对规模减小了的严格递增数组的排序会一直继续到最后一个子数组A[n-2..n-1]。这种情况下，键值比较的总次数应该等于：

Cworst(n)=(n+1)+n+...+3=(n+1)(n+2)/2-3∈Θ(n2)

现在，轮到讨论快速排序在平均情况下的效率了。对于大小为n的随机排列的数组，快速排序的平均键值比较次数记为Cavg(n)。假设分区的分裂点s（0≤s≤n-1)位于每个位置的概率都是1/n，我们得到下面的递推关系式：

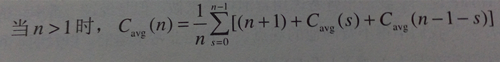
2016413103740781.jpg (500×62)

Cavg(0)=0，Cavg(1)=0

Cavg(n)≈2nlnn≈1.38nlogn

因此，快速排序在平均情况下，仅比最优情况多执行38%的比较操作。此外，它的最内层循环效率非常高，使得在处理随机排列的数组时，速度要比归并排序快。

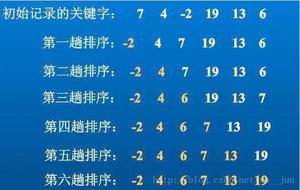
以下是快速排序的Go代码：

复制代码 代码如下:

func QuickSort(slice_arg []int, iLeft int, iRight int) {

    if iLeft < iRight {

        var iTmpVal = slice_arg[iLeft]

        var i, j = iLeft, iRight

        for i < j {

            fmt.Println("i,j = ", i, j)

            for i < j && slice_arg[j] > iTmpVal {

                j--

            }

            if i < j {

                slice_arg[i] = slice_arg[j]

                i++

            }

            for i < j && slice_arg[i] < iTmpVal {

                i++

            }

            if i < j {

                slice_arg[j] = slice_arg[i]

                j--

            }

        }

        slice_arg[i] = iTmpVal

        QuickSort(slice_arg, iLeft, i-1)

        QuickSort(slice_arg, j+1, iRight)

    }

}

以上是 深入解析快速排序算法的原理及其Go语言版实现 的全部内容， 来源链接： utcz.com/p/234958.html

回到顶部