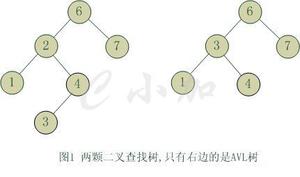
PHP实现绘制二叉树图形显示功能详解【包括二叉搜索树、平衡树及红黑树】
本文实例讲述了PHP实现绘制二叉树图形显示功能。分享给大家供大家参考,具体如下:
前言:
最近老师布置了一个作业:理解并实现平衡二叉树和红黑树,本来老师是说用C#写的,但是我学的C#基本都还给老师了,怎么办?那就用现在最熟悉的语言PHP来写吧!
有一个问题来了,书上在讲解树的时候基本上会给出形象的树形图。但是当我们自己试着实现某种树,在调试、输出的时候确只能以字符的形式顺序地输出。这给调试等方面带来了很大的不便。然后在各种百度之后,我发现利用PHP实现二叉树的图形显示的资源几乎是零!好吧,那我就自己个儿实现一个!
效果显示:
如果我是直接在这一步摆代码的话,估计大家会比较烦闷,那我就直接上结果吧,后面在补代码,先激发激发大家的阅读兴趣:
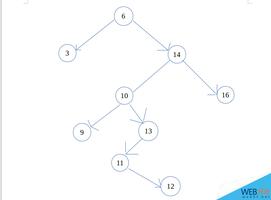
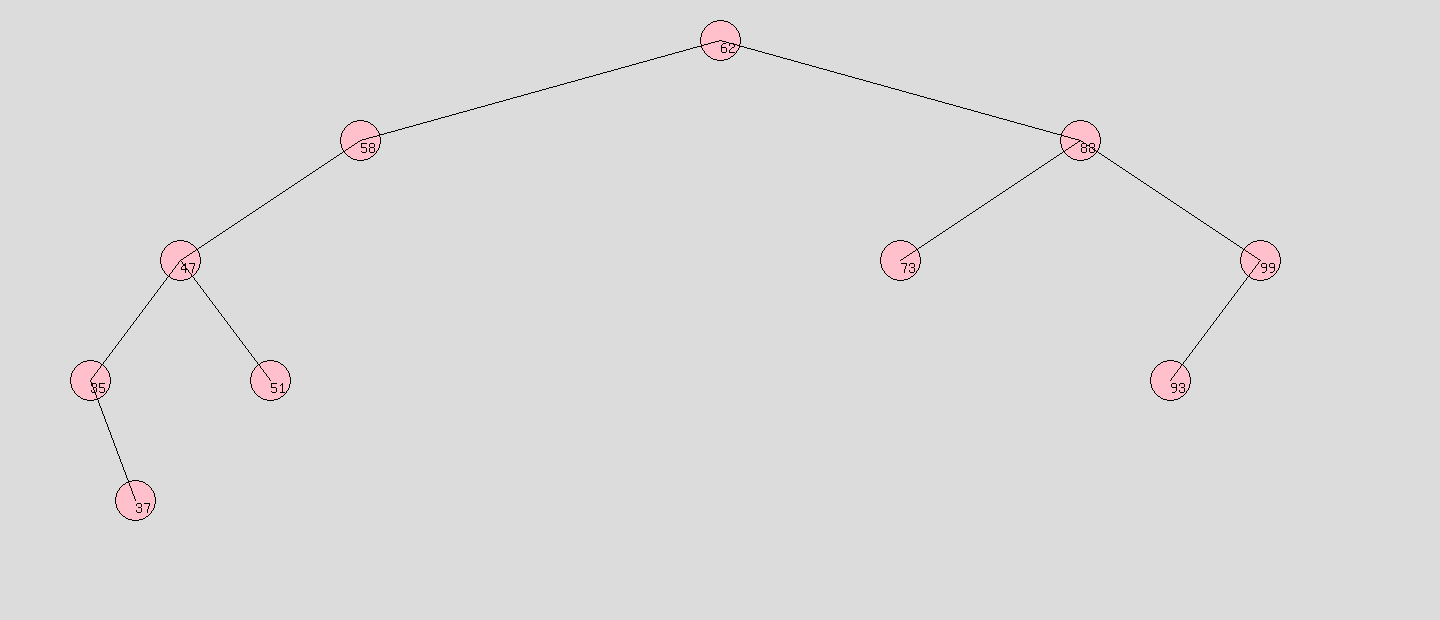
1、搜索二叉树:
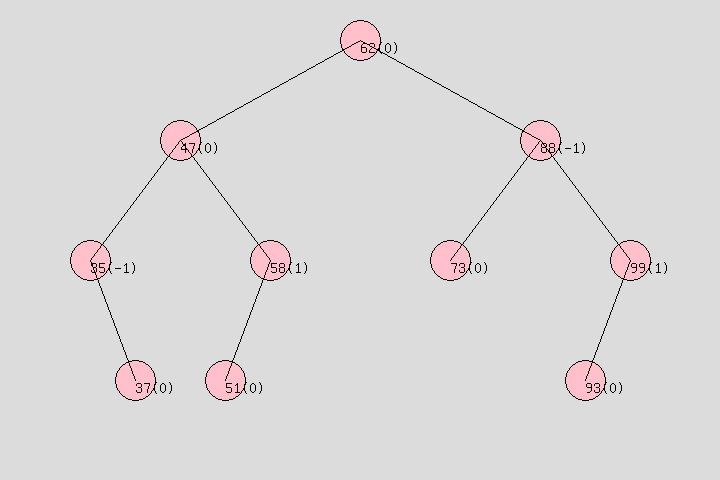
2、平衡二叉树:
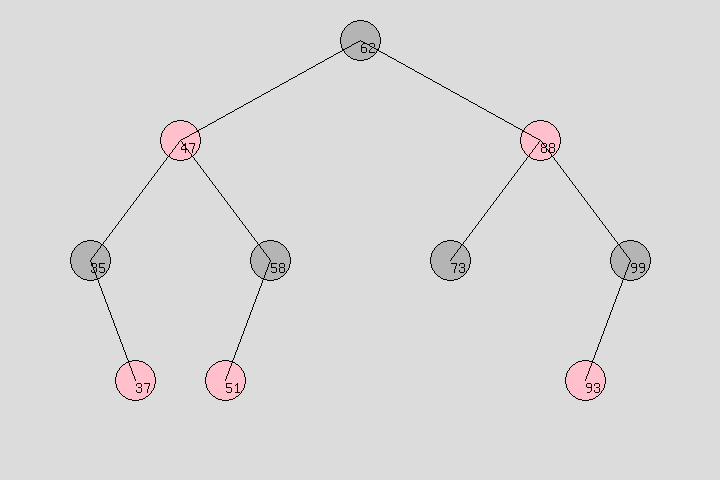
3、红黑树:
上代码:
我们给图片创建一个类吧,显得稍微的小高级:
image.php 文件:
<?php
/**
* author:LSGOZJ
* description: 绘制二叉树图像
*/
class image
{
//树相关设置
//每层之间的间隔高度
private $level_high = 100;
//最底层叶子结点之间的宽度
private $leaf_width = 50;
//结点圆的半径
private $rad = 20;
//根节点离边框顶端距离
private $leave = 20;
//树(保存树对象的引用)
private $tree;
//树的层数
private $level;
//完全二叉树中最底层叶子结点数量(计算图像宽度时用到,论如何实现图片大小自适应)
private $maxCount;
//图像相关设置
//画布宽度
private $width;
//画布高度
private $height;
//画布背景颜色(RGB)
private $bg = array(
220, 220, 220
);
//节点颜色(搜索二叉树和平衡二叉树时用)
private $nodeColor = array(
255, 192, 203
);
//图像句柄
private $image;
/**
* 构造函数,类属性初始化
* @param $tree 传递一个树的对象
* @return null
*/
public function __construct($tree)
{
$this->tree = $tree;
$this->level = $this->getLevel();
$this->maxCount = $this->GetMaxCount($this->level);
$this->width = ($this->rad * 2 * $this->maxCount) + $this->maxCount * $this->leaf_width;
$this->height = $this->level * ($this->rad * 2) + $this->level_high * ($this->level - 1) + $this->leave;
//1.创建画布
$this->image = imagecreatetruecolor($this->width, $this->height); //新建一个真彩色图像,默认背景是黑色
//填充背景色
$bgcolor = imagecolorallocate($this->image, $this->bg[0], $this->bg[1], $this->bg[2]);
imagefill($this->image, 0, 0, $bgcolor);
}
/**
* 返回传进来的树对象对应的完全二叉树中最底层叶子结点数量
* @param $level 树的层数
* @return 结点数量
*/
function GetMaxCount($level)
{
return pow(2, $level - 1);
}
/**
* 获取树对象的层数
* @param null
* @return 树的层数
*/
function getLevel()
{
return $this->tree->Depth();
}
/**
* 显示二叉树图像
* @param null
* @return null
*/
public function show()
{
$this->draw($this->tree->root, 1, 0, 0);
header("Content-type:image/png");
imagepng($this->image);
imagedestroy($this->image);
}
/**
* (递归)画出二叉树的树状结构
* @param $root,根节点(树或子树) $i,该根节点所处的层 $p_x,父节点的x坐标 $p_y,父节点的y坐标
* @return null
*/
private function draw($root, $i, $p_x, $p_y)
{
if ($i <= $this->level) {
//当前节点的y坐标
$root_y = $i * $this->rad + ($i - 1) * $this->level_high;
//当前节点的x坐标
if (!is_null($parent = $root->parent)) {
if ($root == $parent->left) {
$root_x = $p_x - $this->width / (pow(2, $i));
} else {
$root_x = $p_x + $this->width / (pow(2, $i));
}
} else {
//根节点
$root_x = (1 / 2) * $this->width;
$root_y += $this->leave;
}
//画结点(确定所画节点的类型(平衡、红黑、排序)和方法)
$method = 'draw' . get_class($this->tree) . 'Node';
$this->$method($root_x, $root_y, $root);
//将当前节点和父节点连线(黑色线)
$black = imagecolorallocate($this->image, 0, 0, 0);
if (!is_null($parent = $root->parent)) {
imageline($this->image, $p_x, $p_y, $root_x, $root_y, $black);
}
//画左子节点
if (!is_null($root->left)) {
$this->draw($root->left, $i + 1, $root_x, $root_y);
}
//画右子节点
if (!is_null($root->right)) {
$this->draw($root->right, $i + 1, $root_x, $root_y);
}
}
}
/**
* 画搜索二叉树结点
* @param $x,当前节点的x坐标 $y,当前节点的y坐标 $node,当前节点的引用
* @return null
*/
private function drawBstNode($x, $y, $node)
{
//节点圆的线颜色
$black = imagecolorallocate($this->image, 0, 0, 0);
$nodeColor = imagecolorallocate($this->image, $this->nodeColor[0], $this->nodeColor[1], $this->nodeColor[2]);
//画节点圆
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
//节点圆颜色填充
imagefill($this->image, $x, $y, $nodeColor);
//节点对应的数字
imagestring($this->image, 4, $x, $y, $node->key, $black);
}
/**
* 画平衡二叉树结点
* @param $x,当前节点的x坐标 $y,当前节点的y坐标 $node,当前节点的引用
* @return null
*/
private function drawAvlNode($x, $y, $node)
{
$black = imagecolorallocate($this->image, 0, 0, 0);
$nodeColor = imagecolorallocate($this->image, $this->nodeColor[0], $this->nodeColor[1], $this->nodeColor[2]);
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
imagefill($this->image, $x, $y, $nodeColor);
imagestring($this->image, 4, $x, $y, $node->key . '(' . $node->bf . ')', $black);
}
/**
* 画红黑树结点
* @param $x,当前节点的x坐标 $y,当前节点的y坐标 $node,当前节点的引用
* @return null
*/
private function drawRbtNode($x, $y, $node)
{
$black = imagecolorallocate($this->image, 0, 0, 0);
$gray = imagecolorallocate($this->image, 180, 180, 180);
$pink = imagecolorallocate($this->image, 255, 192, 203);
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
if ($node->IsRed == TRUE) {
imagefill($this->image, $x, $y, $pink);
} else {
imagefill($this->image, $x, $y, $gray);
}
imagestring($this->image, 4, $x, $y, $node->key, $black);
}
}
好,现在我们来看看在客户端如何调用:
client.php
class Client
{
public static function Main()
{
try {
//实现文件的自动加载
function autoload($class)
{
include strtolower($class) . '.php';
}
spl_autoload_register('autoload');
$arr = array(62, 88, 58, 47, 35, 73, 51, 99, 37, 93);
// $tree = new Bst(); //搜索二叉树
$tree = new Avl(); //平衡二叉树
// $tree = new Rbt(); //红黑树
$tree->init($arr); //树的初始化
// $tree->Delete(62);
// $tree->Insert(100);
// $tree->MidOrder(); //树的中序遍历(这也是调试的一个手段,看看数字是否从小到大排序)
$image = new image($tree);
$image->show(); //显示图像
} catch (Exception $e) {
echo $e->getMessage();
}
}
}
Client::Main();
这里用到的那三个树的类如下:
二叉搜索树bst.php:
<?php
/**
* author:zhongjin
* description: 二叉查找树
*/
//结点
class Node
{
public $key;
public $parent;
public $left;
public $right;
public function __construct($key)
{
$this->key = $key;
$this->parent = NULL;
$this->left = NULL;
$this->right = NULL;
}
}
//二叉搜索树
class Bst
{
public $root;
/**
* 初始化树结构
* @param $arr 初始化树结构的数组
* @return null
*/
public function init($arr)
{
$this->root = new Node($arr[0]);
for ($i = 1; $i < count($arr); $i++) {
$this->Insert($arr[$i]);
}
}
/**
* (对内)中序遍历
* @param $root (树或子树的)根节点
* @return null
*/
private function mid_order($root)
{
if ($root != NULL) {
$this->mid_order($root->left);
echo $root->key . " ";
$this->mid_order($root->right);
}
}
/**
* (对外)中序遍历
* @param null
* @return null
*/
public function MidOrder()
{
$this->mid_order($this->root);
}
/**
* 查找树中是否存在$key对应的节点
* @param $key 待搜索数字
* @return $key对应的节点
*/
function search($key)
{
$current = $this->root;
while ($current != NULL) {
if ($current->key == $key) {
return $current;
} elseif ($current->key > $key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
return $current;
}
/**
* 查找树中的最小关键字
* @param $root 根节点
* @return 最小关键字对应的节点
*/
function search_min($root)
{
$current = $root;
while ($current->left != NULL) {
$current = $current->left;
}
return $current;
}
/**
* 查找树中的最大关键字
* @param $root 根节点
* @return 最大关键字对应的节点
*/
function search_max($root)
{
$current = $root;
while ($current->right != NULL) {
$current = $current->right;
}
return $current;
}
/**
* 查找某个$key在中序遍历时的直接前驱节点
* @param $x 待查找前驱节点的节点引用
* @return 前驱节点引用
*/
function predecessor($x)
{
//左子节点存在,直接返回左子节点的最右子节点
if ($x->left != NULL) {
return $this->search_max($x->left);
}
//否则查找其父节点,直到当前结点位于父节点的右边
$p = $x->parent;
//如果x是p的左孩子,说明p是x的后继,我们需要找的是p是x的前驱
while ($p != NULL && $x == $p->left) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 查找某个$key在中序遍历时的直接后继节点
* @param $x 待查找后继节点的节点引用
* @return 后继节点引用
*/
function successor($x)
{
if ($x->right != NULL) {
return $this->search_min($x->right);
}
$p = $x->parent;
while ($p != NULL && $x == $p->right) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 将$key插入树中
* @param $key 待插入树的数字
* @return null
*/
function Insert($key)
{
if (!is_null($this->search($key))) {
throw new Exception('结点' . $key . '已存在,不可插入!');
}
$root = $this->root;
$inode = new Node($key);
$current = $root;
$prenode = NULL;
//为$inode找到合适的插入位置
while ($current != NULL) {
$prenode = $current;
if ($current->key > $inode->key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
$inode->parent = $prenode;
//如果$prenode == NULL, 则证明树是空树
if ($prenode == NULL) {
$this->root = $inode;
} else {
if ($inode->key < $prenode->key) {
$prenode->left = $inode;
} else {
$prenode->right = $inode;
}
}
//return $root;
}
/**
* 在树中删除$key对应的节点
* @param $key 待删除节点的数字
* @return null
*/
function Delete($key)
{
if (is_null($this->search($key))) {
throw new Exception('结点' . $key . "不存在,删除失败!");
}
$root = $this->root;
$dnode = $this->search($key);
if ($dnode->left == NULL || $dnode->right == NULL) { #如果待删除结点无子节点或只有一个子节点,则c = dnode
$c = $dnode;
} else { #如果待删除结点有两个子节点,c置为dnode的直接后继,以待最后将待删除结点的值换为其后继的值
$c = $this->successor($dnode);
}
//无论前面情况如何,到最后c只剩下一边子结点
if ($c->left != NULL) {
$s = $c->left;
} else {
$s = $c->right;
}
if ($s != NULL) { #将c的子节点的父母结点置为c的父母结点,此处c只可能有1个子节点,因为如果c有两个子节点,则c不可能是dnode的直接后继
$s->parent = $c->parent;
}
if ($c->parent == NULL) { #如果c的父母为空,说明c=dnode是根节点,删除根节点后直接将根节点置为根节点的子节点,此处dnode是根节点,且拥有两个子节点,则c是dnode的后继结点,c的父母就不会为空,就不会进入这个if
$this->root = $s;
} else if ($c == $c->parent->left) { #如果c是其父节点的左右子节点,则将c父母的左右子节点置为c的左右子节点
$c->parent->left = $s;
} else {
$c->parent->right = $s;
}
#如果c!=dnode,说明c是dnode的后继结点,交换c和dnode的key值
if ($c != $dnode) {
$dnode->key = $c->key;
}
#返回根节点
// return $root;
}
/**
* (对内)获取树的深度
* @param $root 根节点
* @return 树的深度
*/
private function getdepth($root)
{
if ($root == NULL) {
return 0;
}
$dl = $this->getdepth($root->left);
$dr = $this->getdepth($root->right);
return ($dl > $dr ? $dl : $dr) + 1;
}
/**
* (对外)获取树的深度
* @param null
* @return null
*/
public function Depth()
{
return $this->getdepth($this->root);
}
}
?>
平衡二叉树avl.php:
<?php
/**
* author:zhongjin
* description: 平衡二叉树
*/
//结点
class Node
{
public $key;
public $parent;
public $left;
public $right;
public $bf; //平衡因子
public function __construct($key)
{
$this->key = $key;
$this->parent = NULL;
$this->left = NULL;
$this->right = NULL;
$this->bf = 0;
}
}
//平衡二叉树
class Avl
{
public $root;
const LH = +1; //左高
const EH = 0; //等高
const RH = -1; //右高
/**
* 初始化树结构
* @param $arr 初始化树结构的数组
* @return null
*/
public function init($arr)
{
$this->root = new Node($arr[0]);
for ($i = 1; $i < count($arr); $i++) {
$this->Insert($arr[$i]);
}
}
/**
* (对内)中序遍历
* @param $root (树或子树的)根节点
* @return null
*/
private function mid_order($root)
{
if ($root != NULL) {
$this->mid_order($root->left);
echo $root->key . "-" . $root->bf . " ";
$this->mid_order($root->right);
}
}
/**
* (对外)中序遍历
* @param null
* @return null
*/
public function MidOrder()
{
$this->mid_order($this->root);
}
/**
* 将以$root为根节点的最小不平衡二叉树做右旋处理
* @param $root(树或子树)根节点
* @return null
*/
private function R_Rotate($root)
{
$L = $root->left;
if (!is_NULL($root->parent)) {
$P = $root->parent;
if ($root == $P->left) {
$P->left = $L;
} else {
$P->right = $L;
}
$L->parent = $P;
} else {
$L->parent = NULL;
}
$root->parent = $L;
$root->left = $L->right;
$L->right = $root;
//这句必须啊!
if ($L->parent == NULL) {
$this->root = $L;
}
}
/**
* 将以$root为根节点的最小不平衡二叉树做左旋处理
* @param $root(树或子树)根节点
* @return null
*/
private function L_Rotate($root)
{
$R = $root->right;
if (!is_NULL($root->parent)) {
$P = $root->parent;
if ($root == $P->left) {
$P->left = $R;
} else {
$P->right = $R;
}
$R->parent = $P;
} else {
$R->parent = NULL;
}
$root->parent = $R;
$root->right = $R->left;
$R->left = $root;
//这句必须啊!
if ($R->parent == NULL) {
$this->root = $R;
}
}
/**
* 对以$root所指结点为根节点的二叉树作左平衡处理
* @param $root(树或子树)根节点
* @return null
*/
public function LeftBalance($root)
{
$L = $root->left;
$L_bf = $L->bf;
switch ($L_bf) {
//检查root的左子树的平衡度,并作相应的平衡处理
case self::LH: //新结点插入在root的左孩子的左子树上,要做单右旋处理
$root->bf = $L->bf = self::EH;
$this->R_Rotate($root);
break;
case self::RH: //新节点插入在root的左孩子的右子树上,要做双旋处理
$L_r = $L->right; //root左孩子的右子树根
$L_r_bf = $L_r->bf;
//修改root及其左孩子的平衡因子
switch ($L_r_bf) {
case self::LH:
$root->bf = self::RH;
$L->bf = self::EH;
break;
case self::EH:
$root->bf = $L->bf = self::EH;
break;
case self::RH:
$root->bf = self::EH;
$L->bf = self::LH;
break;
}
$L_r->bf = self::EH;
//对root的左子树作左平衡处理
$this->L_Rotate($L);
//对root作右平衡处理
$this->R_Rotate($root);
}
}
/**
* 对以$root所指结点为根节点的二叉树作右平衡处理
* @param $root(树或子树)根节点
* @return null
*/
public function RightBalance($root)
{
$R = $root->right;
$R_bf = $R->bf;
switch ($R_bf) {
//检查root的右子树的平衡度,并作相应的平衡处理
case self::RH: //新结点插入在root的右孩子的右子树上,要做单左旋处理
$root->bf = $R->bf = self::EH;
$this->L_Rotate($root);
break;
case self::LH: //新节点插入在root的右孩子的左子树上,要做双旋处理
$R_l = $R->left; //root右孩子的左子树根
$R_l_bf = $R_l->bf;
//修改root及其右孩子的平衡因子
switch ($R_l_bf) {
case self::RH:
$root->bf = self::LH;
$R->bf = self::EH;
break;
case self::EH:
$root->bf = $R->bf = self::EH;
break;
case self::LH:
$root->bf = self::EH;
$R->bf = self::RH;
break;
}
$R_l->bf = self::EH;
//对root的右子树作右平衡处理
$this->R_Rotate($R);
//对root作左平衡处理
$this->L_Rotate($root);
}
}
/**
* 查找树中是否存在$key对应的节点
* @param $key 待搜索数字
* @return $key对应的节点
*/
public function search($key)
{
$current = $this->root;
while ($current != NULL) {
if ($current->key == $key) {
return $current;
} elseif ($current->key > $key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
return $current;
}
/**
* 查找树中的最小关键字
* @param $root 根节点
* @return 最小关键字对应的节点
*/
function search_min($root)
{
$current = $root;
while ($current->left != NULL) {
$current = $current->left;
}
return $current;
}
/**
* 查找树中的最大关键字
* @param $root 根节点
* @return 最大关键字对应的节点
*/
function search_max($root)
{
$current = $root;
while ($current->right != NULL) {
$current = $current->right;
}
return $current;
}
/**
* 查找某个$key在中序遍历时的直接前驱节点
* @param $x 待查找前驱节点的节点引用
* @return 前驱节点引用
*/
private function predecessor($x)
{
//左子节点存在,直接返回左子节点的最右子节点
if ($x->left != NULL) {
return $this->search_max($x->left);
}
//否则查找其父节点,直到当前结点位于父节点的右边
$p = $x->parent;
//如果x是p的左孩子,说明p是x的后继,我们需要找的是p是x的前驱
while ($p != NULL && $x == $p->left) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 查找某个$key在中序遍历时的直接后继节点
* @param $x 待查找后继节点的节点引用
* @return 后继节点引用
*/
private function successor($x)
{
if ($x->left != NULL) {
return $this->search_min($x->right);
}
$p = $x->parent;
while ($p != NULL && $x == $p->right) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* (对内)插入结点,如果结点不存在则插入,失去平衡要做平衡处理
* @param $root 根节点 $key 待插入树的数字
* @return null
*/
private function insert_node(&$root, $key)
{
//找到了插入的位置,插入新节点
if (is_null($root)) {
$root = new Node($key);
//插入结点成功
return TRUE;
} else {
//在树中已经存在和$key相等的结点
if ($key == $root->key) {
//插入节点失败
return FALSE;
} //在root的左子树中继续搜索
elseif ($key < $root->key) {
//插入左子树失败
if (!($this->insert_node($root->left, $key))) {
//树未长高
return FALSE;
}
//成功插入,修改平衡因子
if (is_null($root->left->parent)) {
$root->left->parent = $root;
}
switch ($root->bf) {
//原来左右子树等高,现在左子树增高而树增高
case self::EH:
$root->bf = self::LH;
//树长高
return TRUE;
break;
//原来左子树比右子树高,需要做左平衡处理
case self::LH:
$this->LeftBalance($root);
//平衡后,树并未长高
return FALSE;
break;
//原来右子树比左子树高,现在左右子树等高
case self::RH:
$root->bf = self::EH;
//树并未长高
return FALSE;
break;
}
} //在root的右子树中继续搜索
else {
//插入右子树失败
if (!$this->insert_node($root->right, $key)) {
//树未长高
return FALSE;
}
//成功插入,修改平衡因子
if (is_null($root->right->parent)) {
$root->right->parent = $root;
}
switch ($root->bf) {
//原来左右子树等高,现在右子树增高而树增高
case self::EH:
$root->bf = self::RH;
//树长高
return TRUE;
break;
//原来左子树比右子树高,现在左右子树等高
case self::LH:
$root->bf = self::EH;
return FALSE;
break;
//原来右子树比左子树高,要做右平衡处理
case self::RH:
$this->RightBalance($root);
//树并未长高
return FALSE;
break;
}
}
}
}
/**
* (对外)将$key插入树中
* @param $key 待插入树的数字
* @return null
*/
public function Insert($key)
{
$this->insert_node($this->root, $key);
}
/**
* 获取待删除的节点(删除的最终节点)
* @param $key 待删除的数字
* @return 最终被删除的节点
*/
private function get_del_node($key)
{
$dnode = $this->search($key);
if ($dnode == NULL) {
throw new Exception("结点不存在!");
return;
}
if ($dnode->left == NULL || $dnode->right == NULL) { #如果待删除结点无子节点或只有一个子节点,则c = dnode
$c = $dnode;
} else { #如果待删除结点有两个子节点,c置为dnode的直接后继,以待最后将待删除结点的值换为其后继的值
$c = $this->successor($dnode);
}
$dnode->key = $c->key;
return $c;
}
/**
* (对内)删除指定节点,处理该结点往上结点的平衡因子
* @param $node 最终该被删除的节点
* @return null
*/
private function del_node($node)
{
if ($node == $this->root) {
$this->root = NULL;
return;
}
$current = $node;
//现在的node只有两种情况,要么只有一个子节点,要么没有子节点
$P = $current->parent;
//删除一个结点,第一个父节点的平衡都肯定会发生变化
$lower = TRUE;
while ($lower == TRUE && !is_null($P)) {
//待删除结点是左节点
if ($current == $P->left) {
if($current == $node){
if (!is_null($current->left)) {
$P->left = $current->left;
} else {
$P->left = $current->left;
}
}
$P_bf = $P->bf;
switch ($P_bf) {
case self::LH:
$P->bf = self::EH;
$lower = TRUE;
$current = $P;
$P = $current->parent;
break;
case self::EH:
$P->bf = self::RH;
$lower = FALSE;
break;
case self::RH:
$this->RightBalance($P);
$lower = TRUE;
$current = $P->parent;
$P = $current->parent;
break;
}
} //右结点
else {
if($current == $node){
if (!is_null($current->left)) {
$P->right = $current->left;
} else {
$P->right = $current->left;
}
}
$P_bf = $P->bf;
switch ($P_bf) {
case self::LH:
$this->LeftBalance($P);
$lower = TRUE;
$current = $P->parent;
$P = $current->parent;
break;
case self::EH:
$P->bf = self::LH;
$lower = FALSE;
break;
case self::RH:
$P->bf = self::LH;
$lower = TRUE;
$current = $P;
$P = $current->parent;
break;
}
}
}
}
/**
* (对外)删除指定节点
* @param $key 删除节点的key值
* @return null
*/
public function Delete($key)
{
$del_node = $this->get_del_node($key);
$this->del_node($del_node);
}
/**
* (对内)获取树的深度
* @param $root 根节点
* @return 树的深度
*/
private function getdepth($root)
{
if ($root == NULL) {
return 0;
}
$dl = $this->getdepth($root->left);
$dr = $this->getdepth($root->right);
return ($dl > $dr ? $dl : $dr) + 1;
}
/**
* (对外)获取树的深度
* @param null
* @return null
*/
public function Depth()
{
return $this->getdepth($this->root);
}
}
?>
红黑树rbt.php:
<?php
/**
* author:zhongjin
* description: 红黑树
*/
//结点
class Node
{
public $key;
public $parent;
public $left;
public $right;
public $IsRed; //分辨红节点或黑节点
public function __construct($key, $IsRed = TRUE)
{
$this->key = $key;
$this->parent = NULL;
$this->left = NULL;
$this->right = NULL;
//插入结点默认是红色
$this->IsRed = $IsRed;
}
}
//红黑树
class Rbt
{
public $root;
/**
* 初始化树结构
* @param $arr 初始化树结构的数组
* @return null
*/
public function init($arr)
{
//根节点必须是黑色
$this->root = new Node($arr[0], FALSE);
for ($i = 1; $i < count($arr); $i++) {
$this->Insert($arr[$i]);
}
}
/**
* (对内)中序遍历
* @param $root (树或子树的)根节点
* @return null
*/
private function mid_order($root)
{
if ($root != NULL) {
$this->mid_order($root->left);
echo $root->key . "-" . ($root->IsRed ? 'r' : 'b') . ' ';
$this->mid_order($root->right);
}
}
/**
* (对外)中序遍历
* @param null
* @return null
*/
public function MidOrder()
{
$this->mid_order($this->root);
}
/**
* 查找树中是否存在$key对应的节点
* @param $key 待搜索数字
* @return $key对应的节点
*/
function search($key)
{
$current = $this->root;
while ($current != NULL) {
if ($current->key == $key) {
return $current;
} elseif ($current->key > $key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
//结点不存在
return $current;
}
/**
* 将以$root为根节点的最小不平衡二叉树做右旋处理
* @param $root(树或子树)根节点
* @return null
*/
private function R_Rotate($root)
{
$L = $root->left;
if (!is_null($root->parent)) {
$P = $root->parent;
if($root == $P->left){
$P->left = $L;
}else{
$P->right = $L;
}
$L->parent = $P;
} else {
$L->parent = NULL;
}
$root->parent = $L;
$root->left = $L->right;
$L->right = $root;
//这句必须啊!
if ($L->parent == NULL) {
$this->root = $L;
}
}
/**
* 将以$root为根节点的最小不平衡二叉树做左旋处理
* @param $root(树或子树)根节点
* @return null
*/
private function L_Rotate($root)
{
$R = $root->right;
if (!is_null($root->parent)) {
$P = $root->parent;
if($root == $P->right){
$P->right = $R;
}else{
$P->left = $R;
}
$R->parent = $P;
} else {
$R->parent = NULL;
}
$root->parent = $R;
$root->right = $R->left;
$R->left = $root;
//这句必须啊!
if ($R->parent == NULL) {
$this->root = $R;
}
}
/**
* 查找树中的最小关键字
* @param $root 根节点
* @return 最小关键字对应的节点
*/
function search_min($root)
{
$current = $root;
while ($current->left != NULL) {
$current = $current->left;
}
return $current;
}
/**
* 查找树中的最大关键字
* @param $root 根节点
* @return 最大关键字对应的节点
*/
function search_max($root)
{
$current = $root;
while ($current->right != NULL) {
$current = $current->right;
}
return $current;
}
/**
* 查找某个$key在中序遍历时的直接前驱节点
* @param $x 待查找前驱节点的节点引用
* @return 前驱节点引用
*/
function predecessor($x)
{
//左子节点存在,直接返回左子节点的最右子节点
if ($x->left != NULL) {
return $this->search_max($x->left);
}
//否则查找其父节点,直到当前结点位于父节点的右边
$p = $x->parent;
//如果x是p的左孩子,说明p是x的后继,我们需要找的是p是x的前驱
while ($p != NULL && $x == $p->left) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 查找某个$key在中序遍历时的直接后继节点
* @param $x 待查找后继节点的节点引用
* @return 后继节点引用
*/
function successor($x)
{
if ($x->left != NULL) {
return $this->search_min($x->right);
}
$p = $x->parent;
while ($p != NULL && $x == $p->right) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 将$key插入树中
* @param $key 待插入树的数字
* @return null
*/
public function Insert($key)
{
if (!is_null($this->search($key))) {
throw new Exception('结点' . $key . '已存在,不可插入!');
}
$root = $this->root;
$inode = new Node($key);
$current = $root;
$prenode = NULL;
//为$inode找到合适的插入位置
while ($current != NULL) {
$prenode = $current;
if ($current->key > $inode->key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
$inode->parent = $prenode;
//如果$prenode == NULL, 则证明树是空树
if ($prenode == NULL) {
$this->root = $inode;
} else {
if ($inode->key < $prenode->key) {
$prenode->left = $inode;
} else {
$prenode->right = $inode;
}
}
//将它重新修正为一颗红黑树
$this->InsertFixUp($inode);
}
/**
* 对插入节点的位置及往上的位置进行颜色调整
* @param $inode 插入的节点
* @return null
*/
private function InsertFixUp($inode)
{
//情况一:需要调整条件,父节点存在且父节点的颜色是红色
while (($parent = $inode->parent) != NULL && $parent->IsRed == TRUE) {
//祖父结点:
$gparent = $parent->parent;
//如果父节点是祖父结点的左子结点,下面的else与此相反
if ($parent == $gparent->left) {
//叔叔结点
$uncle = $gparent->right;
//case1:叔叔结点也是红色
if ($uncle != NULL && $uncle->IsRed == TRUE) {
//将父节点和叔叔结点都涂黑,将祖父结点涂红
$parent->IsRed = FALSE;
$uncle->IsRed = FALSE;
$gparent->IsRed = TRUE;
//将新节点指向祖父节点(现在祖父结点变红,可以看作新节点存在)
$inode = $gparent;
//继续while循环,重新判断
continue; //经过这一步之后,组父节点作为新节点存在(跳到case2)
}
//case2:叔叔结点是黑色,且当前结点是右子节点
if ($inode == $parent->right) {
//以父节点作为旋转结点做左旋转处理
$this->L_Rotate($parent);
//在树中实际上已经转换,但是这里的变量的指向还没交换,
//将父节点和字节调换一下,为下面右旋做准备
$temp = $parent;
$parent = $inode;
$inode = $temp;
}
//case3:叔叔结点是黑色,而且当前结点是父节点的左子节点
$parent->IsRed = FALSE;
$gparent->IsRed = TRUE;
$this->R_Rotate($gparent);
} //如果父节点是祖父结点的右子结点,与上面完全相反
else {
//叔叔结点
$uncle = $gparent->left;
//case1:叔叔结点也是红色
if ($uncle != NULL && $uncle->IsRed == TRUE) {
//将父节点和叔叔结点都涂黑,将祖父结点涂红
$parent->IsRed = FALSE;
$uncle->IsRed = FALSE;
$gparent->IsRed = TRUE;
//将新节点指向祖父节点(现在祖父结点变红,可以看作新节点存在)
$inode = $gparent;
//继续while循环,重新判断
continue; //经过这一步之后,组父节点作为新节点存在(跳到case2)
}
//case2:叔叔结点是黑色,且当前结点是左子节点
if ($inode == $parent->left) {
//以父节点作为旋转结点做右旋转处理
$this->R_Rotate($parent);
//在树中实际上已经转换,但是这里的变量的指向还没交换,
//将父节点和字节调换一下,为下面右旋做准备
$temp = $parent;
$parent = $inode;
$inode = $temp;
}
//case3:叔叔结点是黑色,而且当前结点是父节点的右子节点
$parent->IsRed = FALSE;
$gparent->IsRed = TRUE;
$this->L_Rotate($gparent);
}
}
//情况二:原树是根节点(父节点为空),则只需将根节点涂黑
if ($inode == $this->root) {
$this->root->IsRed = FALSE;
return;
}
//情况三:插入节点的父节点是黑色,则什么也不用做
if ($inode->parent != NULL && $inode->parent->IsRed == FALSE) {
return;
}
}
/**
* (对外)删除指定节点
* @param $key 删除节点的key值
* @return null
*/
function Delete($key)
{
if (is_null($this->search($key))) {
throw new Exception('结点' . $key . "不存在,删除失败!");
}
$dnode = $this->search($key);
if ($dnode->left == NULL || $dnode->right == NULL) { #如果待删除结点无子节点或只有一个子节点,则c = dnode
$c = $dnode;
} else { #如果待删除结点有两个子节点,c置为dnode的直接后继,以待最后将待删除结点的值换为其后继的值
$c = $this->successor($dnode);
}
//为了后面颜色处理做准备
$parent = $c->parent;
//无论前面情况如何,到最后c只剩下一边子结点
if ($c->left != NULL) { //这里不会出现,除非选择的是删除结点的前驱
$s = $c->left;
} else {
$s = $c->right;
}
if ($s != NULL) { #将c的子节点的父母结点置为c的父母结点,此处c只可能有1个子节点,因为如果c有两个子节点,则c不可能是dnode的直接后继
$s->parent = $c->parent;
}
if ($c->parent == NULL) { #如果c的父母为空,说明c=dnode是根节点,删除根节点后直接将根节点置为根节点的子节点,此处dnode是根节点,且拥有两个子节点,则c是dnode的后继结点,c的父母就不会为空,就不会进入这个if
$this->root = $s;
} else if ($c == $c->parent->left) { #如果c是其父节点的左右子节点,则将c父母的左右子节点置为c的左右子节点
$c->parent->left = $s;
} else {
$c->parent->right = $s;
}
$dnode->key = $c->key;
$node = $s;
//c的结点颜色是黑色,那么会影响路径上的黑色结点的数量,必须进行调整
if ($c->IsRed == FALSE) {
$this->DeleteFixUp($node,$parent);
}
}
/**
* 删除节点后对接点周围的其他节点进行调整
* @param $key 删除节点的子节点和父节点
* @return null
*/
private function DeleteFixUp($node,$parent)
{
//如果待删结点的子节点为红色,直接将子节点涂黑
if ($node != NULL && $node->IsRed == TRUE) {
$node->IsRed = FALSE;
return;
}
//如果是根节点,那就直接将根节点置为黑色即可
while (($node == NULL || $node->IsRed == FALSE) && ($node != $this->root)) {
//node是父节点的左子节点,下面else与这里相反
if ($node == $parent->left) {
$brother = $parent->right;
//case1:兄弟结点颜色是红色(父节点和兄弟孩子结点都是黑色)
//将父节点涂红,将兄弟结点涂黑,然后对父节点进行左旋处理(经过这一步,情况转换为兄弟结点颜色为黑色的情况)
if ($brother->IsRed == TRUE) {
$brother->IsRed = FALSE;
$parent->IsRed = TRUE;
$this->L_Rotate($parent);
//将情况转化为其他的情况
$brother = $parent->right; //在左旋处理后,$parent->right指向的是原来兄弟结点的左子节点
}
//以下是兄弟结点为黑色的情况
//case2:兄弟结点是黑色,且兄弟结点的两个子节点都是黑色
//将兄弟结点涂红,将当前结点指向其父节点,将其父节点指向当前结点的祖父结点。
if (($brother->left == NULL || $brother->left->IsRed == FALSE) && ($brother->right == NULL || $brother->right->IsRed == FALSE)) {
$brother->IsRed = TRUE;
$node = $parent;
$parent = $node->parent;
} else {
//case3:兄弟结点是黑色,兄弟结点的左子节点是红色,右子节点为黑色
//将兄弟结点涂红,将兄弟节点的左子节点涂黑,然后对兄弟结点做右旋处理(经过这一步,情况转换为兄弟结点颜色为黑色,右子节点为红色的情况)
if ($brother->right == NULL || $brother->right->IsRed == FALSE) {
$brother->IsRed = TRUE;
$brother->left->IsRed = FALSE;
$this->R_Rotate($brother);
//将情况转换为其他情况
$brother = $parent->right;
}
//case4:兄弟结点是黑色,且兄弟结点的右子节点为红色,左子节点为任意颜色
//将兄弟节点涂成父节点的颜色,再把父节点涂黑,将兄弟结点的右子节点涂黑,然后对父节点做左旋处理
$brother->IsRed = $parent->IsRed;
$parent->IsRed = FALSE;
$brother->right->IsRed = FALSE;
$this->L_Rotate($parent);
//到了第四种情况,已经是最基本的情况了,可以直接退出了
$node = $this->root;
break;
}
} //node是父节点的右子节点
else {
$brother = $parent->left;
//case1:兄弟结点颜色是红色(父节点和兄弟孩子结点都是黑色)
//将父节点涂红,将兄弟结点涂黑,然后对父节点进行右旋处理(经过这一步,情况转换为兄弟结点颜色为黑色的情况)
if ($brother->IsRed == TRUE) {
$brother->IsRed = FALSE;
$parent->IsRed = TRUE;
$this->R_Rotate($parent);
//将情况转化为其他的情况
$brother = $parent->left; //在右旋处理后,$parent->left指向的是原来兄弟结点的右子节点
}
//以下是兄弟结点为黑色的情况
//case2:兄弟结点是黑色,且兄弟结点的两个子节点都是黑色
//将兄弟结点涂红,将当前结点指向其父节点,将其父节点指向当前结点的祖父结点。
if (($brother->left == NULL || $brother->left->IsRed == FALSE) && ($brother->right == NULL || $brother->right->IsRed == FALSE)) {
$brother->IsRed = TRUE;
$node = $parent;
$parent = $node->parent;
} else {
//case3:兄弟结点是黑色,兄弟结点的右子节点是红色,左子节点为黑色
//将兄弟结点涂红,将兄弟节点的左子节点涂黑,然后对兄弟结点做左旋处理(经过这一步,情况转换为兄弟结点颜色为黑色,右子节点为红色的情况)
if ($brother->left == NULL || $brother->left->IsRed == FALSE) {
$brother->IsRed = TRUE;
$brother->right = FALSE;
$this->L_Rotate($brother);
//将情况转换为其他情况
$brother = $parent->left;
}
//case4:兄弟结点是黑色,且兄弟结点的左子节点为红色,右子节点为任意颜色
//将兄弟节点涂成父节点的颜色,再把父节点涂黑,将兄弟结点的右子节点涂黑,然后对父节点左左旋处理
$brother->IsRed = $parent->IsRed;
$parent->IsRed = FALSE;
$brother->left->IsRed = FALSE;
$this->R_Rotate($parent);
$node = $this->root;
break;
}
}
}
if ($node != NULL) {
$this->root->IsRed = FALSE;
}
}
/**
* (对内)获取树的深度
* @param $root 根节点
* @return 树的深度
*/
private function getdepth($root)
{
if ($root == NULL) {
return 0;
}
$dl = $this->getdepth($root->left);
$dr = $this->getdepth($root->right);
return ($dl > $dr ? $dl : $dr) + 1;
}
/**
* (对外)获取树的深度
* @param null
* @return null
*/
public function Depth()
{
return $this->getdepth($this->root);
}
}
?>
更多关于PHP相关内容感兴趣的读者可查看本站专题:《PHP数据结构与算法教程》、《php程序设计算法总结》、《php字符串(string)用法总结》、《PHP数组(Array)操作技巧大全》、《PHP常用遍历算法与技巧总结》及《PHP数学运算技巧总结》
希望本文所述对大家PHP程序设计有所帮助。
以上是 PHP实现绘制二叉树图形显示功能详解【包括二叉搜索树、平衡树及红黑树】 的全部内容, 来源链接: utcz.com/p/221352.html