图论(graph theory)算法原理、实现和应用全解
上一节讨论了不相交集的实现原理,该数据结构会在本节使用到。图论(graph theory)算法是相当核心的算法,而且图论算法是相当实用的,之前讨论的数据结构,如链表、栈、队列、哈希表都是比较简单的,稍微复杂的是树和堆,本节讨论的图论算法原理和实现则更为复杂,内容也比较多。
图(graph)是一种数据结构,是目前应用最广泛的数据结构,它能实现抽象的功能以及相当生活化的功能,应用范围包括计算机科学、语言学、物理和化学、社会科学、生物学和数学,包括目前热门的人工智能中的神经网络学习。本文涉及相当多的图论算法,包括DFS和BFS、环检测、连通性、拓扑排序、最小生成树、最短路径、最大流网络、图的着色问题等,不过在进入图论的讨论之前,我们先回头说一下数据结构中的逻辑结构和存储结构。
一、数据结构:逻辑结构和存储结构
数据结构是组织数据的方式,例如树,但是要注意数据结构有两种形式:逻辑结构和存储结构,这两种结构在表示一种数据结构的时候不一定完全相同的,逻辑结构是我们分析数据结构和算法的主要形式,而存储结构则是数据结构在内存中的存储形式。
逻辑结构是数据结构的逻辑的表示,同时用于分析数据结构时的形象表示,以后的数据结构设计方式按按照逻辑结构的形式,一般来说,所有的数据结构大部分都是讨论其逻辑结构,算法的操作按照逻辑结构的形式,算法的操作说明也是按照逻辑结构的形式。例如二叉堆的逻辑表示形式为树,但是实现的时候可以使用数组,这里的树就是逻辑形式,数组则是存储结构。逻辑结构又分为线性结构和非线性结构,线性结构例如线性表(数组和链表),栈和队列,非线性结构如树和图。
存储结构是数据结构的实际实现时采取的结构形式,可采取与相应的逻辑结构不同的结构形式,不一定和逻辑结构相同,尽量以简单方便有效率为主,例如不相交集逻辑表示为树,实现的时候使用数组。但是算法的实现还是按照逻辑结构的形式,也就是即使使用数组表示一种数据结构,其操作算法也不一定和常规的数组操作相同。存储结构又分为:顺序结构(数组或顺序表,普通二叉堆使用数组,图可以使用二维数组)、链式结构(链表、栈和队列)、索引结构(树、堆和优先队列)、哈希结构(哈希表、散列结构、不相交集的数组形式是一种散列结构)。
这里的介绍主要是为了明显区分逻辑结构和存储结构,逻辑结构是算法形式上的,存储结构是编程语言上的,在算法理解上,逻辑结构是需要重点关注的,因为描述算法是按照逻辑结构的形式。
二、图的概念和定义
1、图(graph)
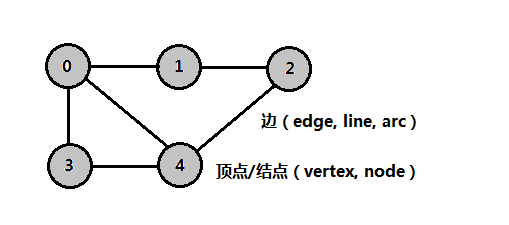
如上图是一个图G,一个图由顶点(vertex)集V和边(edge)集E组成,即G=(V, E),和树类似,其顶点又称为结点,并且边是有意义的,如上图(0,1)称为一条边。
顶点(vertex)的属性:
- 度数(degree),与该顶点相关联的总边数,一个图G的总度数d(V)等于总边数2倍:2E。当图的边具有方向时,一个顶点又分为出度(out-degree)和入度(in-degree),出度是以该顶点为起点的边数,入度是以该顶点为终点的边数。
- 阶数(order),图G中顶点集V的大小为G的阶数。
边又称为线(line)或弧(arc),边(u,v)中表示u和v邻接(adjacent),(u, v) ∈ E,边(edge)的属性:
- 一条边是一个顶点对(u,v),u, v ∈ V,按照图的顶点对是否有序,顶点对有序的图称为有向图(directed graph, digraph),此时边(u,v)和(v,u)是两条不同的边,顶点对无序的图称为无向图(undirected graph),此时边(u,v)和(v,u)是两条相同的边,无向图可看作一个特殊的有向图,下图分别是无向图和有向图的实例:
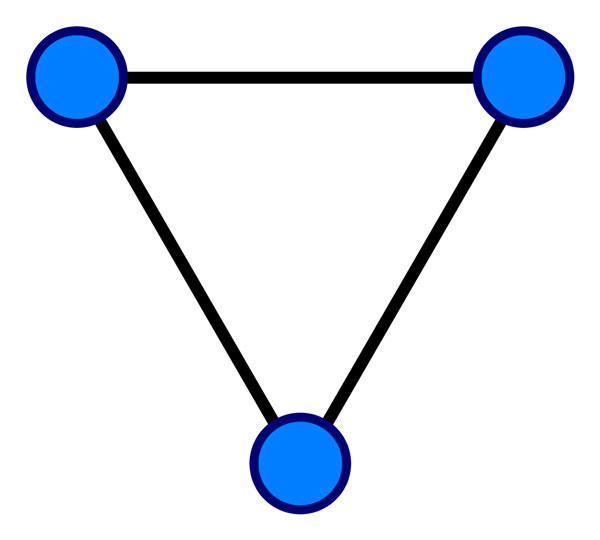
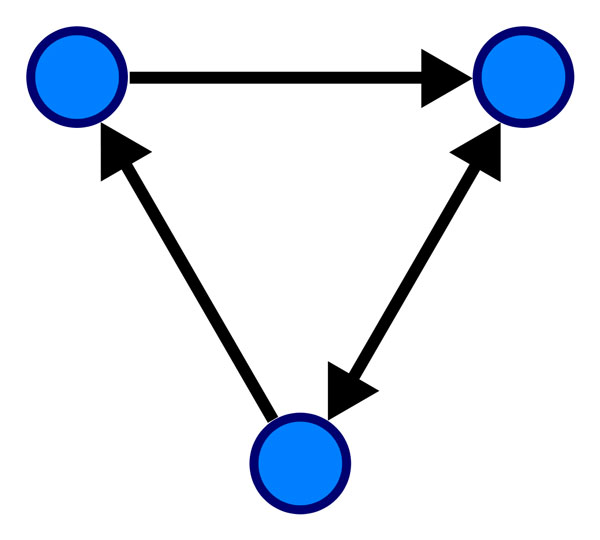
- 具有成分的边包含:权(weight)、值(cost/value),此时图由可分为有权图(weighted graph)和无权图(unweighted graph),无权图可以看作是所有边权值相同的有权图,下面分别是有权图和无权图的实例:
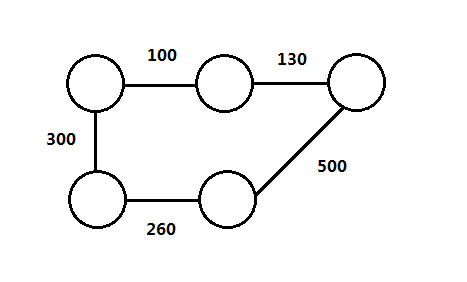
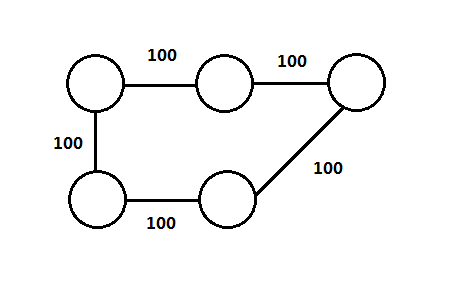
- 路径(path),一条路径是一个顶点序列u1, u2, u3, …, un,(ui, u(i+1)) ∈E,1<=i<n。路径长等于路径的边数:n-1,不包含边的路径长为0。
简单路径:路径上所有顶点互异,起点和终点可以相同,如下图:
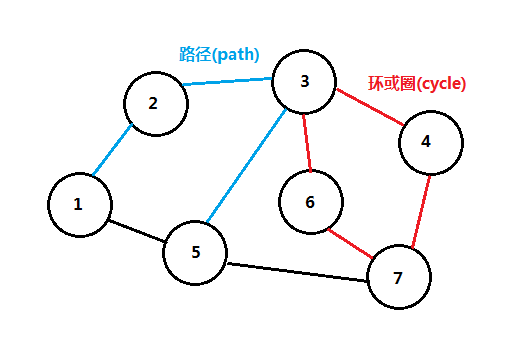
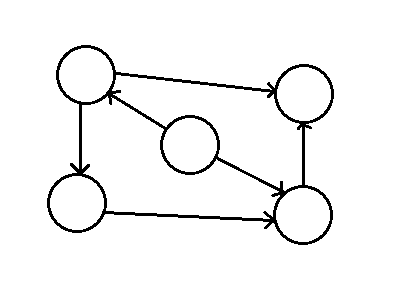
环或圈(cycle),此时u1=un,而且路径长至少为1,有向图(u,v)和(v,u)是一个圈,无向图(u,v)和(v,u)通常不被认为是一个圈。其中无圈图(acyclic graph)中没有圈,无圈有向图又称为DAG(directed acyclic graph),如下图是一个无圈有向图:
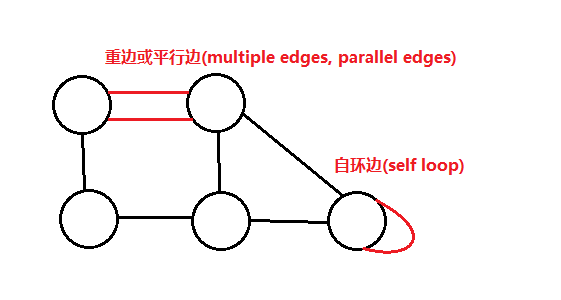
- 自环边(self loop),两个顶点都相同的边。
- 重边或平行边(parallel edges),连接两个顶点的边数超过一条,又称为多重边(multiple
edges),下图是自环边和重边的示例:
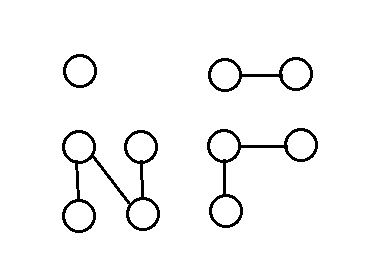
连通图(connected
graph),无向图中每个顶点到任意顶点都存在一条路径,连通的有向图称为强连通(spanly
connected),非连通的有向图,去掉方向其基础图(underlying graph)是连通的,则成为弱连通的(weakly connected),下图是一个非连通图:
完全图(complete
graph),图中任意一对顶点都存在一条边,如下图:
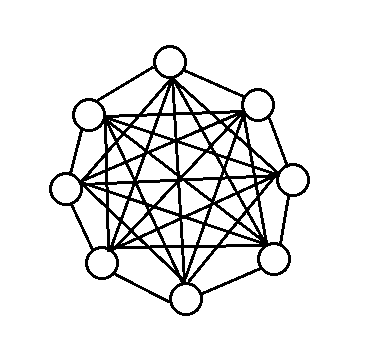
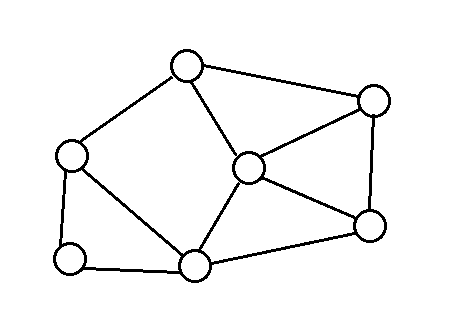
稀疏图(sparse
graph),每个顶点的度数较小的图,如下图:
稠密图(dense
graph),每个顶点的度数较大的图,完全图是稠密图。
2、图的简单应用
图的应用很广泛,这里举几个简单的例子。
航空系统:顶点表示机场,边表示时间、距离或飞行的费用,一般最好有强连通的航空系统,另外常见的需求问题有:求任意两个机场的最佳航线。
交通流:顶点表示街道的交叉口或红绿灯点,边表示速度限度或车辆容量,这时可以求最可能参数交通瓶颈的位置,或找出一条最短路。
社交网络:顶点表示用户,用户的活动、推荐或好友代表边,这样可以表示一个完整的社交用户网络。
电商推荐系统:顶点表示用户已浏览、收藏、购物过等相关的商品,边表示两个商品的相似性,可表示为有权图,权值为相似性的大小。
另外图论又可用于研究物理学和化学中的分子,更多的应用在下面的介绍中会陆续提到。
3、图的数据结构
对于图的数据结构需要考虑两种图:有权图和无权图,无权图不需要考虑边的值相对容易表示,有权图需要适当安排权值的表示。
图的顶点或结点一般用于表示一个事件或物体或实体,拥有可被量化的属性,可设计为拥有完整的数据成员,或仅仅使用部分数据成员。顶点的表示常见有两种:使用关键字(key)表示、使用一个Vertex结构体表示。
使用一个关键字简单表示顶点时,一般使用一个整数标记或名字表示,使用名字表示需要通过散列函数映射到表,需要额外存储顶点的名字和编号,标号从0到V。存储信息过多时,关键字为顶点编号或名字,关键字值为一个数据对象,使用Vertex进行封装,名字过长时或避免重复查找,关键字值可额外存储一个数组指针,该数组指针指向该顶点的邻接表(该顶点邻接的顶点),也就是在Vertex中再存储该顶点所在的邻接表。
使用Vertex结构表示是,这个方式一般是用于无权图,这时可以添加一些主要数据成员或额外的属性,例如:编号或索引i,数据成员data,是否已访问visited,颜色color,到顶点s的距离distance,上一个顶点(父顶点)path,度数degree等等,以后需要使用到的属性都可以添加到Vertex上。
边表示结点或顶点之间的关系,关系是可准确描述的关系,或者是经验上可感知的关系,有成分的边使用权值表示边,代表结点之间关系的量化关系。此时的图是有权图,可以简单用一个Edge结构体表示或使用Pair表示,除了上面提到的属性,可能还会有终点顶点,反向顶点,权值weight,通量或流量capacity。
图论算法中,以边或顶点为基本的操作对象,常见的操作有添加边add_edge或删除边,其实一些基本操作需要按照需要设计。
4、图的表示
图的表示常见有两种方式,但是具体使用哪个表示方式视情况而定,这两个方式分别是邻接矩阵(adjacency matrix)和邻接表(adjacency list),对于一般的需求,邻接表已足够。
对于邻接矩阵,一般是针对稠密图,比如完全图,它使用一个二维数组表示,此时空间需求为V^2,如下图是一个邻接矩阵:
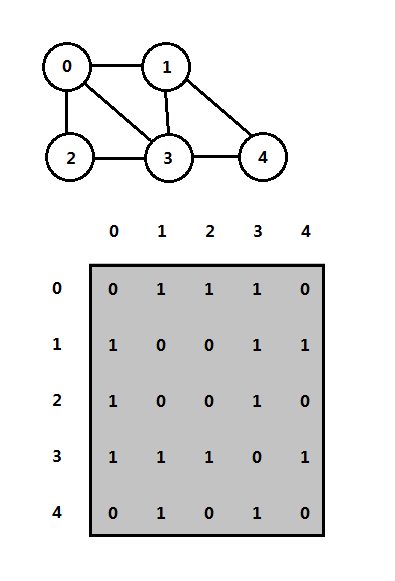
对于A[u][v]=value,表示顶点u和v连接的边,对于无向图value=1表示顶点u和v有一条边连接,同时A[v][u]=1。
对于有向图,value=1表示以u为起点,v为终点的边,对于有权图,value=weight为权值,可以使用很大或很小的权值表示不存在的边,如0、infinity。邻接矩阵删除和插入边时间为O(1)。
图的另一种表示方式是邻接表,一般来说针对稀疏图,针对完全图那和上面的邻接矩阵一样了。该方式使用一个邻接表数组list[V]表示图,也就是对于每个顶点,使用一个表存放与该顶点邻接的所有顶点,一共有V个顶点,空间需求为V+E,邻接表的实例如下图:
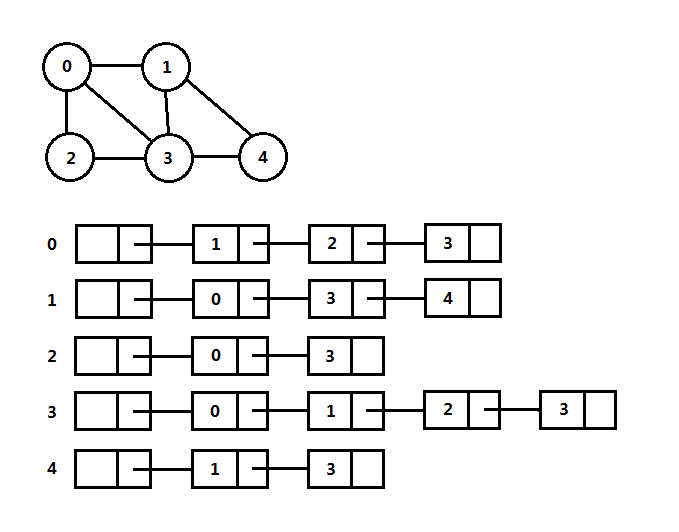
如果边有权值,可以在表中每一个单元额外存储权值信息,可以使用一个Pair结构体表示。
如上图,图G实际是一个邻接表数组,横向存储的顶点是与一个顶点邻接的,该组合为一个邻接表,整体上可以使用一个数组,邻接表根据使用不用的语言实现可以有不同的选择:
- 数组或表,如vector、list,此时允许平行边或重边和自环边,查询时间为O(V),插入时间为O(1);
- 树,tree(stl set),不允许平行边,查询时间和插入时间都为O(logV);
- 散列表,hashtable,无序,不允许平行边,插入查询时间为O(1)。
以上要注意的主要是针对有权图的设计,特别是有权然后还有其它相关属性的时候,那么这时可以使用一个结构体类型表示一个单元。
三、图论遍历算法
图的遍历和树的遍历是类似的,更多内容可查看:树以及遍历算法,里面有对遍历算法的详细介绍。图论遍历算法主要有两种:广度优先遍历(BFS,
breadth first search)和深度优先遍历(DFS, depth first search),这两个遍历算法是下面图论算法的基本形式。
1、图的广度优先遍历(BFS, breadth first search)
BFS时间复杂度为O(V+E),该算法需要使用一个队列辅助存储顶点,以及需要一个访问标记visited,可作为结点成员或使用一个数组,具体使用哪个方式视情况而定。
另外,本文的其它算法还会设计到队列、栈、优先队列、链表等,如果是使用C实现的,需要另外实现,如果是C++或Java那么可以使用现成的相关数据结构,这里不单独给出。
下面实现使用邻接矩阵表示稠密图(也可以不是稠密图),使用BFS遍历该图,首先看一下稠密图的ADT声明:
// 稠密图ADT,顶点为:0 <= x <= v-1typedef struct densegraph{
int v; // 顶点数
int **matrix; // 邻接矩阵
} DenseGraph;
// 稠密图操作声明
extern DenseGraph *dgraph_new(int v);
extern int dgraph_add_edge(DenseGraph *graph, int u, int v);
extern void dgraph_bfs(DenseGraph *graph, int s);
extern int dgraph_clear(DenseGraph *graph);
以上的声明代码比较简单,如果还要更简单你可以直接声明一个二维数组,这里不考虑有权图,考虑的是无权无向图,使用一个visited访问标记数组标记已访问的顶点,这样不会无限循环访问,下面是BFS代码的实现:
int dgraph_add_edge(DenseGraph *graph, int u, int v){ if(graph == NULL || graph->v < 2 || graph->matrix == NULL)
return 0;
graph->matrix[u][v] = 1;
graph->matrix[v][u] = 1;
return 1;
}
static void bfs(DenseGraph *graph, int s){
Queue *queue = queue_new();
int visited[graph->v];
for (int k = 0; k < graph->v; ++k)
visited[k] = 0;
visited[s] = 1;
queue_push(queue, (qdata)s);
int d;
while(!queue_is_empty(queue)){
d = (int)queue_pop(queue);
printf("%d ", (int)d);
for (int i = 0; i < graph->v; ++i)
if(graph->matrix[d][i] && !visited[i]){
visited[i] = 1;
queue_push(queue, (qdata)i);
}
}
queue_clear(queue);
printf("\n");
}
void dgraph_bfs(DenseGraph *graph, int s){
if(graph == NULL || graph->v < 2 || graph->matrix == NULL)
return;
bfs(graph, s);
}
2、广度优先搜索BFS的应用
图论算法中大量使用了BFS或类似的算法,其常见的应用如下:
- 求最短路径路径和最小生成树,两个顶点的最短路径是指两个顶点间含有最少顶点的路径,另外最小生成树也可以使用DFS。
- P2P网络中查找临近的结点,应用场景如P2P文件下载,P2P语音视频通信。
- 搜索引擎的网络爬虫的主要算法之一,DFS也是。
- 社交网络网站,在社交网络中可以搜索k层级以内查找一个人。
- GPS导航系统,使用BFS查找附近地点等。
- 网络广播,在网络中使用BFS将广播包发送给每个节点。
- 垃圾回收算法,例如Cheney算法。
- 无向图环或圈检测,BFS和DFS都可以检测无向图的环或圈,有向图环检测只能使用DFS。
- 查找最大流,如下面会谈到的Ford-Fulkerson算法。
- 检测一个图是否是一个二分图,DFS和BFS都可以。
- 路径查找,使用BFS和DFS检测两个顶点是否有一条路径
- 查找一个顶点到所有可达到的顶点等等。
3、图的深度优先遍历(DFS,depth first search)
DFS的时间复杂度为O(E+V),实现的方式可以使用栈辅助存储顶点,也可以使用递归遍历顶点,类似于树的先序遍历,同样需要使用一个访问标记visited防止重复访问顶点。
这里使用栈实现DFS,实现代码如下:
void sgraph_add_edge(SparseGraph *graph, int u, int v){ if(graph == NULL)
return;
list_push_back(graph->lists[u], (ldata)v);
list_push_back(graph->lists[v], (ldata)u);
}
void sgraph_dfs(SparseGraph *graph, int s){
if(graph == NULL || graph->n < 1 || graph->lists == NULL)
return;
int visited[graph->n];
for (int i = 0; i < graph->n; ++i)
visited[i] = 0;
visited[s] = 1;
List *stack = list_new();
list_push_front(stack, (ldata)s);
int d;
LNode *node;
while(!list_is_empty(stack)){
d = (int)list_front(stack);
printf("%d ", d);
list_pop_front(stack);
node = list_begin(graph->lists[d]);
while(node != NULL){
if(!visited[(int)node->value]){
visited[(int)node->value] = 1;
list_push_front(stack, node->value);
}
node = list_next(graph->lists[d]);
}
}
free(stack);
printf("\n");
}
4、深度优先遍历的应用
DFS和BFS是图论算法的主要算法,其应用非常多,下面是一些常见例子:
- 无权图中求最短路径和最小生成树。
- 检测环或圈。
- 路径查找,使用DFS查找u到v的一条路径,使用栈stack作为辅助,使用递归算法遇到目标顶点v则入栈,后面陆续入栈,打印内容即为所求路径。
- 拓扑排序:计算机中根据作业之间的关系来调度作业(或根据一定先后顺序优先级等);计算机中的指令调度(先后顺序);重新计算公式值公式单元的计算顺序;逻辑合成;makefile编译任务的执行顺序;数据序列化;编译器中的链接器中解决符号依赖关系。
- 检测一个图是否是二分图。
- 查找有向图的强连通分量,后面会详细讨论其实现算法。
- 解决难题,如迷宫问题。
四、图的环或圈检测(cycle detection)
上面提到的BFS和DFS是图论算法的基础,接下来我们开始讨论图论算法的第一个问题:检测一个图中是否含有至少一个环或圈,输入参数为图G,返回值为布尔值0或1。
1、有向图的圈检测
圈检测需要分为有向图和无向图的情况,第一种情况是在有向图中检测圈,有两种方法,首先介绍第一种方法,如下图:
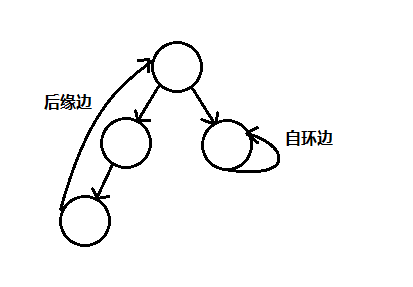
在第一种方法中,如果图中含有后向边(back edge),则含有环,后向边是指以顶点u为起点,u为终点的边(自环边),或者以u为起点,以u的一个祖先顶点为终点的边,算法步骤如下:
- 使用DFS遍历图G;
- 使用一个访问标记visited防止重复访问,使用一个圈标记cycle(或数组),若当前顶点的邻接顶点发现该顶点已被标记为cycle,则含有圈。
注意,首先开始检查点是0到v,将顶点分为visited=1和visited=0的两部分,下一次检查是从visited=0的顶点开始,而cycle标记是在一次DFS中使用,因此处理后需要将cycle置为cycle=0,下面是有圈图的ADT声明代码:
typedef char string[128];typedef struct cnode{ // 边edge
int dest; // 结束顶点
int weight; // 权值
struct cnode *next; // 下一个邻接的顶点
} CNode;
typedef struct cvertex{ // 顶点vertex
int visited; // 访问标记
int cycle; // 一次dfs标记
int src; // 开始顶点
string name; // 顶点的名称
CNode *adjlist; // 该顶点的邻接表
} CVertex;
typedef struct cyclegraph{ // 图graph
int n; // 顶点数量
int is_directed; // 是否为有向图
CVertex *list; // 邻接表数组(顶点数组)
} CycleGraph;
extern CycleGraph *cgraph_new(int n, int is_directed);
extern void cgraph_add_edge(CycleGraph *graph, const char uname[], const char vname[], int u, int v, int w);
extern void cgraph_dfs(CycleGraph *graph, int s);
extern void cgraph_bfs(CycleGraph *graph, int s);
// 使用一般DFS方式检测有向图是否有圈
extern int cgraph_is_cyclic_directed_normal(CycleGraph *graph);
// 使用着色的方式检测有向图是否有圈
extern int cgraph_is_cyclic_directed_color(CycleGraph *graph);
// 一般方式检测无向图是否有圈
extern int cgraph_is_cyclic_undirected_normal(CycleGraph *graph);
// 使用不相交集检测无向图是否有圈
extern int cgraph_is_cyclic_undirected_disjset(CycleGraph *graph);
extern int cgraph_clear(CycleGraph *graph);
上面是一份标准的图ADT的声明方式,可以在实际开发中使用,若要简单起见,可以直接使用一个list数组和顶点的编号即可。CVertex中的name是顶点的名称,在可视化分析中可能会使用到,若要更复杂的数据形式,可以扩充该string类型。下面是第一种在无向图中检测圈的算法实现:
static int is_cyclic_directed_normal(CycleGraph *graph, int u){ if(!graph->list[u].visited){
graph->list[u].visited = 1;
graph->list[u].cycle = 1;
CNode *node = graph->list[u].adjlist;
while(node != NULL){
if(!graph->list[node->dest].visited && is_cyclic_directed_normal(graph, node->dest))
return 1;
else if(graph->list[node->dest].cycle)
return 1;
node = node->next;
}
}
graph->list[u].cycle = 0;
return 0;
}
int cgraph_is_cyclic_directed_normal(CycleGraph *graph){
if(graph == NULL)
return 0;
for (int i = 0; i < graph->n; ++i)
graph->list[i].visited = 0;
for (int j = 0; j < graph->n; ++j)
if(is_cyclic_directed_normal(graph, j))
return 1;
return 0;
}
第二种在无向图中检测圈的算法是使用着色检测,着色就是给顶点或给边着色,这里是给顶点着色(后面会有详细介绍),算法步骤描述如下:
- 使用DFS对无向图进行遍历;
- 使用红绿蓝三种颜色,使用一个颜色数组color[V]或者在顶点上添加一个color属性,每个顶点初始化为红色;
- 遍历顶点u,在遍历u的邻接顶点之前先染为绿色;
- 遍历邻接顶点时,如果找到绿色的顶点,则存在环;如果是红色的,继续递归调用;
- 遍历完成后,u染为蓝色。
注意在以上染色算法中不用使用visited访问标记,因为蓝色可以标记为已访问,上面是一次DFS的算法,需要检测以任意顶点开始的圈,下一次检测时只需要从红色顶点开始,下面是该算法的实现:
static int is_cyclic_directed_color(CycleGraph *graph, int u){ graph->list[u].color = 2;
CNode *node = graph->list[u].adjlist;
while(node != NULL){
if(graph->list[node->dest].color == 2)
return 1;
else if(graph->list[node->dest].color == 1 && is_cyclic_directed_color(graph, node->dest))
return 1;
node = node->next;
}
graph->list[u].color = 3;
return 0;
}
int cgraph_is_cyclic_directed_color(CycleGraph *graph){
if(graph == NULL)
return 0;
for (int i = 0; i < graph->n; ++i)
graph->list[i].color = 1;
for (int j = 0; j < graph->n; ++j)
if(graph->list[j].color == 1)
if(is_cyclic_directed_color(graph, j))
return 1;
return 0;
}
2、无向图的圈检测
使用不相交集中的并查算法可以检测一个无向图中是否含有圈,这个相关原理已经在上一节中谈论到:并查算法和环检测,下面是该算法的实现:
int cgraph_is_cyclic_undirected_disjset(CycleGraph *graph){ if(graph == NULL || graph->is_directed)
return 0;
CNode *node;
Disjset *disjset = disjset_new(graph->n);
for (int j = 0; j < graph->n; ++j)
graph->list[j].visited = 0;
for (int i = 0; i < graph->n; ++i) {
node = graph->list[i].adjlist;
graph->list[i].visited = 1;
while(node != NULL){
if(!graph->list[node->dest].visited && disjset_union(disjset, i, node->dest))
return 1;
node = node->next;
}
}
disjset_clear(disjset);
return 0;
}
另外还有一种简单的方法,同样是使用DFS,并且使用visited访问标记,设顶点u,u 的上一个顶点为parent(第一个顶点的parent为-1),如果u的邻接顶点v已被访问,并且v不等于parent,则含有圈,实现代码如下:
static int is_cyclic_undirected_normal(CycleGraph *graph, int u, int parent){ graph->list[u].visited = 1;
CNode *node = graph->list[u].adjlist;
while(node != NULL){
if(!graph->list[node->dest].visited){
if(is_cyclic_undirected_normal(graph, node->dest, u))
return 1;
}
else if(node->dest != parent)
return 1;
node = node->next;
}
return 0;
}
int cgraph_is_cyclic_undirected_normal(CycleGraph *graph){
if(graph == NULL || graph->is_directed)
return 0;
for (int i = 0; i < graph->n; ++i)
graph->list[i].visited = 0;
for (int j = 0; j < graph->n; ++j)
if(!graph->list[j].visited && is_cyclic_undirected_normal(graph, j, -1))
return 1;
return 0;
}
以上介绍的检测图是否有环或圈的算法在实际中已基本够用,其主要操作是使用visited进行标记,当进行一趟DFS在已经visited的顶点中找不到圈,则下一趟从未被visited的顶点开始找。
五、拓扑排序(topological sorting)
图的拓扑排序主要是针对有向无圈图(DAG)的排序,对于所有有向边uv,顶点u先于v,排序的时候u在前,v在后(如果图有圈,那么拓扑排序是不可能的,因为此时u先于v同时v又先于u,也就是遇到找不到没有入边的顶点),实质是实现一种先后顺序的排列,如下图:
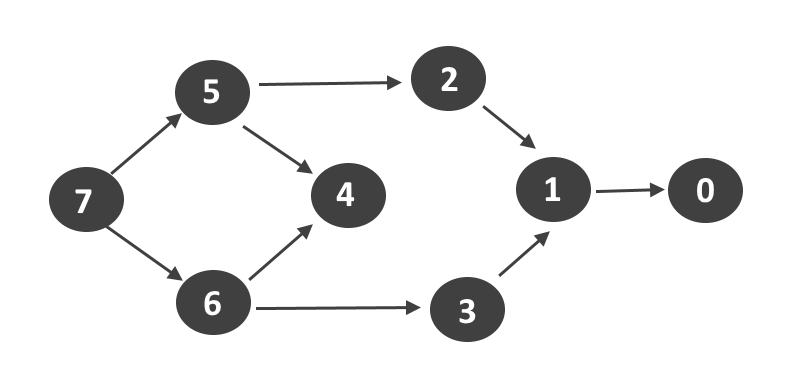
首先,找出一个没有入边的顶点(任意),该顶点作为第一个顶点,之后重复之前的操作直到排序完成。因为找到没有入边的顶点可能有多个,所以拓扑排序并不是唯一的,上图的其中一个拓扑排序为:7、6、5、4、3、2、1、0。
拓扑排序是比较有用的,尽管其实质是实现一种先后顺序,下面先讨论两个实现拓扑排序的算法(基本形式离不开DFS和BFS),以及求所有的拓扑排序,然后讨论拓扑排序的一些常见应用。
1、拓扑排序的实现算法
首先介绍第一种算法,该算法使用BFS,其中需要添加顶点的入度数indegree,使用一个队列,将入度为0的顶点入队,之后出队处理,将邻接的顶点的入度数相应减1,时间为O(V+E),实现代码如下:
void graph_topsort_01(Graph *graph){ if(graph == NULL || !graph->is_directed)
return;
List *list = list_new();
Queue *queue = queue_new();
for (int i = 0; i < graph->n; ++i) {
if (graph->list[i].indegree == 0)
queue_push(queue, &graph->list[i]);
}
Vertex *v;
Node *node;
int count = 0;
while(!queue_is_empty(queue)){
v = queue_pop(queue);
count++;
list_push_back(list, v);
node = graph->list[v->src].adjlist;
while(node != NULL){
if(--graph->list[node->dest].indegree == 0)
queue_push(queue, &graph->list[node->dest]);
node = node->next;
}
}
if(count != graph->n){
printf("cycle found.\n");
perror("cycle found in topological sorting");
queue_clear(queue);
list_clear(list);
return;
}
LNode *n = list_begin(list);
while(n != NULL){
printf("[%d] ", ((Vertex*)(n->value))->src);
n = list_next(list);
}
printf("\n");
queue_clear(queue);
list_clear(list);
}
第二个算法则更简单,其时间为O(V+E),直接使用DFS,遍历每个顶点,使用一个栈,将顶点陆续入栈。从任意一个顶点开始遍历(后序入栈),如果该顶点没有入边,则该顶点会先于所有后代顶点出栈,也就是实现了先后顺序的排列;如果该顶点有入边,那么该顶点也会先于后代出栈,并且其祖先及其分支都会在栈顶部分,这也是实现了先后顺序的排列,下面是实现算法:
static int topsort_02(Graph *graph, List *stack, int u){ graph->list[u].visited = 1;
graph->list[u].cyclic = 1;
Node *node = graph->list[u].adjlist;
while(node != NULL){
if(!graph->list[node->dest].visited)
return topsort_02(graph, stack, node->dest);
else if(graph->list[node->dest].cyclic){
printf("cycle found.\n");
return 0;
}
node = node->next;
}
list_push_front(stack, &graph->list[u]);
graph->list[u].cyclic = 0;
return 1;
}
void graph_topsort_02(Graph *graph){
if(graph == NULL || !graph->is_directed)
return;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].visited = 0;
graph->list[i].cyclic = 0;
}
List *stack = list_new();
for (int j = 0; j < graph->n; ++j) {
if(!graph->list[j].visited)
if(!topsort_02(graph, stack, j))
break;
}
if(stack->size != graph->n){
list_clear(stack);
return;
}
LNode *n = list_begin(stack);
while(n != NULL){
printf("[%d] ", ((Vertex*)(n->value))->src);
n = list_next(stack);
}
printf("\n");
list_clear(stack);
}
2、求DAG的所有拓扑排序
上面所求的是一个无权DAG的一种拓扑排序,当DAG是一个有权图时,我们可以通过找出一个最优的拓扑排序(最大或最小权值)。从0到V遍历顶点,选择未访问并且入度为0的顶点,这里使用回溯算法,例如访问第0个顶点,如果有2个分支,在遍历邻接顶点时,处理第1个邻接顶点并进行递归调用,递归完成再恢复,实现算法如下:
static void all_topsort(Graph *graph, List *list){ int flag = 0;
Node *node;
for (int i = 0; i < graph->n; ++i) {
if(graph->list[i].indegree == 0 && !graph->list[i].visited){
node = graph->list[i].adjlist;
while(node != NULL){
graph->list[node->dest].indegree--;
node = node->next;
}
list_push_back(list, &graph->list[i]);
graph->list[i].visited = 1;
all_topsort(graph, list);
node = graph->list[i].adjlist;
while(node != NULL){
graph->list[node->dest].indegree++;
node = node->next;
}
list_pop_back(list);
graph->list[i].visited = 0;
flag = 1;
}
}
if(!flag){
LNode *n = list_begin(list);
while(n != NULL){
printf("[%d] ", ((Vertex*)n->value)->src);
n = list_next(list);
}
printf("\n");
}
}
void graph_all_topsort(Graph *graph){
if(graph == NULL || !graph->is_directed)
return;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].visited = 0;
}
List *list = list_new();
all_topsort(graph, list);
list_clear(list);
}
3、拓扑排序的应用
拓扑排序主要用于任务调度,按先后顺序进行排序,应用包括计算机指令调度,指令为顶点,有方向表示按顺序执行;公式计算,顶点为公式计算的各个部分,重新计算时,按照每个部分的先后顺序进行计算;逻辑合成,逻辑运算的先后顺序;数据序列化;编译器中链接器的符号依赖关系,顶点为符号,使用一个符号,该符号可能依赖于其它符号。
六、最短路径算法(shortest path algorithm)
最短路径算法的问题是求顶点u到顶点v的最短路径长,求解这个问题需要考虑三种情况:有权图、无权图和有负边的情况。在有权图中,路径u=v1,v2,v3,…,vn=v,最短路径一般指的是顶点u到顶点v的最小权值和,也就是1到n-1顶点的所有边权值相加。在无权图中,则是顶点u到顶点v的路径最小边数,也就是n-1。
具有负值权值的边叫做负边,如下图是一个带有负边的图:
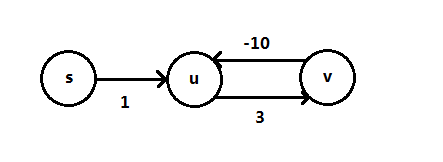
具有负值边的图最短路径是不确定的,没有负值边时,s到s的最短路径为0,如果u到v经过负值边,循环形成一个负值圈,则说该图带有负值圈,如下图是一个带有负值圈的图:
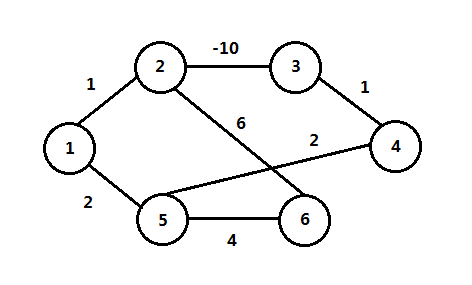
常见的最短路径问题是单源最短路径问题,也就是单个起始点s,从s到G中其它顶点的最短路径,也就是求最短路径树(shortest path tree),输入为有权图G=(V, E)。需要考虑的情况有:无权图、有权图、有负边、有负值圈(负边有圈)以及所有点对的最短路径。
1、无权最短路径算法
该问题是求s到G中其它顶点的最短路径,针对的是无权图,无权图是有权图的特殊情况,例如可以设每条边的权值为1。该算法使用的是BFS,使用的数据成员包括dist(到s的距离)、path(顶点v的上一个顶点),打印最短距离使用DFS,该算法使用邻接表时间为O(V+E),实现算法如下:
void graph_shortest_path_unweighted(Graph *graph, int s){ if(graph == NULL || s < 0)
return;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].path = -1;
graph->list[i].dist = INT_MAX;
}
Queue *queue = queue_new();
graph->list[s].dist = 0;
queue_push(queue, &graph->list[s]);
Node *node;
Vertex *v;
while(!queue_is_empty(queue)){
v = queue_pop(queue);
node = graph->list[v->src].adjlist;
while(node != NULL){
if(graph->list[node->dest].dist == INT_MAX){
graph->list[node->dest].dist = v->dist + 1;
graph->list[node->dest].path = v->src;
queue_push(queue, &graph->list[node->dest]);
}
node = node->next;
}
}
free(queue);
}
2、Dijkstra算法
该算法主要针对有权图,并且无负边,当然也可以用于上面无权图的情况,但是该算法一般最差时间为O(V^2),使用优先队列时间为O(ElogV),Dijkstra算法类似于无权最短路径算法,它是一个贪婪算法,循环找出一个未被访问的最小距离顶点x,x.visited=1,若邻接顶点为访问则进行处理更新距离,其中使用到基于顶点到s的距离构造的最小堆,对优先队列和堆不了解的朋友可以查看:优先队列和堆的原理和实现,下面是该算法的具体实现:
void graph_shortest_path_weighted_dijkstra(Graph *graph, int s){ if(graph == NULL || s < 0)
return;
BinaryHeap *heap = bheap_new(graph->n);
for (int i = 0; i < graph->n; ++i) {
graph->list[i].visited = 0;
graph->list[i].path = -1;
graph->list[i].dist = INT_MAX;
bheap_push(heap, graph->list[i].dist, &graph->list[i]);
}
graph->list[s].dist = 0;
bheap_decrease(heap, &graph->list[s], graph->list[s].dist);
Vertex *v = NULL;
Node *node;
while(1){
v = bheap_pop(heap);
if(v == NULL)
break;
v->visited = 1;
node = graph->list[v->src].adjlist;
while(node != NULL){
if(!graph->list[node->dest].visited){
if(v->dist + node->weight < graph->list[node->dest].dist){
graph->list[node->dest].dist = v->dist + node->weight;
bheap_decrease(heap, &graph->list[node->dest], v->dist + node->weight);
graph->list[node->dest].path = v->src;
}
}
node = node->next;
}
}
bheap_clear(heap);
}
3、具有负值边的图
针对具有负值边的图,使用邻接表时该算法时间为O(E*V),该算法使用BFS,在更新邻接顶点y的时候,若y不在队列中则将y入队,整体和上面的无权最短路径算法类似,其中具有负值圈会导致无限循环,为了避免这种情况,我们可以通过标记一个顶点在队列中出现的次数,如果出现了V+1次则跳出循环,实现代码如下:
void graph_shortest_path_weighted_negative(Graph *graph, int s){ if(graph == NULL || s < 0)
return;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].dist = INT_MAX;
graph->list[i].path = -1;
}
int times[graph->n];
for (int j = 0; j < graph->n; ++j)
times[j] = 0;
Queue *queue = queue_new();
graph->list[s].dist = 0;
queue_push(queue, &graph->list[s]);
Node *node;
Vertex *v;
while(!queue_is_empty(queue)){
v = queue_pop(queue);
node = graph->list[v->src].adjlist;
while(node != NULL){
if(v->dist + node->weight < graph->list[node->dest].dist){
graph->list[node->dest].dist = v->dist + node->weight;
graph->list[node->dest].path = v->src;
if(!queue_has(queue, &graph->list[node->dest])){
if(++times[node->dest] == graph->n + 1)
break;
queue_push(queue, &graph->list[node->dest]);
}
}
node = node->next;
}
}
queue_clear(queue);
}
4、无圈图的最短路径
对于无圈图的情况可以使用上面的无权最短路径或针对有权图的Dijkstra算法,在无圈图中,按照拓扑顺序选取顶点,例如选取顶点v后,该顶点没有其它visited=0的顶点发出的进入边,也就是路径一直是向前的(否则就有圈了)。对于无权图仍然可以使用无权最短路径算法,对于有权图则可以改进Dijkstra算法,无圈的有权图则是相当于有方向了(有向无圈图),可以直接使用基于BFS类似的无权最短路径算法,其时间为O(E+V)。
无圈图可以用于模拟下坡滑雪的问题,由上而下滑雪显然不会有圈,或者是不可逆的化学反应,顶点表示实验的特定状态,边表示从一个状态到另一个状态的转变,边的权值表示释放的能量,因为状态的改变导致能量释放,因此图是无圈的。
关键路径分析法
关键路径问题一般和时间相关,上面是关键路径呢?在一个无圈图中,从开始顶点s到结束顶点n,假设边为耗费时间t,可能有几种最短路径(最少时间),规定完成时间为T,关键路径是指那些完成时间刚好是T的路径(也就是松弛时间为0)。
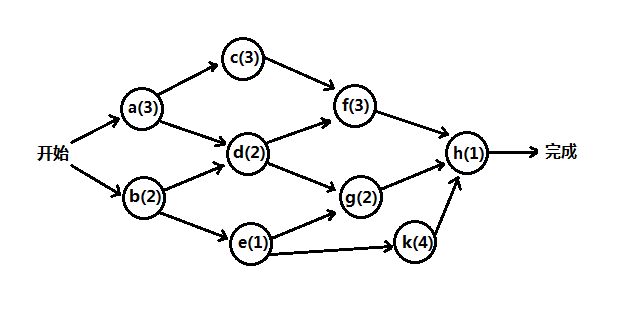
如上图是一个动作结点图,顶点表示执行的动作及其完成的花费时间,形式如a(t1)->b(t2),边表示优先关系,边(u,v)表示动作u必须在v开始前完成执行,因而是无圈图。假设互不依赖的动作可以并行地执行,即所有的动作都需要执行完成,另一种类似的问题是事件结点图。
这里的问题是:a、求最早完成时间;b、哪些动作可延迟,及其可延迟时长(而不影响最短完成时间)。
首先我们需要将上面的动作结点图转为一个有权无圈图:a(t1)->b(t2)转为1->(a/t1)->2->(b/t2),1、2是两个动作,动作的开始和结束用顶点表示,动作的耗时使用边表示,由于两个动作顶点需要两条边,因此可能需要额外插入哑边和哑顶点(也就是权值为0的边和空顶点),如下图:
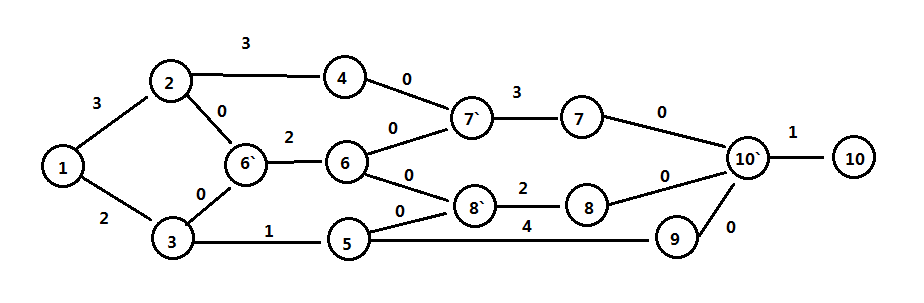
最早完成时间:求第一个顶点到最后一个顶点的最长路径,因为是无圈图,所以不受正值圈的影响(类似负值圈),使用类似最短路径算法计算,计算法则为:
- 第1个顶点的完成时间为0;
- 顶点u到v的时间为Ev=max(Du+w),Ev是到v的最早完成时间,Du是起点到u的完成时间,w是u到v的时间。
最迟完成时间是指每个动作能够完成,又不影响最后的完成时间的最晚时间,可通过翻转拓扑顺序来计算,计算法则为:
- 第V个顶点(最后一个)的最迟完成时间等于最早完成时间Tv;
- 当前顶点为v,所有上一个顶点统称为u,t为所有u到v的完成时间,u的最早完成时间为Lu=min(Tv-t)。
松弛时间表示动作可被延迟但不影响整体完成的时间量,计算法则:边(u,v)的松弛时间为Lv-Eu-Tuv,Tuv表示u到v的完成时间。
关键路径:指松弛时间为0的边为关键性的动作,至少存在一条完全是0松弛时间的路径,称为关键路径。
5、所有点对的最短路径
该问题要求找出所有顶点对之间的最短路径,也就是任意顶点对(u,v)之间的最短路径,而上面给出的算法是针对单源路径:一个顶点到其它顶点的最短路径,求解该问题可以通过运行V次单源路径算法求得,不使用优先队列的Dijkstra算法时间为O(V^3),使用优先队列则为O(V*ElogV),对于稀疏图来说,该方法更快,对于稠密图可使用另外的方法,下一节会讨论到。
七、最大网络流问题(maximum flow problem)
给定一个有向图G=(V,E),边(u,v)的流容量为C(uv),可表示为谁管通过的水量,或一条马路通过的交通流量,对于每条边最多有C(uv)个单位的流可通过,C为变的最大容量,如下图:
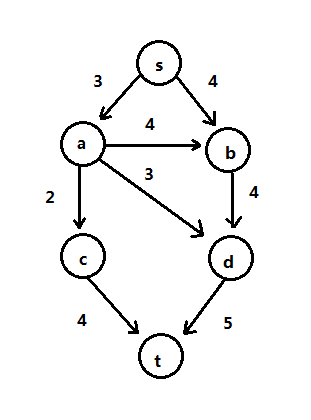
图的最大流是指:给定发点s,收点t,任意顶点进入的流等于发出的流(除了s和t),进入边的流不能超过边的最大容量,图的最大流为从发点s发出的流的和,如下图是上图可通过的最大流:
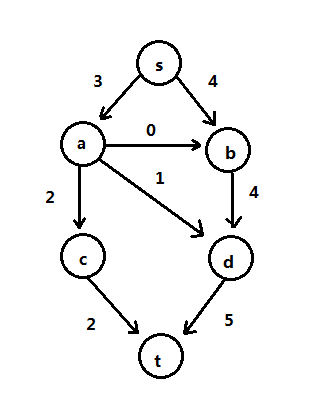
最大网络流问题是:确定从s到t可通过的最大流网络,也就是可通过的最大流图。下面介绍两个算法,Ford-Fulkerson算法和Dinic算法,其算法基本逻辑是:先确定s到t是否有一条路径(使用BFS),再来计算最大流。
1、Ford-Fulkerson算法
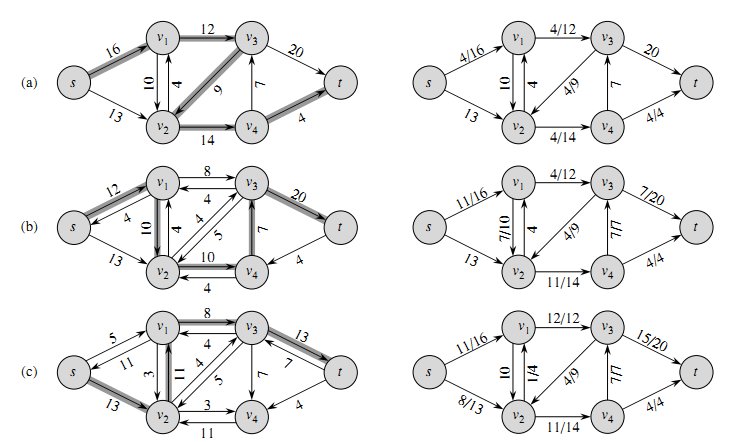
首先介绍残留图(residual
graph)Gr,Gr是和原图G同样的图,不同的是,Gr每条边表示还能使用的流数,使用e表示残留边的流数,Gf表示已使用的流,Ge表示原图每条边的容量,则e=Ge-Gf。进行一次计算最大流的时候需要检查e的大小,当e=0时表示该边不能再通过流了。
该算法的详细步骤如下:
- 初始化最大流max_flow=0,新建一个和G一样的残留图Gr,或者给顶点增加一个e属性表示残留边的流数;
- 循环使用BFS检查Gr从s到t是否存在一条路径:find_path(Gr,s,t),使用path和visited标记,不存在则返回max_flow;
- 如果存在路径,则在Gr中从t到s使用DFS计算一条路径的最大流,flow=INT_MAX,flow=min(flow,e);
- 更新Gr中边的容量,边的原方向上:Gr(u,v) -= flow,边的反方向上:Gr(v,u) += flow;
- max_flow
+= flow,循环第(2)步,直到s到t不再存在路径。
该算法的一般最差时间为O(EV^3),不过优化该算法可以降低最差时间,首先我们可以优先选择最大增长的增长通路,时间为O(E^2logVlogP),P为最大边容量,此时在使用BFS检查路径的时候,应该使用有权最大路径算法Dijkstra和优先队列。
另一种优化的方法是优先选择最少边数的路径,时间为O(VE^2),此时在使用BFS检查路径的时候使用无权最短路径算法。
Ford-Fulkerson算法实现代码如下:
int graph_max_flow_fordfulkerson(Graph *graph, int s, int t){ if(graph == NULL || !graph->is_directed || s < 0 || t < 0)
return INT_MIN;
Node *node;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].path = -1;
graph->list[i].visited = 0;
node = graph->list[i].adjlist;
while(node != NULL){
node->flow = node->weight;
node = node->next;
}
}
int max_flow = 0, flow = 0, v;
while(find_path(graph, s, t)){
flow = INT_MAX;
v = t;
while(v != s){
flow = min(flow, edge_weight(graph, graph->list[v].path, v));
v = graph->list[v].path;
}
v = t;
while(v != s){
update_flow_positive(graph, graph->list[v].path, v, flow);
update_flow_negative(graph, v, graph->list[v].path, flow);
v = graph->list[v].path;
}
max_flow += flow;
}
release_negative_edge(graph);
return max_flow;
}
2、Dinic算法
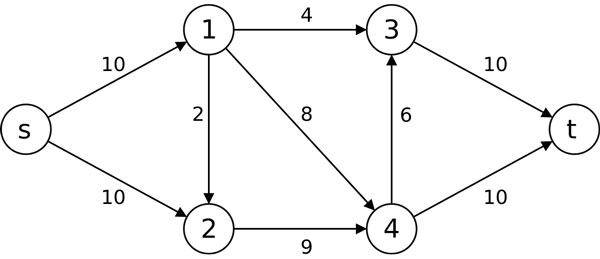
Dinic算法比上面的算法更快,时间为O(EV^2),该图同样使用残留图Gr(具有正反向的边),在使用BFS确定s到t是否有路径的时候,同时构建一个层次图(level graph),根据各个顶点到s的最短路径一次给顶点标记(或者增加使用一个数组记录记录每个顶点的出发边数),这样的后面使用该层次图进行计算最大流,按层次进行计算,该算法的实现如下:
// DFSstatic int send_max_flow(Graph *graph, int flow, int u, int t){
if(u == t)
return flow;
Node *node = graph->list[u].adjlist;
int min_flow, temp_flow;
while(node != NULL){
if(node->flow > 0 && graph->list[node->dest].level == graph->list[u].level + 1){
min_flow = min(flow, node->flow);
temp_flow = send_max_flow(graph, min_flow, graph->list[node->dest].src, t);
if(temp_flow > 0){
node->flow -= temp_flow;
update_flow_negative(graph, node->dest, u, temp_flow);
return temp_flow;
}
}
node = node->next;
}
return 0;
}
int graph_max_flow_dinic(Graph *graph, int s, int t){
if(graph == NULL || !graph->is_directed || s < 0 || t < 0 || s == t)
return INT_MIN;
Node *node;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].path = -1;
graph->list[i].visited = 0;
node = graph->list[i].adjlist;
while(node != NULL){
node->flow = node->weight;
node = node->next;
}
}
int max_flow = 0, flow = 0;
while(find_path_dinic(graph, s, t)){
while((flow = send_max_flow(graph, INT_MAX, s, t)) != 0)
max_flow += flow;
}
release_negative_edge(graph);
return max_flow;
}
以上两个算法的源码中BFS的部分以及其它辅助部分不贴出来,后面有提供github的完整源码地址,需要详细的源码请到后面查看github的项目地址。
另外,对于图的最大网络流问题的应用,例如给定一个交通量限制,最大化交通运输量;或者是计算机网络之间的数据传输,最大化数据包流,它最大的特定是假设有起点s和收点t,并且假设有流动方向的。
八、最小生成树(minimum spanning tree)
一个图G的最小生成树是连接G内所有顶点的边构成的树,其边权值相加最小。最小生成树不唯一,树的边数为V-1,并且该树是无圈的,它包含G内所有顶点,如下图是图G及其最小生成树:
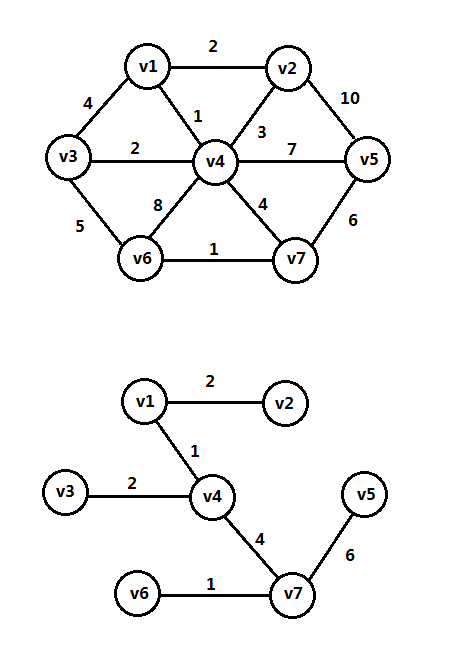
求最小生成树一般来说针对的是无向图(有向图也可以,但比较困难),并且要求图G是连通的,最小生成树存在当且仅当G是连通的,算法的实现需要预先检查G是否是连通的。
最小生成树的应用例如电路板设计,房子电路安装,使用最小的电线等,下面介绍求最小生成树的两个常见算法:Prim算法和Kruskal算法,这两个算法都是贪婪算法,针对连通、无向、有权、非负边的图。
1、Prim算法
该算法和Dijkstra算法是相同的(针对无向图),对于稠密图的情况其时间复杂度为O(V^2),对于稀疏图使用二叉堆时其时间复杂度为O(ElogV)。
Prim算法实现方式和Dijkstra算法类似,但有两个不同,d为连接到顶点u的最短边权值,而path为导致d改变的最后顶点(邻接顶点),其它部分大体类似,Prim算法的实现如下:
void graph_mst_prim(Graph *graph){ if(graph == NULL || graph->is_directed || !graph_undirected_is_connected(graph))
return;
BinaryHeap *heap = bheap_new(graph->n);
for (int i = 0; i < graph->n; ++i) {
graph->list[i].visited = 0;
graph->list[i].path = -1;
graph->list[i].d = INT_MAX;
bheap_push(heap, graph->list[i].d, &graph->list[i]);
}
graph->list[0].visited = 1;
graph->list[0].path = 0;
graph->list[0].d = 0;
bheap_decrease(heap, &graph->list[0], graph->list[0].d);
Vertex *v = NULL;
Node *node;
while(1){
v = bheap_pop(heap);
if(v == NULL)
break;
v->visited = 1;
node = graph->list[v->src].adjlist;
while(node != NULL){
if(!graph->list[node->dest].visited){
if(node->weight < graph->list[node->dest].d){
graph->list[node->dest].d = node->weight;
bheap_decrease(heap, &graph->list[node->dest], node->weight);
graph->list[node->dest].path = v->src;
}
}
node = node->next;
}
}
bheap_clear(heap);
}
2、Kruskal算法
该算法的时间复杂度为O(ElogV),Kruskal算法主要是使用了不相交集的union-find算法,按照最小的权选择边,当所选的边在MST中不会产生圈时则选择改边。选择最小权的边,则是按照边的权值对边进行排序,可以使用快速排序,或使用最小堆将E条边放入堆中,对E条边进行循环处理,从堆中取出最小边E(u,v),检查u和v是否属于同一个集合,存在表明有圈则不选择改边,不存在则选择改边,并进行合并,Kruskal算法的具体实现如下:
void graph_mst_kruskal(Graph *graph, Node *edges[]){ if(graph == NULL || graph->is_directed || !graph_undirected_is_connected(graph))
return;
BinaryHeap *heap = bheap_new(2 * graph->e);
Node *node;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].path = -1;
node = graph->list[i].adjlist;
while(node != NULL){
bheap_push(heap, node->weight, node);
node = node->next;
}
}
Disjset *disjset = disjset_new(graph->n);
int count = 0;
while(count < graph->n - 1){
node = bheap_pop(heap);
if(!disjset_union(disjset, node->src, node->dest)){
edges[count] = node;
count++;
}
}
bheap_clear(heap);
disjset_clear(disjset);
}
3、最小生成树的应用
最小生成树的应用比较广泛,它的实质是求图的最小权值和,应用主要是以下几个方面:
- 网络设计,包括电话布线,电气分布设计,水力系统布局,电视电缆布线,计算机网络设计(求数据传输的最小负载或耗时),公路设计等。
- NP困难问题的近似解法,例如巡回售货员问题(traveling
salesman problem)。
- 聚类分析,k聚类问题可以看作是找出一个MST,并删除k-1条最大边。
- 间接应用,包括最宽路径问题(widest path problem),LDPC纠错码(低密度奇偶校验码),用Renyi熵进行图像校准,进行实时人脸验证时学习显著特征,减少蛋白质中氨基酸序列的数据存储,模拟粒子相互作用的局部性模型,以太网桥接的自动配置协议,以避免网络中的循环。
九、DFS的应用和图的连通性
DFS也就是深度优先搜索算法,实现该算法可以使用递归访问或使用栈辅助,同时使用visited标记已访问的顶点,对于不连通的图需要重新检查未被访问的顶点。
1、无向图
对于无向图,如果一个图是连通的,那么从任一顶点开始使用DFS可以访问到每一个结点,如果图是不连通的,则找出每个连通分支,将算法应用到每个分支上。使用DFS访问无向图,会接触每条边两次:uv和vu,也就是接触每个链接表一次。
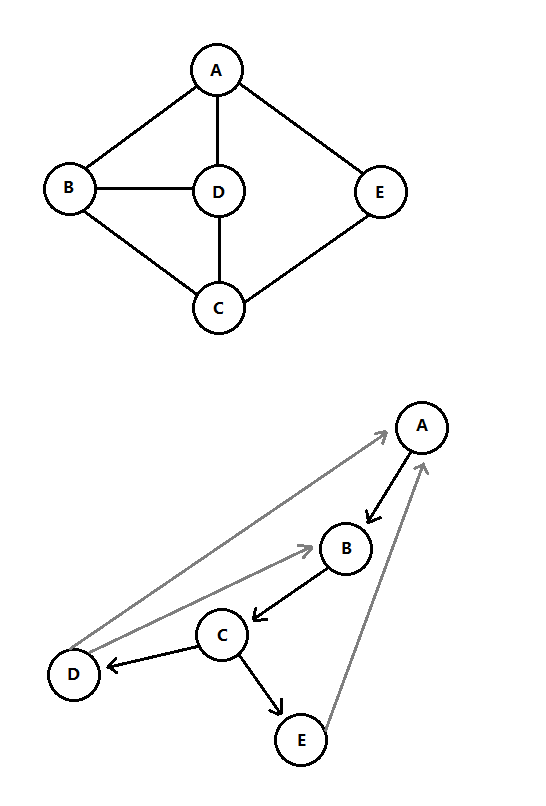
如上图第一个是图G,第二个是图G的深度优先生成树(或DFS树),该树模拟执行的DFS遍历,显示顶点被标记的顺序。DFS树的大体生成过程如下:从u开始遍历到v,如果v未被访问,则用一条有向边表示;到v遍历u的时候,u已被访问,则用虚线边(或灰色边表示,如上图),称为背向边,背向边本身不属于树的一部分。非连通的图生成的DFS树集合称为DFS生成森林。
2、双连通性
如果一个连通的无向图中不存在删除之后图不再连通的顶点,则该图是双连通的。双连通性的应用例如计算机网络,若该网络是双连通的,则任意一台计算机出故障不影响该网络的正常工作,又如公共运输系统,如果该运输网络是双连通的,则任一个站点被破坏,则还可以选择其它站点和路径。
如果一个连通的图中,删除某些顶点则使图不再连通,这些点称为割点(articulation point),如下图C和D都是割点:
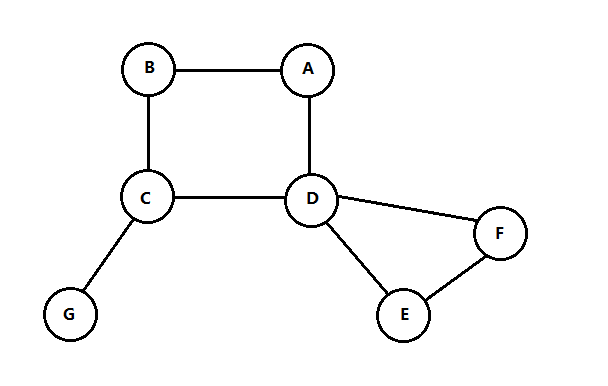
对割点的检测也是比较重要的,DFS提供一种算法以线性时间找出图中的割点,下面是找出连通图中的割点(注意,该算法需要保证图是连通的),下面是找出连通图中的割点的算法步骤:
- 首先生成对于图G的DFS树。
- 对于顶点v指定一个先序编号I(v),该编号是执行DFS先序遍历的时候给每个顶点指定的编号。
- 顶点v的最低编号顶点L(v),该编号是一个顶点的编号(可能是自身的或其它顶点的),L(v)是以下三个数的最小值:a、I(v),自身的编号;从背向边中找,与v邻接的所有背向边(v,w)的最低值I(w);从非背向边中找,与v邻接的所有边的最低L(w)。
- 割点的判断规则,在DFS中:如果根结点的儿子多于1个,则根结点是割点;对于非根结点,如果I(v) <= L(w),则该结点是割点。
该算法的时间复杂度和DFS复杂度一样,为O(E+V),上面具有割点的图的DFS树如下:
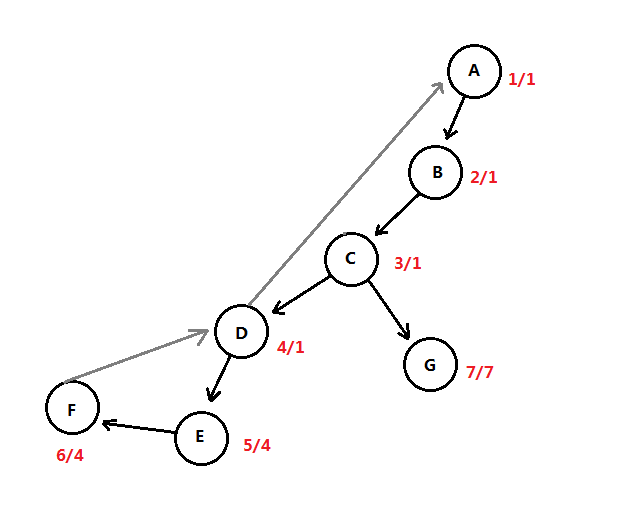
红色的标记中,左边的是该结点执行DFS时的I(v)编号(也可以从0开始),右边是最低顶点编号L(v),该DFS树的根是A,只有一个儿子,因而不是割点。结点B的L(v)是经过结点D回到A因此L(v)=1。对于非根结点若I(v)<=L(w),w是v的邻接边,对于C顶点I(C)=3 < L(G)=7,因此C是割点,检测割点的算法实现如下:
static void find_articulation_p(Graph *graph, List *list, int u, int *counter, int *root, int *r){ graph->list[u].visited = 1;
Node *node = graph->list[u].adjlist;
graph->list[u].low = graph->list[u].num = (*counter)++; // 1 初始化编号
while(node != NULL){
if(!graph->list[node->dest].visited){ // 向前的边
graph->list[node->dest].path = node->src;
find_articulation_p(graph, list, node->dest, counter, root, r); // DFS
if(node->src == *r)
(*root)++;
if(graph->list[node->dest].low >= graph->list[u].num){
if(node->src == *r){
if(*root >= 2)
list_push_back(list, &graph->list[u]);
}
else
list_push_back(list, &graph->list[u]);
}
graph->list[u].low = min(graph->list[u].low, graph->list[node->dest].low); // 3
}
else if(graph->list[u].path != node->dest) // 背向边
graph->list[u].low = min(graph->list[u].low, graph->list[node->dest].num); // 2
node = node->next;
}
}
List *graph_find_articulation_p(Graph *graph){
if(graph == NULL || graph->is_directed)
return NULL;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].visited = 0;
graph->list[i].path = -1;
}
int counter = 0, r = 0, root = 0;
List *list = list_new();
find_articulation_p(graph, list, r, &counter, &root, &r);
return list;
}
3、欧拉回路
欧拉回路来源于柯尼斯堡七桥问题,欧拉在1736年解决了该问题,一般来说该问题是图论的开端。欧拉回路是指:从图中的一个顶点出发恰好访问每条边一次回到原点,也就是求该路径,找出一个圈,该圈刚好经过每条边回到原点,该问题又称为一笔画问题,起点等于终点的欧拉回路需要满足:图G是连通的;每个顶点的度数为偶数。
和欧拉回路相似的另一个问题叫做欧拉环游,又称为欧拉路径,也就是:访问图中的每一条边一次,但最后不一定回到起点的路径,存在欧拉路径需要满足条件:奇数度的顶点个数为2个,其它都为偶数;奇数度的顶点小于2个或多于2个都不存在。
欧拉回路的算法步骤大体如下:
- 找出含有未访问的边的路径上的第一个顶点v;
- 从v出发执行DFS直到回到v,将得到的路径和已存在的路径进行合并;
- 找出下一个顶点重复执行以上操作。
该算法复杂度可达到O(E+V),具体实现这里就不给出了。和欧拉回路相似的还有一个问题:哈密顿问题,它是在无向图中找出一个圈,使得该圈通过图中的所有顶点,该问题没有已知的有效算法,它是一个NP完全问题。
4、有向图
在有向图中执行DFS也可以生成DFS生成森林,其中里面不包含在树中的边包括:背向边,不包含在树中的前向边,交叉边(把不相关的两个顶点连接起来)。DFS在有向图中的其中一个应用是:检测一个有向图是否是无圈图,上面已经提供了一些算法,使用DFS树时,当且仅当它没有背向边图G则没有圈。也可以使用拓扑排序检测,拓扑排序检测的另一种方式:在DFS森林中使用后序遍历给顶点指定编号,编号有序的表示图是无圈图,否则是有圈图。
5、查找强分支
图的强分支是指图的强连通分支,查找一个有向图的强连通分支,可以通过使用两次DFS实现,其算法步骤如下:
- 在图G上执行一次DFS,使用后序遍历对顶点编号,再把G的所有边反向,形成Gr;
- 在Gr上执行一次DFS,总是从最高的顶点开始(编号最大),每一轮遍历结果得到一个强连通分支;
- 得到强连通分支,每个强连通分支是一个顶点子集,可能只有一个顶点或多个顶点。
十、NP完全性(NP-complete)
一般来说,我们之前介绍的算法其时间都是多项式时间(polynomial time),因为它们要解决的问题(problem)相当比较简单,但是还存在其他大量重要的问题,它们在复杂度上大体等价,这些问题称为NP-完全(NP-complete)问题,这些问题或者都有多项式时间解法,或者都没有多项式时间解法,问题的变种解法,可能不知道线性解法,也不知道多项式时间的解法。例如上面提到的哈密尔顿问题,找一个简单圈,包含图中的每个顶点,或者是求有向图的无权单源最长路径等。
1、问题的难与易
对于容易的问题,一般的问题将运行时间考虑成输入数据的量的方式,花费的时间对于输入数据的量而言是线性的。存在一些真正的难题,难到不可能解出来,这些不可能的问题称为不可判定问题(undecidable problem),一些特殊的不可判定的问题称为停机问题(halting
problem),例如,使Java编译器不仅能检查语法,还能检查所有无限循环的程序,但是该程序可能很难检查它自己,这些问题又称为递归不可判定的(recursively undecidable)。
2、NP类
NP类问题稍逊于不可判定问题,也就是说这类问题还是有解的,NP(nondeterministic polynomial-time)称为非确定型多项式时间。检验一个问题是否属于NP,可以将该问题用“是/否(yes/no)“的语言描述,如果在多项式时间内能证明一个问题的”是”的实例为正确,则该问题属于NP类,这里不用担心”否”的实例,因为程序总是会进行正确的选择。
NP类包含所有多项式时间解的问题,解本身包含了验证方法,下面会有更详细的介绍,另外不是所有的可判定问题都属于NP,例如检查一个图是否没有哈密尔顿圈。
3、NP-complete和P、NP、NP-Hard问题
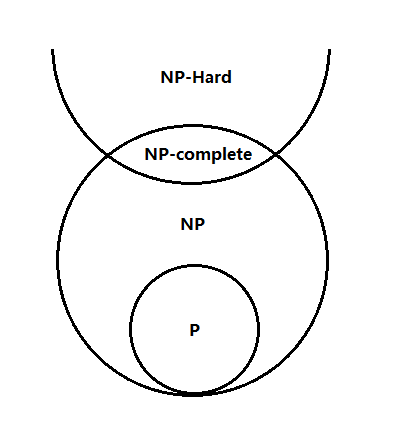
NP所有问题的子集叫做NP-完全问题,它是NP中最难的问题,NP的任一问题都能以多项式时间归约成NP-完全问题,第一个被证明是NP-完全的问题是可满足性(statisfiability)问题,该问题可以和其它所有的NP-完全问题进行转换求解。
常见的NP完全问题有:可满足性问题、哈密尔顿回路问题、巡回售货员问题、最长路径问题、装箱(bin packing)问题、背包(knapsack)问题、图的着色(graph coloring)问题和团(clique)问题等等,这些问题都可以通过和可满足性问题进行转换而求解。
对于问题x的分类:设需要解决的问题为x,问题的解为y,以及求解时间t:
- P(Polynomial)类问题,x为多项式时间问题,也就是P问题,也就是x可以在P时间内得到解决。
- NP(Nondeterministic Polynomial-time)类问题,这类问题的x是不确定型多项式时间问题,如果能在P时间内验证y是x的解的问题则是NP问题,这个也就是证明x是NP问题的方法。NP问题有可能可以在P时间内解决,也就是一个问题x有可能同时是P和NP。
- NP-complete问题,它是NP问题的一个子集,这类问题没办法在P时间内解决,但可以在P事件内验证y是x的解。并且所有的NP-complete问题都可以在P时间内互相转换,这也就是说,如果你碰到一个NP-complete问题,可以通过找到已知的一个NP-complete问题的解法进行求解。
x <=p M表示问题x在P时间内转换为M,x和M是两个NP-complete问题,这两个问题可以互相转换(关于转换的例子可以查一下和3-SAT问题的转换),证明x是NP-complete的方法是:如果能够在P时间内将其它NPC转为x,则x是NP-complete。
- NP-Hard问题,NP-complete问题也是NP-Hard问题的子集,这里问题可以在P时间内互相转换。
下面介绍一个相对更有机会碰到的问题:图的着色问题,该问题属于NP-complete问题,NP-complete问题不是没有解,而是解一般可能是指数解,也就是不存在多项式解,通过一些特别的方式可能大体得到一些P时间的解,但一般不是最优解。
十一、图的着色问题(graph coloring problem)
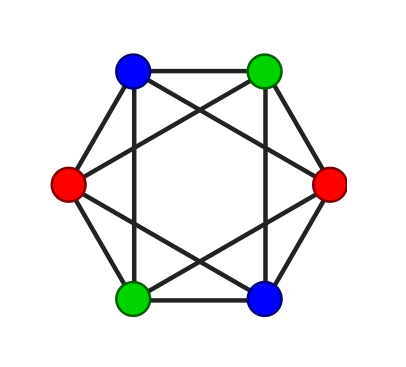
图的着色问题是这样的:给定一个约束,分配特定的颜色到图中的特定元素,也就是给元素着色,图的着色实质是给顶点或边进行分类或约束或标记。根据着色的元素的不同,图的着色又可分为以下三类:
- 顶点着色(vertex coloring):给定m个颜色,在图G中找出一种着色方式,使任意邻接的两个顶点的颜色都不相同。
- 边着色(edge coloring):任意一个顶点关联的边中,任意两条边的颜色都不同。
- 面着色(face coloring):又称为地图着色,面着色可转为顶点着色。
着色数(chromatic
number):给一个图G着色使用的最少颜色数称为该图的着色数,找出一个图G的着色数属于NP-complete问题。
1、图着色的应用
图着色的应用比较多,相对会常遇到,其中一些常见的例子如下:
- 制定计划或时间表,给定科目和学生,同一个学生可能同时修几个科目,若要按科目进行考试,如何安排最少时间使得每个学生能在每个科目都能考试。可以使用图的着色进行解决,顶点表示科目,边表示两个科目共有的学生,图的顶点着色数等于考试安排的最少时间段数。
- 移动射频分配,频率分配到塔上,同一个地点不能分配相同的频率,求最少分配的频率数。顶点表示每个塔,边表示每个塔在彼此的范围内(也就是在同一个地点的范围),可用顶点着色,求其着色数。
- 数独问题,数独是在9×9的格子里,每个3×3表示一块,有9块,找出每一行、每一列、每一块均含1-9的数字,不重复。这里使用顶点着色,这里的颜色数指定为9个,顶点表示每个格子,如果每个顶点在同一行或同一列或同一块,则有一条边。
- 寄存器分配,在编译器优化中,将目标程序的大量变量分配到有限的CPU寄存器上,在程序的一个执行段内,同一个寄存器不能分配给两个或以上的变量。顶点表示变量,边表示在程序的一个执行段内的两个变量的连线,使用顶点着色,颜色数最大为CPU的寄存器数。
- 二分图,使用两种颜色可以检测一个图是否是二分图,如果图可使用两种颜色着色,则是二分图,这里使用顶点着色。
- 地图着色,地图上任意相邻的国家或地区不能分配相同的颜色,使用四种颜色足以给任何一张地图上色。
- 计算机网络部署更新,给一个网络上的计算机安装一些更新,同一时间不能占用两台计算机,使用顶点着色,顶点表示计算机,边表示同时在运行的计算机的连线,着色数表示有几种部署更新的方式,或足够时间内部署更新的次数。
2、基本贪婪着色算法
该贪婪算法不保证能解出最小着色数,但可以保证着色数的一个上界,该着色数不会超过d+1,其中d是图G的顶点最大度数,该算法的复杂度为O(V^2+E),另外还有一个更快的Welsh-Powell算法时间为O(V^2),着色步骤如下:
- 使用第一个颜色给第一个顶点着色;
- 在余下的V-1个顶点中执行以下步骤:
在当前已选的顶点v中,使用于v邻接的顶点未使用的最小颜色给v着色,若v的邻接顶点已用完之前的颜色,则分配一个新的颜色给v。
该着色算法的实现如下:
void graph_coloring_greedy(Graph *graph){ if(graph == NULL)
return;
int available[graph->n];
for (int i = 0; i < graph->n; ++i) {
graph->list[i].color = -1;
available[i] = 0;
}
graph->list[0].color = 0;
Node *node;
int c;
for (int j = 1; j < graph->n; ++j) {
node = graph->list[j].adjlist;
while(node != NULL){
if(graph->list[node->dest].color != -1)
available[graph->list[node->dest].color] = 1;
node = node->next;
}
for (c = 0; c < graph->n; ++c) {
if(!available[c])
break;
}
graph->list[j].color = c;
node = graph->list[j].adjlist;
while(node != NULL){
if(graph->list[node->dest].color != -1)
available[graph->list[node->dest].color] = 0;
node = node->next;
}
}
}
3、m着色问题
该问题是检查图G是否可以用最多m个颜色进行着色,满足任意两个顶点的颜色不相同。算法的输入为图G,输出为顶点着色的结果,如果不能最多使用m个颜色则返回false,该问题可用回溯算法解决,步骤如下:
- 使用递归算法,从顶点v开始,循环使用m个颜色检查v的邻接顶点是否已存在某个颜色;
- 使用邻接顶点未使用的颜色进行着色;
- 选择下一个v+1顶点递归处理;
- 当v=G.size时递归结束。
该算法的实现如下:
static int is_safe(Graph *graph, int u, int c){ Node *node = graph->list[u].adjlist;
while(node != NULL){
if(graph->list[node->dest].color == c)
return 0;
node = node->next;
}
return 1;
}
static int m_coloring(Graph *graph, int m, int u){
if(graph->n == u)
return 1;
for (int c = 0; c < m; ++c) {
if(is_safe(graph, u, c)){
graph->list[u].color = c;
if(m_coloring(graph, m, u + 1))
return 1;
graph->list[u].color = 0;
}
}
return 0;
}
int graph_m_coloring(Graph *graph, int m){
if(graph == NULL || m < 0)
return 0;
for (int i = 0; i < graph->n; ++i) {
graph->list[i].color = 0;
}
if(!m_coloring(graph, m, 0)){
printf("solution does not exist");
return 0;
}
graph_print_color(graph);
return 1;
}
4、给有圈图着色
该问题是比较简单的,规律如下:顶点数为偶数的有圈图着色数为2,顶点数为奇数的有圈图着色数为3。
5、图的边着色
上面的问题都是属于顶点着色,这里给一个边着色的例子,边着色是一个顶点相关的任意两条边颜色都不同,该问题不存在多项式时间求解,但存在求着色数的最优解的近似值,算法步骤如下:
- 使用BFS遍历G;
- 选择一个v,将不同的颜色分配给关联边,将这些边标记为已着色;
- 从v的一条边开始遍历;
- 使用新的顶点重复上述步骤,直到所有边已着色。
边着色由于应用不是特别明显,也不是很广泛,这里就不给出具体的实现了。以上所有的图论算法的完整源码可在下面的github项目中查看:
https://github.com/onnple/graphtheory
十二、图的应用
在物理、生物、社会和信息系统中,图可以用来建模许多类型的关系和过程。许多实际问题可以用图来表示。
为了强调它们在现实世界系统中的应用,网络这个术语有时被定义为一个图,其中的属性(如名称)与顶点和边相关联,而将现实世界系统表示为网络并将其理解为网络的学科被称为网络科学。
1、计算机科学
在计算机科学中,图被用来表示通信网络、数据组织、计算设备、计算流程等。例如,一个网站的链接结构可以用一个有向图表示,其中顶点表示网页,有向边表示从一个页面到另一个页面的链接。类似的方法可以应用于社交媒体、旅行、生物学、计算机芯片设计、绘制神经退行性疾病进展、和许多其他领域。因此,开发处理图的算法是计算机科学的主要兴趣。图的变换通常是形式化的,用图重写系统表示。与侧重于基于规则的图内存操作的图转换系统相辅相成的是面向事务安全、持久存储和查询图结构数据的图数据库,如Neo4j
2、语言学
各种形式的图论方法已证明在语言学中特别有用,因为自然语言常常适合于离散结构。传统上,语法和组合语义遵循基于树的结构,其表达能力取决于组合原则,在层次图中建模。更现代的方法,如头驱短语结构语法,使用类型化特征结构对自然语言的语法建模,这些特征结构是有向无环图。在词汇语义学中,特别是在计算机上,当一个给定的单词被相关的单词理解时,建模单词的意义就更容易了;因此,语义网络在计算语言学中非常重要。尽管如此,音系学中的其他方法(例如,使用格点图的最优性理论)和形态学(例如,使用有限状态形态学,使用有限状态传感器)在语言作为图的分析中也很常见。事实上,这一数学领域对语言学的有用性催生了一些组织,如TextGraphs项目,如WordNet、VerbNet等。
3、物理和化学
图论也被用来研究化学和物理中的分子。在凝聚态物理中,通过收集与原子拓扑有关的图论性质的统计量,可以定量地研究复杂的模拟原子结构的三维结构。此外,“费曼图和计算规则将量子场论总结成一种与人们想要理解的实验数字密切相关的形式。”在化学中,图是分子的自然模型,顶点表示原子,边表示键。这种方法特别用于分子结构的计算机处理,从化学编辑器到数据库搜索。在统计物理学中,图可以表示系统相互作用部分之间的局部连接,以及系统上物理过程的动态。类似地,在计算神经科学中,图可以用来表示大脑区域之间的功能连接,这些区域相互作用产生各种认知过程,其中顶点代表大脑的不同区域,而边缘代表这些区域之间的连接。图论在电气网络的电气建模中起着重要的作用,在这里,权值与线段的电阻有关,从而获得网络结构的电气特性。用图表示多孔介质的微尺度通道,其中顶点表示孔隙,边表示连接孔隙的较小通道。化学图论利用分子图作为分子模型的一种方法。
4、社会科学
社会学中的图论:莫雷诺社会图(1953)图论也被广泛地应用于社会学中,作为一种衡量演员声望或探索谣言传播的方法,特别是通过使用社会网络分析软件。在社交网络的保护伞下,有许多不同类型的图。熟人图和友谊图描述了人们是否互相认识。影响图是一种模型,用来描述某个人是否能够影响其他人的行为。最后,协作图建模两个人是否以特定的方式一起工作,例如一起在电影中表演。
5、生物学
同样,图论在生物学和保护工作中也很有用,其中一个顶点可以表示某些物种存在(或栖息)的区域,而边缘则表示这些区域之间的迁移路径或移动。当观察繁殖模式或跟踪疾病、寄生虫的传播或运动的变化如何影响其他物种时,这些信息非常重要。图论也被用于连接学;神经系统可以被看作是一个图,其中节点是神经元,边缘是它们之间的连接。
6、数学
在数学中,图形在几何学和拓扑的某些部分如结理论中是有用的。代数图论与群论有着密切的联系。代数图论已经应用于包括动态系统和复杂性在内的许多领域。
7、其他应用
可以通过为图的每条边分配一个权重来扩展图结构。带有权值的图,或称加权图,用于表示成对连接具有某些数值的结构。例如,如果一个图表示一个道路网络,那么权值可以表示每条道路的长度。每条边可能有几个相关的权重,包括距离(如前一个示例中所示)、旅行时间或货币成本。这种加权图通常被用于GPS和旅行计划搜索引擎的程序中,以比较飞行时间和成本。
以上是 图论(graph theory)算法原理、实现和应用全解 的全部内容, 来源链接: utcz.com/p/203603.html