不相交集（disjoint set）原理和实现图文详解

  • Z时代
  • 2024-01-10
  • 分类：IT

不相交集（disjoint

set）是一种数据结构，又称为并查集（union-find set），或称为联合-查找数据结构或合并查找数据结构，该数据结构主要是使用联合-查找算法（union-find algorithm）。不相交集是一种很有用的数据结构，算法简单而高效，不相交集的应用主要体现在图（graph）中，在图中进行环检测（cycle detection），例如在Kruskal最小生成树算法中，另外也可以解决一些实际问题，例如工作序列最大利润问题。本节不相交集的内容主要还是为了下一节图（graph）数据结构作准备，它也可以独立实现一些功能。

不相交集(disjoint-set)ADT

一、不相交集的等价定义

不相交集也就是互相交集为空的集合，不相交集是一种处理关系的数据结构，特别地，这里使用元素和集合定义等价关系。存在集合S，元素x和y属于S：

  1. 在集合S上存在关系R（Relation）；
  2. XRy等于true或false；
  3. 如果xRy等于true，则说x和y有关系。

等价关系比关系R稍微严格，需要满足以下性质：

  1. 自反性，所有属于S的x，xRx，也就是x和自己有关系；
  2. 对称性，xRy，当且仅当yRx，也就是x和y互相有关系；
  3. 传递性，如果xRy且yRz，则xRz，也就是x和z间接有关系。

这里说的关系是很广泛的，可以是任何关系，集合其实就是数据元素的集合，R是数据元素之间的关系。例如R为关系<=的时候不是等价关系，此时元素为一般实数，缺少对称性，a<=b时不一定b<=a。电气连通性是等价关系，元素为电气设备，一个国家的所有城市也有等价关系，元素为每个城市。

等价关系的问题是，给定一个等价关系~，对于任意的x和y，是否x~y（也就是问x和y是否有等价关系）。解决此问题的一个较好的方式是，先找出属于S的元素x的等价类Q，Q是S的一个子集，该子集包含所有与x有关系的元素，当我们要确定是否x~y时，转换为验证x和y是否在同一个等价类Q中，也就是x和y是否在同一个集合中。

我们可以使用散列方式描述集合中的元素，即Si={i}，0 <= i <= n-1，初始化的时候需要创建n个集合，此时Si和Sj相交为空集，也就是不相交集。

不相交集的基本操作为make-set创建集合、find查找和union合并，下面会介绍不相交集使用路径压缩和按秩合并的优化方式，使用该方式每个操作的平均时间为O(a(n))，a(n)是阿克曼函数的反函数，a(n)在n很大的时候还是小于5，因此算法非常高效。

二、不相交集的应用：图（graph）中的环检测

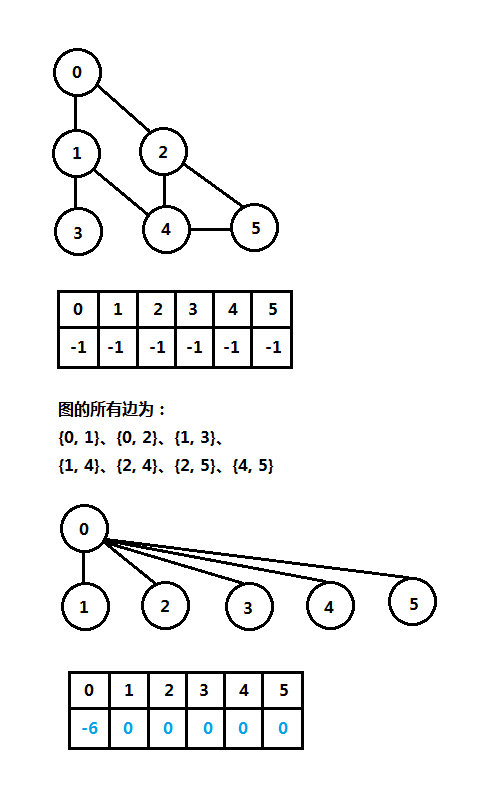
使用并查集(disjoint set)检测图(graph)是否存在环(cycle)

上图中第一个是一个图（graph），每个结点称为顶点（vertices），结点间的连线称为边（edge），现在的问题是在该图中检测环（闭环）。上图中将图中的结点简单地进行0~5标记，两个顶点组成一条边进行检测。如果有两个顶点（一条边）在同一个集合中，则存在一个环；如果两个顶点（一条边）不在一个集合中，则调用合并操作。

这里的关系R为顶点的连接，因此连接的两个顶点组成一个关系。这里仅仅简单结合图说一下不相交集的应用，下面会有相关的实现。

三、不相交集的实现方式和数据结构

不相交集的实现方式有两种，一种是链表，如下图是一个以1为代表的集合：

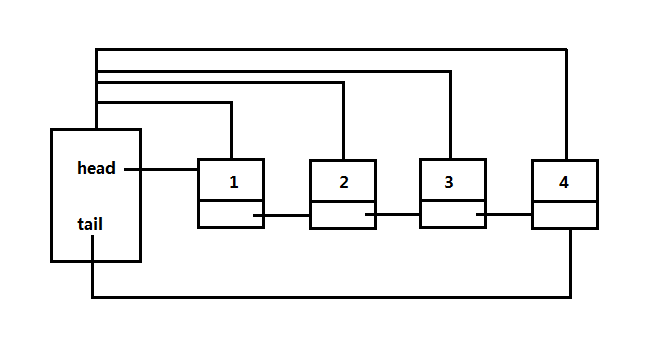
使用链表表示不相交集

使用链表时，链表中的每个元素表示一个集合成员，包含head和tail指针，head指针指向集合的一个元素（该元素称为一个集合的代表元素），一个指向下一个元素的指针，一个指向集合对象自身的指针，这里重点是谈下面的树的实现方式。

另一种方式是使用多路有根树，也叫并查集森林，这时候选取根元素作为集合的代表，每个结点保存父结点，根结点的父元素为自身，表示自身可以使用-1或0，如下图是一个以1为代表的集合：

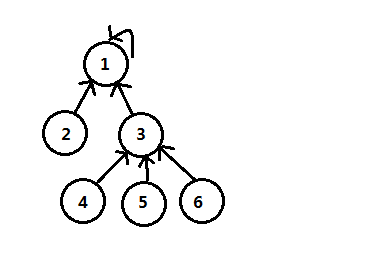
使用有根树表示集合

由上面我们可以看到，对于集合中的数据元素我们是不需要显式表示的，只需要给结点元素做记号即可，也就是使用散列的方式描述元素，使用一个连续的数字序列即可。对于父结点，同样可使用数字序列，根结点的父结点为-1或0。

四、算法操作

这里是使用有根树的实现方式实现不相交集，对于优化的地方就不再一步步循序渐进地讲解，因为是树的原因，在合并的时候可以按照大小合并和按秩合并（按树高度），按大小合并也就是按照树的结点数量，总是将更小的树连接到更大的树上，按秩合并是将浅的树连接成为深的树的子树，这两种方式都是为了降低树的高度，这里实现使用的是按秩合并。

另外在合并操作的进一步优化则是路径压缩，它的意思是，尽量将结点的父结点指向根结点，这样查找起来更快速，下图是一个集合，以及该集合使用数组表示的形式，这里有两个数组parent和rank（单元素时集合的大小），中间current是数组的索引：

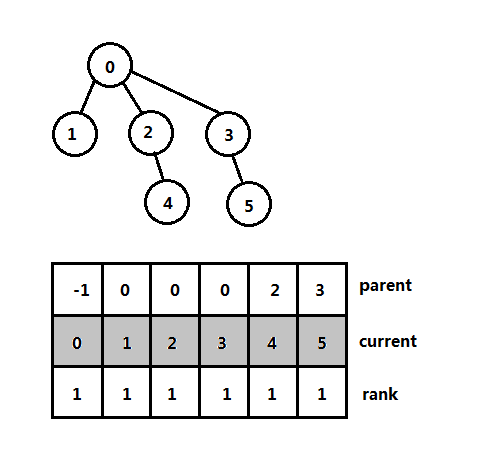
不相交集树和数组表示实例

以上是使用一个数组表示一个树，使用数组的索引为集合元素的记号，数组元素值为父结点的记号，下面是不相交集ADT的头文件声明代码：

// 不相交集ADT对外接口
typedef struct disjset{
    int *parent;
    int *rank;
    int n;
} DisjSet;
// 不相交集函数声明
extern DisjSet *disjset_new(int n);
extern void disjset_make_set(DisjSet *disjset, int n);
extern int disjset_find(DisjSet *disjset, int x); // root
extern int disjset_union(DisjSet *disjset, int x, int y); // 0: cycle, 1: union
extern int disjset_clear(DisjSet *disjset);
extern void disjset_cycle_detect(int array[][2], int n, int size);

1、创建集合make-set

首先我们需要创建n个单元素集合，每个元素的父元素为自身，代码如下：

DisjSet *disjset_new(int n){
    if(n < 1){
        perror("n is too small");
        return NULL;
    }
    DisjSet *disjset = (DisjSet*)malloc(sizeof(DisjSet));
    if(!disjset){
        perror("alloc memory for disjset error");
        return NULL;
    }
    disjset->n = n;
    disjset->parent = (int*)malloc(n * sizeof(int));
    if(!disjset->parent){
        perror("alloc memory for parent error");
        free(disjset);
        return NULL;
    }
    disjset_make_set(disjset, n);
    disjset->rank = (int*)malloc(n * sizeof(int));
    if(!disjset->rank){
        perror("alloc memory for rank error");
        free(disjset->parent);
        free(disjset);
        return NULL;
    }
    for (int j = 0; j < n; ++j)
        disjset->rank[j] = 0;
    return disjset;
}
void disjset_make_set(DisjSet *disjset, int n){
    if(disjset == NULL){
        perror("disjset null");
        return;
    }
    for (int i = 0; i < n; ++i)
        disjset->parent[i] = i;
}

2、查找find

该函数可以检查一个元素是否属于一个集合，也可以确定一条边（两个点）是否属于同一集合，返回之后为集合的代表（根），也就是一个集合，即等价类，路径压缩在这里实现，代码如下：

int disjset_find(DisjSet *disjset, int x){
    if(disjset == NULL){
        perror("disjset null");
        return 0;
    }
    // 压缩路径
    if(disjset->parent[x] != x)
        disjset->parent[x] = disjset_find(disjset, disjset->parent[x]);
    return disjset->parent[x];
}

3、联合union

该联合操作先调用find查找检查x、y是否在同一个等价类中，不在同一个等价类则执行合并操作，联合或合并两个集合成一个集合，该操作可以检查一个图是否存在环，合并优化采用按秩合并，这这里实现，代码如下：

int disjset_union(DisjSet *disjset, int x, int y){
    if(disjset == NULL){
        perror("disjset null");
        return 0;
    }
    int x_root = disjset_find(disjset, x);
    int y_root = disjset_find(disjset, y);
    if(x_root == y_root)
        return 0;
    // 按秩合并
    if(disjset->rank[x_root] > disjset->rank[y_root])
        disjset->parent[y_root] = x_root;
    else if(disjset->rank[x_root] < disjset->rank[y_root])
        disjset->parent[x_root] = y_root;
    else{
        disjset->parent[x_root] = y_root;
        disjset->rank[y_root] = disjset->rank[x_root] + 1;
    }
    return 1;
}

不相交集实现的算法相对比较简单，主要是不要忘记了优化的操作，如果没有进行按秩合并和路径压缩，那么树的高度可能会过高，当n越大，那么查找的速度也慢，以上项目完整源码可查看：https://github.com/onnple/disjset。

五、不相交集的应用

1、图（graph）的环检测（cycle detection）

这是不相交集的主要应用，find查找操作确定特定元素在哪个子集中，这可以用来确定两个元素是否在同一个子集中，union联合操作将两个子集连接成一个子集，联合-查找算法可用于检查无向图是否包含环。

2、Kruskal最小生成树算法

在该算法中，同样是使用了不相交集的环检测算法。

3、工作序列最大利润问题

给定一组n个工作任务，其中每个工作任务i都有一个截止日期di >=1和利润>=0。一次只能安排一项工作。每项工作需要一个单位的时间来完成，当且仅当工作在最后期限前完成时，我们才能获利，任务目的是找到利润最大化的工作的子集，该问题可以借助不相交集进行解决。

以上是 不相交集（disjoint set）原理和实现图文详解 的全部内容， 来源链接： utcz.com/p/203602.html

回到顶部