优先队列(priority queue)和堆(heap)详解:二叉堆、d-堆、左式堆、斜堆和二项堆
优先队列(priority
queue)类似于一般队列(queue),一般队列是一种简单的数据结构,特点是先进先出,详情可查看队列数据结构和实例详解。数据结构从最简单的线性结构,到树结构(二叉树、AVL平衡二叉树、伸展树、B-树和B+树原理),然后是上一节谈到的散列表实现原理,本节讨论的优先队列和堆(heap)相对而言常用于辅助实现其它算法,例如数据压缩赫夫曼编码算法、Dijkstra最短路径算法、Prim最短生成树算法,优先队列还可以实现事件模拟、选择问题,另外人工智能中的A*搜索算法和操作系统的线程调度也使用优先队列。
优先队列的特点是元素正常入队,按照优先级的大小进行出队。堆是另一种与优先队列不同的数据结构,一般来说,堆是用来实现优先队列的,非严格来说,优先队列可以等同于堆,因为堆是用来实现优先队列的,所以优先队列的大部分内容都是在讨论堆,但不要忘记主要内容还是优先队列。下面会首先介绍优先队列的定义,然后讨论各中堆的原理和实现。
一、优先队列的概念和定义
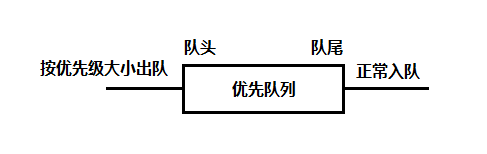
优先队列和普通队列不同的地方在于,在优先队列中,每个记录保存一个优先级值或关键字(本文使用关键字表示),任意记录正常从队尾入队,按照优先级大小或关键字的大小进行出队。最大关键字先出队,称为最大优先队列或降序优先队列;最小关键字先出队,称为最小优先队列或升序优先队列,如下图是一个使用普通数组表示的最大优先队列:
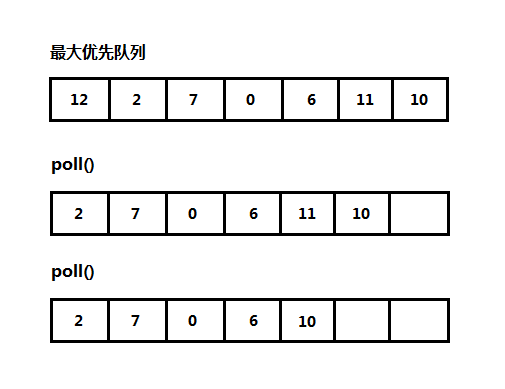
第一次出队操作,关键字12最大,所以12先出队,第二次进行出队操作,此时11最大,所以11出队,如果遇到关键字相等的情况,则按照它们在队中的位置进行出队。
优先队列的实现方式有哪些呢?一般来说,实现优先队列的方式有:有序表或无序表(即数组,或顺序表和链表)、二叉树、AVL平衡二叉树、堆和二叉堆。使用普通的表实现优先队列的性能比较低,有序表插入为O(1),无序表取出为O(n),另外使用普通二叉树实现优先队列只能保证平均时间为O(log n),但最差情况是O(n),AVL树则需要复杂的无关操作,而堆可以实现性能较好的优先队列,取出效率可达到O(1),一般的操作都能达到O(log n)。
二、堆和二叉堆(binary heap)
堆主要用来实现优先队列,二叉堆是堆的一种。堆是一个完全二叉树,也就是一棵二叉树,在叶子上从左到右被完全填满元素,结点中至少包括优先级值或关键字,堆的主要特点是:任意结点的关键字大于或等于(小于或等于)儿子结点,又可分为最大堆(max heap),结点的关键字大于或等于儿子结点;最小堆(min),其结点关键字小于或等于儿子结点,这个特点又称为堆的有序性,下图是最大堆的一个实例:
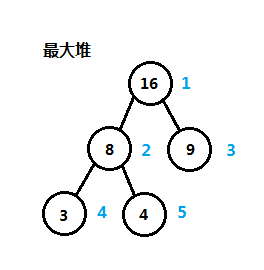
1、二叉堆的概念和定义
上图就是一个二叉堆,二叉堆是堆的最简单形式,设二叉堆的高度为h,二叉堆的所有叶子结点位于第h层或第h-1层(h>0),高度为h的二叉堆有2^h到2^(h+1)-1个结点,其中h=log n。堆的实现方式可使用顺序表或数组和二叉树,不管哪种实现方式,优先队列或堆的表示一般都是使用二叉树或多叉树。看下图中的二叉堆和对应的数组,根据它们的索引,我们看另一种二叉堆的逻辑定义:
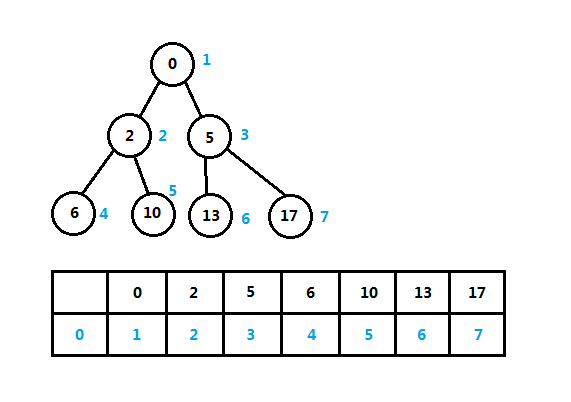
上图是一个最小堆,任意结点关键字小于或等于儿子结点,给堆中的结点从左到右加上索引,对应于数组中的索引和关键字。这是二叉堆使用数组表示的一种常见形式,得出二叉堆的逻辑定义如下:
- n个元素序列{k1, k2, …, ki, …, kn},k为关键字或优先级值,i为元素的索引;
- 任取i属于{1, 2, 3, …, n/2};
- 最小堆表示为:ki <= k2i,ki <= k(2i+1);
- 最大堆表示为:ki >= k2i,ki >= k(2i+1)。
以上定义从1开始,也可以从0开始,两者的区别是,使用0开始需要对0进行检测,若使用1开始,最大堆第0个放一个极大的值,最小堆放一个极小的值,因为使用数组表示二叉堆,所以堆的大小需要预先进行预测。下面索引从第0个开始,结点间的索引关系为:
- i为第i个结点,根结点没有父结点;
- 父结点索引为:(i-1)/2;
- 左结点索引为:2*i+1;
- 右结点索引为:2*i+2。
2、二叉堆的基本操作详细实现
下面讨论的二叉堆操作是优先队列的基本操作,其它堆实现时也是提供类似的操作,其中最重要的两个操作就是入队和出队,入队又称为插入操作,出队又称为删除最小/最大元素,下面是常见的优先队列操作,首先看看下面,最小二叉堆的ADT声明:
// 使用最小二叉堆使用优先队列// 基本数据记录
typedef struct Song{
char name[128];
char singer[128];
} Song;
// 结点
typedef struct qnode{
int key; // 关键字或优先级值
Song song;
} QNode;
// 优先队列对外ADT
typedef struct priorityqueue{
int length; // 数组长度
int size; // 记录数量
QNode **list; // 记录数组,使用一个数组表示一个二叉堆/二叉树
} PriorityQueue;
// 最小堆优先队列函数声明
extern PriorityQueue *pqueue_init(int length);
extern int pqueue_is_empty(PriorityQueue *queue);
extern int pqueue_is_full(PriorityQueue *queue);
extern int pqueue_push(PriorityQueue *queue, int key, Song *song);
extern QNode *pqueue_top(PriorityQueue *queue); // 获取顶部元素
extern int pqueue_pop(PriorityQueue *queue); // 释放顶部元素
extern int pqueue_decrease(PriorityQueue *queue, int index, int delta);
extern int pqueue_increase(PriorityQueue *queue, int index, int delta);
extern int pqueue_delete(PriorityQueue *queue, int index);
extern PriorityQueue *pqueue_build(QNode *list, int length);
extern void pqueue_traverse(PriorityQueue *queue);
extern int pqueue_clear(PriorityQueue *queue);
该最小二叉堆优先队列的实现提供了完整的操作,包括检查优先队列是否已满、入队或插入操作、删除或出队操作、增加和降低关键字的值、删除关键字和直接构建优先队列的操作。
(1)二叉堆插入和上滤操作图解
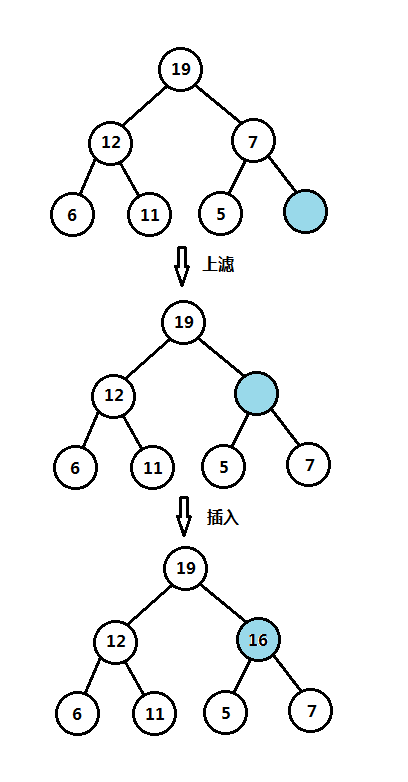
(2)二叉堆删除和下滤操作图解
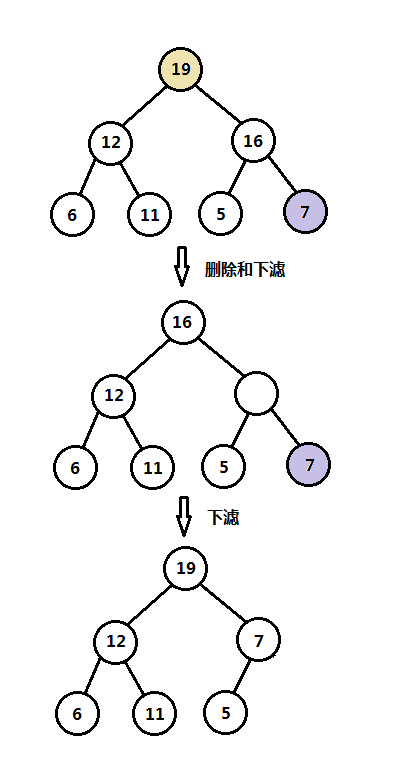
注意,以上是使用一个数组来表示一个二叉树,虽然是使用数组表示,但是操作方式依然是按照二叉树的形式操作,后面还可能会有类似的表示方式,以上最小二叉堆优先队列完整实现可在github上查看,在main.c文件中提供类似STL库的使用方式:https://github.com/onnple/priorityqueue。
三、d-堆(d-heap)
d-堆是二叉堆的推广,d-堆的每个结点有d个儿子,二叉堆也就是2-堆,又类似于树中的B树或散列表中的可扩散列表。d-堆的所有基本操作时间复杂度为O(log n),底数为d,删除/出队操作时间复杂度为O(d log n),底数为d,下面是一个3-堆的实例:
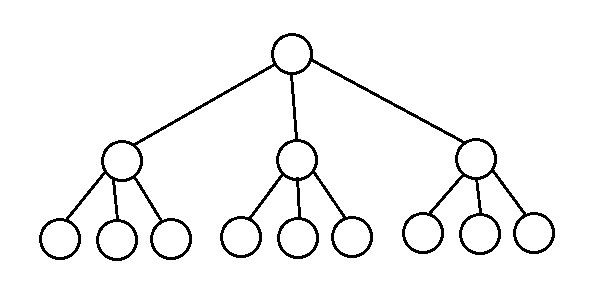
当优先队列过大而不适合放在内存中时,可采取类似B树的方式操作d-堆。在讨论堆中有一个基本的操作:合并(merge),d-堆的合并操作比较困难,下面介绍的三种堆(左式堆、斜堆和二项堆)都支持高效率的合并。
四、左式堆(leftist heap)
1、左式堆的定义
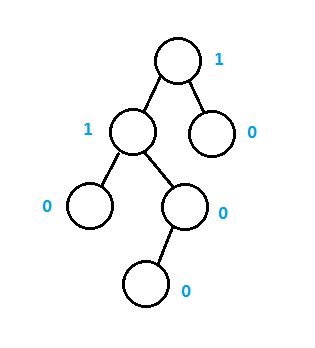
左式堆是一种支持合并的堆,合并是集合的基本操作,在第一节有谈到集合这种数据结构,其特点是数据结构之间没有任何关系,和数学中的集合是类似的。所有支持高效合并的数据结构都需要使用指针,但是可能会导致其它操作变慢。
如上图是一个左式堆的例子,类似于AVL平衡二叉树,提供相关的平衡信息,和二叉堆一样具有相同的堆序性,同样也是二叉树的形式,左式堆的所有操作都是以合并为主,删除和插入都是使用合并,合并操作的时间复杂度为O(log n)。
左式堆的平衡信息使用结点的零路径长,零路径长是指结点到一个没有两个儿子的叶子结点的最短路径长,空结点的最短路径长为-1,零路径长实际是结点的最短高度,也就是到最近树叶的距离,如上图的蓝色数字是对应结点的零路径长。
2、左式堆的性质
(1)堆序性,一般左式堆都是使用最小堆(也可以实现最大堆),对于最小堆,任意结点关键字大于或等于其父结点的关键字,也就是key(i) >= key(parent(i))。
(2)左边树更深,任意结点的左儿子零路径长大于或等于右儿子零路径长,也就是distance(left(i)) >= distance(right(i));任意结点的零路径长比右儿子的零路径长最小值多1,也就是distance(i)=1+distance(right(i))。
在右路径上有r个结点的左式树必然至少有2^r-1个结点,函数n个结点的左式树,其右路径最多有log(n+1)个结点,因此将左式堆的所有操作放在右路径上进行会更加节省时间,相关操作可能需要相应的恢复性质的操作。
3、左式堆的数据结构
左式堆的实现不使用数组表示,而是使用二叉树表示,其数据结构成员至少包括:
- 数据项,实体数据;
- 关键字或优先级值;
- 左右儿子,和二叉树的一样;
- 零路径长,和AVL树的结点高度一样。
4、左式堆的合并操作
左式堆的所有基本操作都可以使用合并操作,插入是合并的特殊情况,即合并操作已经包括插入操作,插入可看作是一个单结点堆和一个大的堆的合并。
合并的核心主要是将两个堆的右路径上的结点进行合并(这里使用最小堆),每次递归合并处理,更新已合并根结点的零路径长,检查根结点左右儿子是否符合左式堆属性。
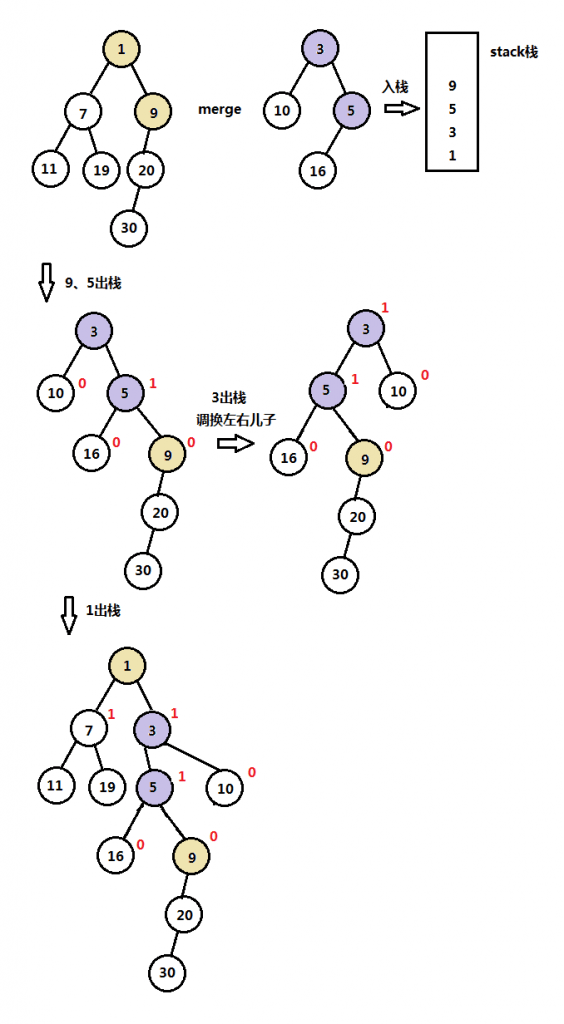
h1和h2是两个最小左式堆,若h1和h2中有一个空堆,则返回非空堆,如果两个都不是空堆,则进行合并操作,下面是详细的合并步骤:
- 比较h1和h2根关键字大小,如key(root(h1))
> key(root(h2));
- 将最小的关键字结点入栈,在最小关键字的堆中位置移动到下一个最右边的儿子(下移操作);
- 递归比较两个堆的关键字,将最小关键字结点入栈,并在最小关键字的堆中下移到下一个右儿子;
- 重复操作,知道遇到一个null结点;
- 将最后处理的结点作为栈顶的右儿子,并调整该子树转为左式堆;
- 递归将栈元素出栈,将出栈的元素作为栈顶的右儿子,并调整为左式堆。
下图是两个左式堆合并的完整实例图解:
5、左式堆完整代码实现
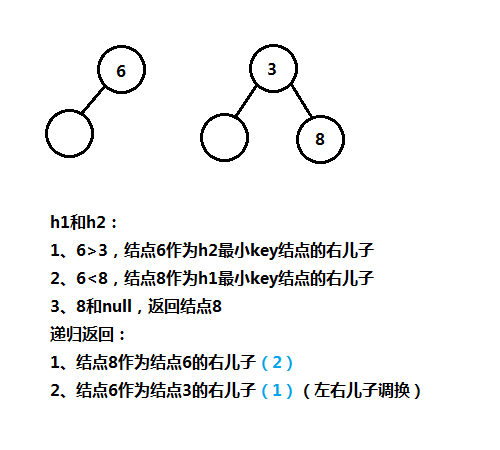
上面解释的合并步骤是以栈为基础的,可以使用栈作为辅助,也可以不使用栈辅助仅是作为一种逻辑处理方式,我们可以使用递归的方式进行处理,上图是递归处理的实例图解,下面是左式堆的ADT声明:
// 左式堆实现优先队列(最小堆)// 实体数据
typedef struct label{
int color;
char title[128];
} Label;
// 左式堆结点
typedef struct lnode{
int key;
int dist;
Label label;
struct lnode *left;
struct lnode *right;
} LNode;
// 左式堆对外ADT
typedef struct leftistheap{
int size;
LNode *root;
} LeftistHeap;
// 左式堆操作函数声明(参考优先队列的基本操作)
extern LeftistHeap *lheap_init();
extern int lheap_is_full(LeftistHeap *heap);
extern int lheap_is_empty(LeftistHeap *heap);
extern int lheap_push(LeftistHeap *heap, int key, Label *label);
extern LNode *lheap_top(LeftistHeap *heap);
extern int lheap_pop(LeftistHeap *heap);
extern void lheap_traverse(LeftistHeap *heap);
extern int lheap_clear(LeftistHeap *heap);
以上左式堆的实现相对比较简单,主要是合并操作,使用栈也会比较简单,其完整源码可在github上查看:https://github.com/onnple/leftistheap,其中调用例子中的左式堆如下:
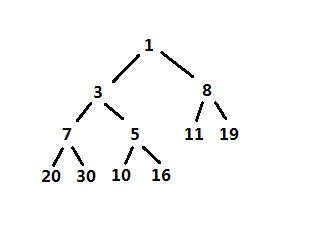
五、斜堆(skew heap)
斜堆类似于伸展树,也就是对左式堆的扩展,不需要相关的平衡信息,只需要保留堆的基本有序性,和上面使用数组表示的二叉堆对比,斜堆则是使用二叉树表示的。斜堆的最坏执行情况为O(n)(链表的形式),每次操作的摊还时间为O(log n),斜堆的基本操作也是合并。
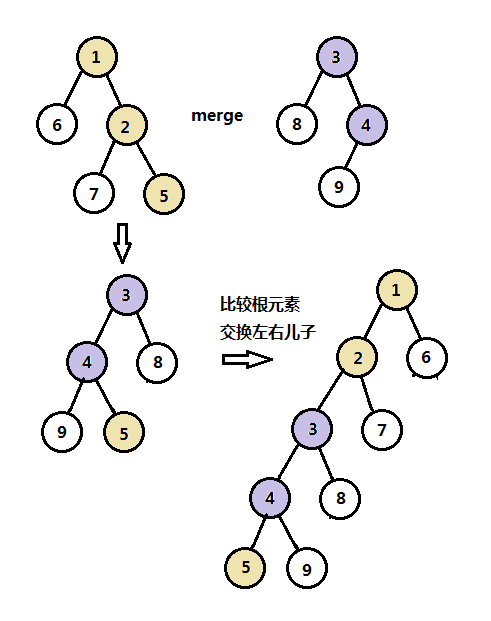
1、斜堆合并操作
斜堆的基本操作和左式堆一样,主要对右路径的结点进行合并,其中有两个例外的地方,如下:
- 左式堆需要检查左右儿子是否满足左式堆的性质,斜堆则不需要;
- 斜堆除了最大关键字结点外,其它结点都无条件交换左右儿子。
下图是斜堆合并操作的完整图解:
2、斜堆代码实现
和左式堆的实现类似,可借用栈或直接处理,另外要注意上面提到的两点,下面是斜堆的ADT声明:
// 斜堆实现优先队列// 数据实体
typedef struct process{
int threads;
int memsize;
} Process;
// 斜堆结点
typedef struct knode{
int key;
Process process;
struct knode *left;
struct knode *right;
} KNode;
// 斜堆对外ADT
typedef struct skewheap{
int size;
KNode *root;
} SkewHeap;
// 斜堆实现优先队列,函数操作声明
extern SkewHeap *sheap_init();
extern int sheap_is_full(SkewHeap *heap);
extern int sheap_is_empty(SkewHeap *heap);
extern int sheap_push(SkewHeap *heap, int key, Process *process);
extern KNode *sheap_top(SkewHeap *heap);
extern int sheap_pop(SkewHeap *heap);
extern void sheap_traverse(SkewHeap *heap);
extern int sheap_clear(SkewHeap *heap);
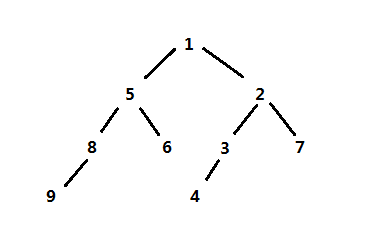
斜堆的实现和左式堆的实现差不多,同样可以使用栈作为辅助,完整实现源码可查看github项目:https://github.com/onnple/skewheap,项目调用实例其中的堆为:
六、二项队列(binomial queue)
二项队列使用二项堆(binomial
heap)实现,二项堆的主要应用是实现优先队列,而二项堆是二项树的合集,也就是多个二项树形式一个二项堆,又称为森林。
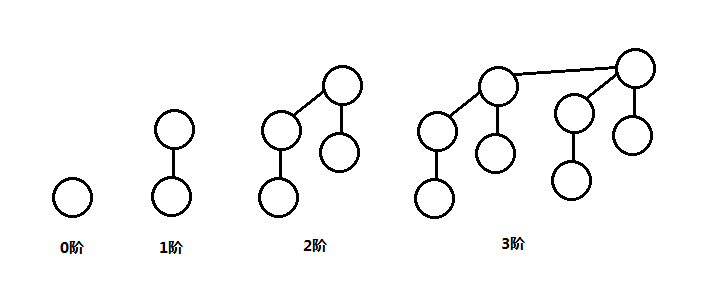
0阶二项树有1个结点,k阶二项树由两个k-1阶的二项树组成,其中一个二项树作为另一个的最左儿子(也可以放在最右边),k阶二项树的特点如下:
- k阶二项树有2^k个结点;
- 深度为k;
- 深度i处有kCi个结点,0 <= i <=k;
- 根结点的度数为k,从右到左的子树阶数k-1, k-2, …, 0。
一个二项堆中的二项树的数量等于二项堆结点数量n的二进制表示中的1的个数,或为O(log
n),下面是一个二项堆的实例:
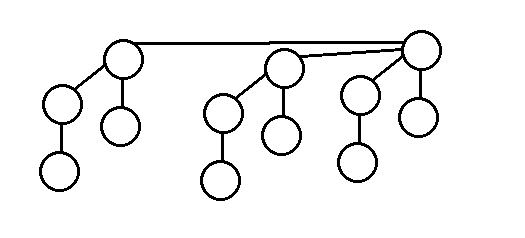
以上二项堆的元素个数为n=12,二进制表示为1100,也就是有2棵二项树,分别是2阶二项树和3阶二项树组成,log(12)向上取整也为3,二项堆的最坏运行时间为O(log n)。
1、二项堆的数据结构
二项堆的表示形式同样使用类似二叉树的形式,基本数据结构是类似的,但有些地方稍有不同,后面会有提到。
- 关键字和数据项;
- 度数;
- 最左儿子;
- 其它儿子(兄弟)数组;
- 父结点。
2、二项堆的基本操作
(1)合并操作
二项堆的所有主要操作都依赖于合并操作,h1和h2是两个二项堆,如果其中有一个为空堆则返回另一个堆。
合并的第一个操作是直接合并:找出h1和h2的多个二项树,按照二项树的度数或阶数从左到右升序的方式预先合并两个二项堆。
接着对已合并的树进行调整,以确保满足二项堆的性质:
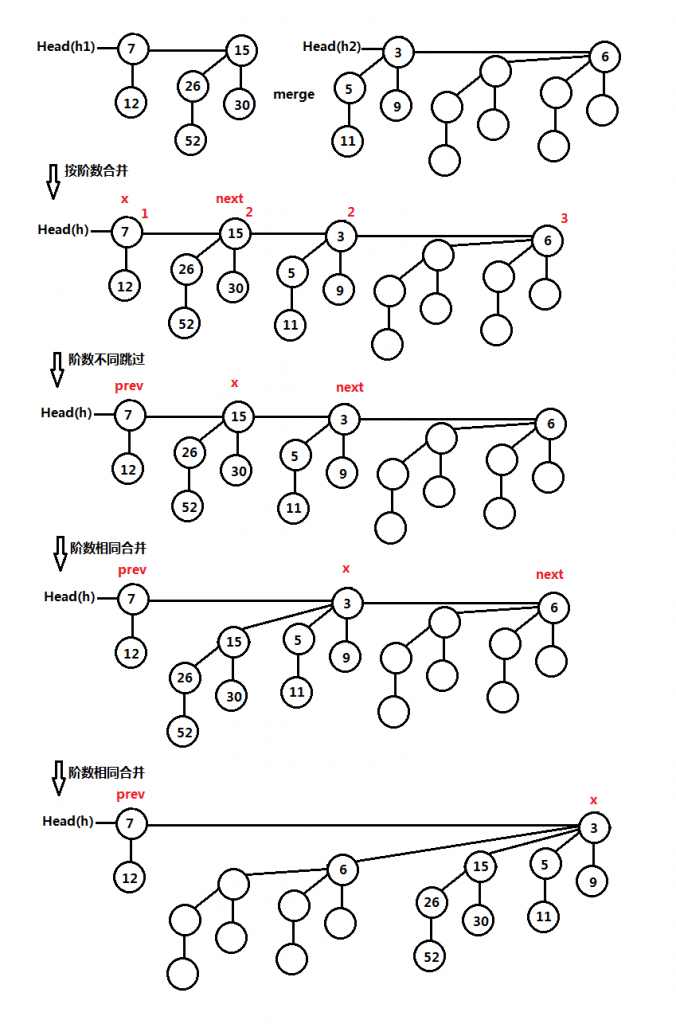
- 最多只有一个二项树是任意阶数,也就是说,在一个二项堆中每个二项树的阶数都不一样,若遇到相同阶数的二项树则合并,这是调整的最主要原则。合并操作从左到右遍历已合并的各个二项树根结点。
- 遍历已合并的二项树根结点,从最左边的结点开始遍历,当前结点为x,上一个结点为prev,下一个结点为next,下一个的下一个为next-next。
- x和next的阶数不同,跳过不处理。
- x和next的阶数相同。(1)x和next-next的阶数相同,跳过处理;(2)x的关键字小于或等于next,将next作为x的最左儿子;(3)x的关键字大于next,将x作为next的最左儿子。
下图是二项堆合并操作的完整实例图解:
(2)最小元
寻找最小元可通过搜索所有二项树的根找出,也就是从根结点的最左元素开始,时间为O(log n),一个二项堆中最多有O(log n)棵不同的树,另外或者也可以在其它操作中将最小元放到根上,即可达到O(1)。
(3)删除最小元
先找出拥有最小元的二项树C的根,除了树根外,使用该树C的其它元素创建一棵新的二项堆A,除了拥有最小元的二项树C外,其它二项树重新组成一个新的二项堆B,将这两个二项堆A和B进行合并即可完成删除操作。
3、二项队列或二项堆的实现代码
在本实现中,根结点不指向所有儿子结点,只指向最左儿子,由这个儿子的兄弟指针指向其它儿子;另外所有二项树的根结点均用一个表存起来,这里使用链表,额外实现了一个双向循环链表(如果你用其它语言实现,则可以使用类似list的容器)。代码稍微有些复杂,下面先看二项堆ADT的声明代码:
#include "list.h"// 二项堆实现优先队列BinomialHeap
// 数据项
typedef struct area{
int width;
int height;
} Area;
// 结点
typedef struct anode{
int key;
Area value;
int degree;
struct anode *parent, *sibling, *child;
} ANode;
// 二项堆对外ADT
typedef struct binomialheap{
list *list;
int size;
} BinomialHeap;
// 二项堆优先队列操作函数声明
extern BinomialHeap *bheap_init();
extern int bheap_is_full(BinomialHeap *bheap);
extern int bheap_is_empty(BinomialHeap *bheap);
extern int bheap_push(BinomialHeap *bheap, int key, Area *value);
extern ANode *bheap_top(BinomialHeap *bheap);
extern void bheap_pop(BinomialHeap *bheap);
extern void bheap_traverse(BinomialHeap *bheap);
extern int bheap_clear(BinomialHeap *bheap);
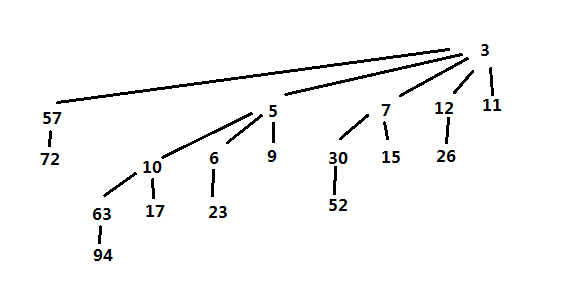
优先队列的操作都是类似的,以上使用二项堆实现的优先队列,完整源码可以在github上的项目查看:https://github.com/onnple/binomialheap。其中在main文件中有调用实例,实例中的二项堆如下图:
七、优先队列和堆的应用
1、编程语言中的实现
C++的STL库中提供优先队列,Boost则提供更完整的优先队列和不同的堆,如二项堆、d-堆、斐波那契堆、配对堆和斜堆等,其它语言如Java、Python、PHP、Perl、Go也有提供。
2、使用优先队列的Dijkstra最短路径算法
当图以邻接表或矩阵的形式存储时,优先队列可以在实现Dijkstra算法时有效地提取最小值。
3、Prim算法
实现Prim算法存储节点密钥,每一步提取最小密钥节点。
4、数据压缩
用于压缩数据的哈夫曼编码中。
5、人工智能中的A*搜索算法
A*搜索算法寻找加权图中两个顶点之间的最短路径,先尝试最有希望的路径。优先级队列(也称为边缘)用于跟踪未探索的路由,总路径长度的下界最小的路由具有最高优先级。
6、堆排序
堆排序通常使用堆实现,堆是优先级队列的实现。
7、操作系统
它也用于操作系统的负载平衡(服务器上的负载平衡)、中断处理。
以上是 优先队列(priority queue)和堆(heap)详解:二叉堆、d-堆、左式堆、斜堆和二项堆 的全部内容, 来源链接: utcz.com/p/203600.html