【React】求2次贝赛尔曲线上任一点的切线的倾斜角度

【React】求2次贝赛尔曲线上任一点的切线的倾斜角度

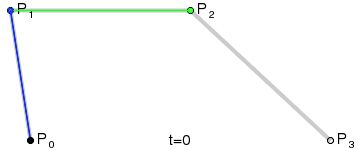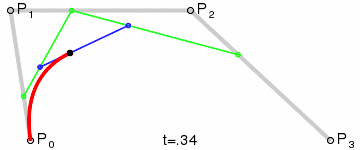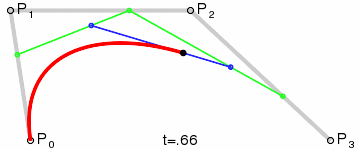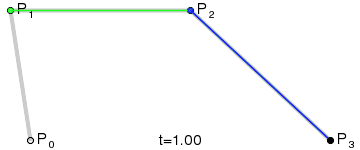
给定x坐标, 想知道这条蓝色线的倾斜角度

现实中需求: 紧贴曲线上画文字, 求个思路

回答

你的图像是三阶贝塞尔曲线

P0 = [0, 0]
P1 = [-1, 10]
P2 = [8, 10]
P3 = [12, 0]
//(1 - t)^3P0 + 3t(1- t)^2P1 + 3t^2(1 - t)P2 + t^3P3化简
//(P3 - 3P2 + 3P1 - P0)t^3 + (3P2 - 6P1 + 3P0)t^2 + (3P1 - 3P0)t + P0
a = P3[0] - 3 * P2[0] + 3 * P1[0] - P0[0]
b = 3 * P2[0] - 6 * P1[0] + 3 * P0[0]
c = 3 * P1[0] - 3 * P0[0]
d = P0[0]
function f(x){
    t = Math_yyz.getCubicRoot(a, b, c, d - x);
    realt = t.find((n) => n >= 0 && n <= 1 && n !== null)
    pm = f1(realt, P0, P1, P2);
    pn = f1(realt, P1, P2, P3);
    return (pm[1] - pn[1]) / (pm[0] - pn[0]);
}
function f1(t, p0, p1, p2){
    return [(1 - t) * (1 - t) * p0[0] + 2 * t * (1 - t) * p1[0] + t * t * p2[0], (1 - t) * (1 - t) * p0[1] + 2 * t * (1 - t) * p1[1] + t * t * p2[1]];
}
f(4)得到x=4的斜率

//求一元三次方程，网上找的
Math_yyz=(function(){ 
var module={}; 
function eqZero(x){ 
return Math.abs(x)<1e-6; 
} 
var abs=Math.abs; 
var pow=Math.pow; 
var sqrt=Math.sqrt; 
var sign=Math.sign; 
var cos=Math.cos; 
var acos=Math.acos; 
var TwoPi=Math.PI*2; 
function getCubicRoot(a,b,c,d){ 
a=a; 
b=b/(3*a); 
c=c/(6*a); 
d=d/(2*a); 
var solve=[null,null,null]; 
var Alph=-b*b*b+3*b*c-d; 
var Beta=b*b-2*c; 
var Delt=Alph*Alph-Beta*Beta*Beta; 
var R1,R2,tht; 
if (eqZero(Delt)){ 
R1=abs(pow(abs(Alph),1/3))*sign(Alph); 
if (eqZero(R1)){ 
solve[0]=-b; 
} 
else{ 
solve[0]=-b+2*R1; 
solve[1]=-b-R1; 
} 
} 
else if(Delt>0){ 
//var tht,R1,R2; 
tht=Alph+sqrt(Delt); 
R1=abs(pow(abs(tht),1/3))*sign(tht); 
tht=Alph-sqrt(Delt); 
R2=abs(pow(abs(tht),1/3))*sign(tht); 
solve[0]=-b+R1+R2; 
} 
else if(Delt<0){ 
//var tht; 
tht=acos(Alph/(sqrt(Beta)*Beta)); 
solve[0]=-b+2*sqrt(Beta)*cos(tht/3); 
solve[1]=-b+2*sqrt(Beta)*cos((tht+TwoPi)/3.0); 
solve[2]=-b+2*sqrt(Beta)*cos((tht-TwoPi)/3); 
} 
return solve; 
} 
module.getCubicRoot=getCubicRoot; 
return module; 
})();

##########
二阶贝塞尔曲线
##########
根据公式：
Pm(t) = (1-t)P0 + tP1
Pn(t) = (1-t)P1 + tP2
B(t) = (1-t)Pm(t) + tPn(t) 
= (1-t)^2 P0 + 2(1-t)tP1+ t^2P2
已知X坐标X0
Bx(t) = (1-t)^2 P0x + 2(1-t)tP1x+ t^2P2x = X0 （一元二次方程）求解出t, 并带入Pm, Pn得到蓝线，求斜率即可，暴力解法

以上是 【React】求2次贝赛尔曲线上任一点的切线的倾斜角度 的全部内容， 来源链接： utcz.com/a/75686.html

回到顶部