动态查找-二叉排序树

Z时代
2024-01-10
分类：技术分享

概念

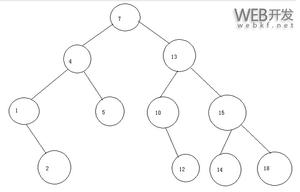
⼆叉排序树(Binary Sort Tree),⼜称为⼆叉查找树. 它或者是⼀颗空树.或者是⼀颗具有下列性质的⼆叉树;
若它的左⼦树不空,则左⼦树上所有结点的值均⼩于它的根结构的值;
若它的右⼦树不空,则右⼦树上的所有结点的值均⼤于它的根结点的值; 它的左右⼦树也分别是⼆叉排序树;

二叉排序树的查找操作

实现思路
从根节点开始比较，如果大于根结点（根据二叉排序树的概念）直接从根节点的右子树开始继续查找，如果小于则从当前结点的左子树继续查找。

实现代码

//1.二叉排序树--查找
/*
递归查找二叉排序树T中,是否存在key;
指针f指向T的双亲,器初始值为NULL;
若查找成功,则指针p指向该数据元素的结点,并且返回TRUE;
若指针p指向查找路径上访问的最后一个结点则返回FALSE;
*/
Status SearchBST(BiTree T,int key,BiTree f, BiTree *p){
//如果根节点都是空则返回错误
if(!T){
//直接返回双亲结点
*p =f;
return FALSE;
}
if(T->data == key){
//当查找的元素就等于根节点 直接返回根节点
(*p) = T;
return TRUE;
}elseif(key > T->data){
//当查找的元素大于根节点的元素（根据二叉排序树的特性）直接去右子树继续查找并传入双亲结点
return SearchBST(T->rchild, key, T, p);
}else{
//当查找的元素小于根节点的元素（根据二叉排序树的特性）直接去坐左树继续查找并传入双亲结点
return SearchBST(T->lchild, key, T, p);
}
return FALSE;
}

二叉排序树的插入操作

实现思路
先查找需要插入元素的值是否已经存在于二叉排序树中如果存在则不进行插入操作，如果不存在按照上述的查找方法会返回查找路径上访问的最后一个结点，开始比较插入元素的值和最后一个结点的大小，更大插入右节点反之插入左节点

实现代码

//2.二叉排序树-插入
/*  当二叉排序树T中不存在关键字等于key的数据元素时， */
/*  插入key并返回TRUE，否则返回FALSE */
Status InsertBST(BiTree *T, int key) {
BiTree p;
if(SearchBST(*T, key, NULL, &p)){
//如果元素已经存在则直接返回插入失败
return FALSE;
}else{
BiTree s = (BiNode *)malloc(sizeof(BiNode));
if(!s) return FALSE;
s->data = key;
s->lchild = s->rchild = NULL;
if(p == NULL){
//说明是空树
*T = s;
}else{
//开始判断当前的值和树的最后一个结点的大小，大插到右边，小插左边
if(p->data > key){
p->lchild = s;
}else{
p->rchild = s;
}
}
return TRUE;
}
}

二叉排序树的删除操作

实现思路
主要分三种情况
1. 删除的结点是叶子结点；这种情况最好处理只要找到对应的结点删除即可
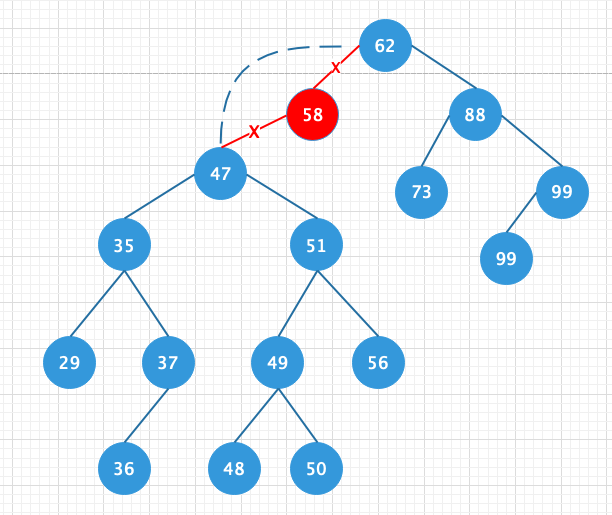
2. 删除的结点非叶子结点但是仅含有左结点或者右结点；这种情况只需要将待删除结点的右结点或者左节点的值和左右结点赋值给待删除的结点就好如图删除的是58这个结点
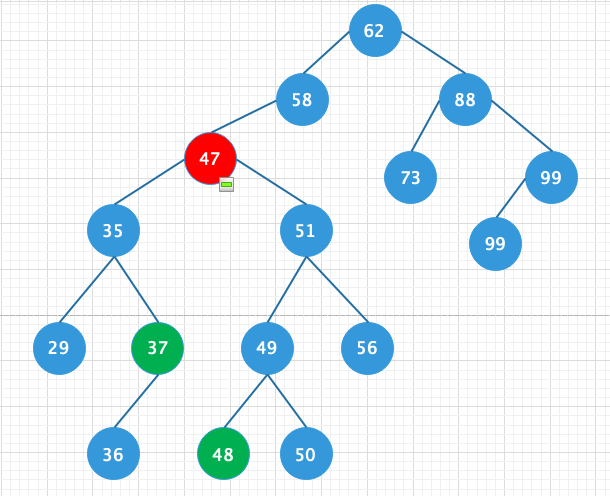
3. 删除的结点既有左结点又含有右结点；这种情况就是找到待删除结点的左节点，然后一直向下寻找左结点的右结点，然后继续右结点的右结点，一直往下找直到右结点为null的结点，则用找到的这个结点替换待删除的结点，或者说找到待删除结点的右结点，然后再找右结点的左节点，一直往下找左节点直到找到左节点为null的结点然后用这个结点替换待删除的结点，在中序遍历中这两个结点分别是待删除结点的前后两个结点，用这两个结点替代待删除的结点对数的改动最小如图删除47这个结点按上述步骤可以找到37结点和48结点可以用这两个结点中的任意一个结点替换待删除位置的结点

实现代码

//3.从二叉排序树中删除结点p,并重接它的左或者右子树;
//f
Status Delete(BiTree *p){
if((*p)->lchild && (*p)->rchild){
//如果删除的结点的左子树和右子树都不为空
//找到左子树的最后一个右结点或者找到右子树最后一个左节点
//（其实中序遍历的话这两个结点刚好是待删除结点的前后两个结点）
//所以用这两个结点替换待删除的结点树的改动最小
//查找左子树的最后一个结点
BiTree temp;
BiTree s = NULL;
temp = (*p)->lchild;
while (temp->rchild) {
s = temp;
temp = temp->rchild;
}
//开始赋值
(*p)->data = temp->data;
if(s){
s->rchild = temp->lchild;
}
free(temp);
}elseif((*p)->lchild){
BiTree temp;
temp = *p;
*p = (*p)->lchild;
free(temp);
}elseif((*p)->rchild){
BiTree temp;
temp = *p;
*p = (*p)->rchild;
free(temp);
}else{
*p = NULL;
free(*p);
}
return TRUE;
}
//4.查找结点,并将其在二叉排序中删除;
/* 若二叉排序树T中存在关键字等于key的数据元素时，则删除该数据元素结点, */
/* 并返回TRUE；否则返回FALSE。 */
Status DeleteBST(BiTree *T,int key){
//不存在关键字等于key的数据元素
if(!*T)
return FALSE;
else
{
//找到关键字等于key的数据元素
if (key==(*T)->data)
return Delete(T);
elseif (key<(*T)->data)
//关键字key小于当前结点,则缩小查找范围到它的左子树;
return DeleteBST(&(*T)->lchild,key);
else
//关键字key大于当前结点,则缩小查找范围到它的右子树;
return DeleteBST(&(*T)->rchild,key);
}
}

完整代码

//
//  main.c
//  二叉排序树
//
//  Created by xzkj on 2020/6/3.
//  Copyright © 2020 TuDou. All rights reserved.
//
#include <stdio.h>
#include "stdlib.h"
#define FALSE 0
#define TRUE 1
typedef int Status;
typedef struct BiNode{
int data; //数据
struct BiNode *lchild,*rchild; //左孩子和右孩子
}BiNode,*BiTree;
//1.二叉排序树--查找
/*
递归查找二叉排序树T中,是否存在key;
指针f指向T的双亲,器初始值为NULL;
若查找成功,则指针p指向该数据元素的结点,并且返回TRUE;
若指针p指向查找路径上访问的最后一个结点则返回FALSE;
*/
Status SearchBST(BiTree T,int key,BiTree f, BiTree *p){
//如果根节点都是空则返回错误
if(!T){
//直接返回双亲结点
*p =f;
return FALSE;
}
if(T->data == key){
//当查找的元素就等于根节点 直接返回根节点
(*p) = T;
return TRUE;
}elseif(key > T->data){
//当查找的元素大于根节点的元素（根据二叉排序树的特性）直接去右子树继续查找并传入双亲结点
return SearchBST(T->rchild, key, T, p);
}else{
//当查找的元素小于根节点的元素（根据二叉排序树的特性）直接去坐左树继续查找并传入双亲结点
return SearchBST(T->lchild, key, T, p);
}
return FALSE;
}
//2.二叉排序树-插入
/*  当二叉排序树T中不存在关键字等于key的数据元素时， */
/*  插入key并返回TRUE，否则返回FALSE */
Status InsertBST(BiTree *T, int key) {
BiTree p;
if(SearchBST(*T, key, NULL, &p)){
//如果元素已经存在则直接返回插入失败
return FALSE;
}else{
BiTree s = (BiNode *)malloc(sizeof(BiNode));
if(!s) return FALSE;
s->data = key;
s->lchild = s->rchild = NULL;
if(p == NULL){
//说明是空树
*T = s;
}else{
//开始判断当前的值和树的最后一个结点的大小，大插到右边，小插左边
if(p->data > key){
p->lchild = s;
}else{
p->rchild = s;
}
}
return TRUE;
}
}
//3.从二叉排序树中删除结点p,并重接它的左或者右子树;
//f
Status Delete(BiTree *p){
if((*p)->lchild && (*p)->rchild){
//如果删除的结点的左子树和右子树都不为空
//找到左子树的最后一个右结点或者找到右子树最后一个左节点
//（其实中序遍历的话这两个结点刚好是待删除结点的前后两个结点）
//所以用这两个结点替换待删除的结点树的改动最小
//查找左子树的最后一个结点
BiTree temp;
BiTree s = NULL;
temp = (*p)->lchild;
while (temp->rchild) {
s = temp;
temp = temp->rchild;
}
//开始赋值
(*p)->data = temp->data;
if(s){
s->rchild = temp->lchild;
}
free(temp);
}elseif((*p)->lchild){
BiTree temp;
temp = *p;
*p = (*p)->lchild;
free(temp);
}elseif((*p)->rchild){
BiTree temp;
temp = *p;
*p = (*p)->rchild;
free(temp);
}else{
*p = NULL;
free(*p);
}
return TRUE;
}
//4.查找结点,并将其在二叉排序中删除;
/* 若二叉排序树T中存在关键字等于key的数据元素时，则删除该数据元素结点, */
/* 并返回TRUE；否则返回FALSE。 */
Status DeleteBST(BiTree *T,int key){
//不存在关键字等于key的数据元素
if(!*T)
return FALSE;
else
{
//找到关键字等于key的数据元素
if (key==(*T)->data)
return Delete(T);
elseif (key<(*T)->data)
//关键字key小于当前结点,则缩小查找范围到它的左子树;
return DeleteBST(&(*T)->lchild,key);
else
//关键字key大于当前结点,则缩小查找范围到它的右子树;
return DeleteBST(&(*T)->rchild,key);
}
}
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, World!n");
int i;
int a[10]={62,88,58,47,35,73,51,99,37,93};
BiTree T=NULL;
for(i=0;i<10;i++)
{
InsertBST(&T, a[i]);
}
BiTree p;
int statusValue = SearchBST(T, 99, NULL, &p);
printf("查找%d是否成功:%d (1->YES/0->NO)n",p->data,statusValue);
statusValue = DeleteBST(&T,93);
printf("二叉排序树删除93是否成功:%d (1->YES/0->NO)n",statusValue);
statusValue = DeleteBST(&T,47);
printf("二叉排序树删除47是否成功:%d (1->YES/0->NO)n",statusValue);
statusValue = DeleteBST(&T,12);
printf("二叉排序树删除12是否成功:%d (1->YES/0->NO)n",statusValue);
statusValue = SearchBST(T, 93, NULL, &p);
printf("查找%d是否成功:%d (1->YES/0->NO)n",93,statusValue);
//
statusValue = SearchBST(T, 47, NULL, &p);
printf("查找%d是否成功:%d (1->YES/0->NO)n",47,statusValue);
statusValue = SearchBST(T, 99, NULL, &p);
printf("查找%d是否成功:%d (1->YES/0->NO)n",99,statusValue);
printf("n");
return 0;
}

以上是动态查找-二叉排序树的全部内容，来源链接： utcz.com/a/21238.html

动态查找-二叉排序树

概念

二叉排序树的查找操作

二叉排序树的插入操作

二叉排序树的删除操作

完整代码

其他人也看了：