详解Java二叉排序树
一、二叉排序树定义
1.二叉排序树的定义
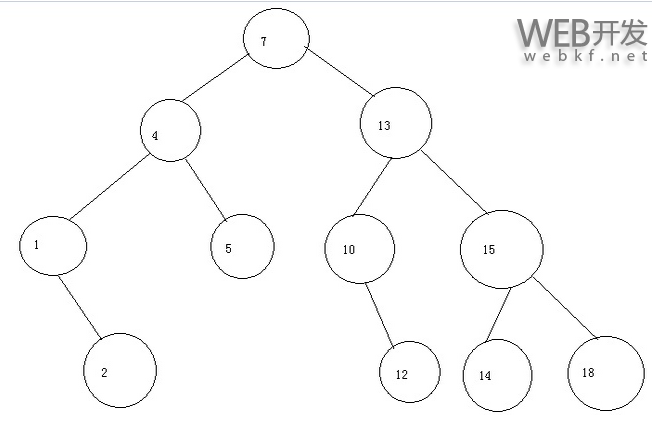
二叉排序树(Binary Sort Tree)又称二叉查找(搜索)树(Binary Search Tree)。其定义为:二叉排序树或者是空树,或者是满足如下性质的二叉树:
①若它的左子树非空,则左子树上所有结点的值均小于根结点的值;
②若它的右子树非空,则右子树上所有结点的值均大于根结点的值;
③左、右子树本身又各是一棵二叉排序树。
上述性质简称二叉排序树性质(BST性质),故二叉排序树实际上是满足BST性质的二叉树。
2.二叉排序树的性质
按中序遍历二叉排序树,所得到的中序遍历序列是一个递增有序序列。
3.二叉排序树的插入
在二叉排序树中插入新结点,要保证插入后的二叉树仍符合二叉排序树的定义。
插入过程:
若二叉排序树为空,则待插入结点*S作为根结点插入到空树中;
当非空时,将待插结点关键字S->key和树根关键字t->key进行比较,若s->key = t->key,则无须插入,若s->key< t->key,则插入到根的左子树中,若s->key> t->key,则插入到根的右子树中。而子树中的插入过程和在树中的插入过程相同,如此进行下去,直到把结点*s作为一个新的树叶插入到二叉排序树中,或者直到发现树已有相同关键字的结点为止。
4.二叉排序树的查找
假定二叉排序树的根结点指针为 root ,给定的关键字值为 K ,则查找算法可描述为:
① 置初值: q = root ;
② 如果 K = q -> key ,则查找成功,算法结束;
③ 否则,如果 K < q -> key ,而且 q 的左子树非空,则将 q 的左子树根送 q ,转步骤②;否则,查找失败,结束算法;
④ 否则,如果 K > q -> key ,而且 q 的右子树非空,则将 q 的右子树根送 q ,转步骤②;否则,查找失败,算法结束。
5.二叉排序树的删除
假设被删结点是*p,其双亲是*f,不失一般性,设*p是*f的左孩子,下面分三种情况讨论:
⑴ 若结点*p是叶子结点,则只需修改其双亲结点*f的指针即可。
⑵ 若结点*p只有左子树PL或者只有右子树PR,则只要使PL或PR 成为其双亲结点的左子树即可。
⑶ 若结点*p的左、右子树均非空,先找到*p的中序前趋(或后继)结点*s(注意*s是*p的左子树中的最右下的结点,它的右链域为空),然后有两种做法:① 令*p的左子树直接链到*p的双亲结点*f的左链上,而*p的右子树链到*p的中序前趋结点*s的右链上。② 以*p的中序前趋结点*s代替*p(即把*s的数据复制到*p中),将*s的左子树链到*s的双亲结点*q的左(或右)链上。
6、二叉树的遍历
二叉树的遍历有三种方式,如下:
(1)前序遍历(DLR),首先访问根结点,然后遍历左子树,最后遍历右子树。简记根-左-右。
(2)中序遍历(LDR),首先遍历左子树,然后访问根结点,最后遍历右子树。简记左-根-右。
(3)后序遍历(LRD),首先遍历左子树,然后遍历右子树,最后访问根结点。简记左-右-根。
二、代码编写
1、树节点类的定义0
package com.lin;
/**
* 功能概要:
*/
public class TreeNode {
public Integer data;
/*该节点的父节点*/
public TreeNode parent;
/*该节点的左子节点*/
public TreeNode left;
/*该节点的右子节点*/
public TreeNode right;
public TreeNode(Integer data) {
this.data = data;
}
@Override
public String toString() {
return "TreeNode [data=" + data + "]";
}
}
2、二叉排序树的定义
package com.lin;
/**
* 功能概要:排序/平衡二叉树
*/
public class SearchTree {
public TreeNode root;
public long size;
/**
* 往树中加节点
* @param data
* @return Boolean 插入成功返回true
*/
public Boolean addTreeNode(Integer data) {
if (null == root) {
root = new TreeNode(data);
System.out.println("数据成功插入到平衡二叉树中");
return true;
}
TreeNode treeNode = new TreeNode(data);// 即将被插入的数据
TreeNode currentNode = root;
TreeNode parentNode;
while (true) {
parentNode = currentNode;// 保存父节点
// 插入的数据比父节点小
if (currentNode.data > data) {
currentNode = currentNode.left;
// 当前父节点的左子节点为空
if (null == currentNode) {
parentNode.left = treeNode;
treeNode.parent = parentNode;
System.out.println("数据成功插入到二叉查找树中");
size++;
return true;
}
// 插入的数据比父节点大
} else if (currentNode.data < data) {
currentNode = currentNode.right;
// 当前父节点的右子节点为空
if (null == currentNode) {
parentNode.right = treeNode;
treeNode.parent = parentNode;
System.out.println("数据成功插入到二叉查找树中");
size++;
return true;
}
} else {
System.out.println("输入数据与节点的数据相同");
return false;
}
}
}
/**
* @param data
* @return TreeNode
*/
public TreeNode findTreeNode(Integer data){
if(null == root){
return null;
}
TreeNode current = root;
while(current != null){
if(current.data > data){
current = current.left;
}else if(current.data < data){
current = current.right;
}else {
return current;
}
}
return null;
}
}
这里暂时只放了一个增加和查找的方法
3、前、中、后遍历
package com.lin;
import java.util.Stack;
/**
* 功能概要:
*/
public class TreeOrder {
/**
* 递归实现前序遍历
* @author linbingwen
* @since 2015年8月29日
* @param treeNode
*/
public static void preOrderMethodOne(TreeNode treeNode) {
if (null != treeNode) {
System.out.print(treeNode.data + " ");
if (null != treeNode.left) {
preOrderMethodOne(treeNode.left);
}
if (null != treeNode.right) {
preOrderMethodOne(treeNode.right);
}
}
}
/**
* 循环实现前序遍历
* @param treeNode
*/
public static void preOrderMethodTwo(TreeNode treeNode) {
if (null != treeNode) {
Stack<TreeNode> stack = new Stack<TreeNode>();
stack.push(treeNode);
while (!stack.isEmpty()) {
TreeNode tempNode = stack.pop();
System.out.print(tempNode.data + " ");
// 右子节点不为null,先把右子节点放进去
if (null != tempNode.right) {
stack.push(tempNode.right);
}
// 放完右子节点放左子节点,下次先取
if (null != tempNode.left) {
stack.push(tempNode.left);
}
}
}
}
/**
* 递归实现中序遍历
* @param treeNode
*/
public static void medOrderMethodOne(TreeNode treeNode){
if (null != treeNode) {
if (null != treeNode.left) {
medOrderMethodOne(treeNode.left);
}
System.out.print(treeNode.data + " ");
if (null != treeNode.right) {
medOrderMethodOne(treeNode.right);
}
}
}
/**
* 循环实现中序遍历
* @param treeNode
*/
public static void medOrderMethodTwo(TreeNode treeNode){
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode current = treeNode;
while (current != null || !stack.isEmpty()) {
while(current != null) {
stack.push(current);
current = current.left;
}
if (!stack.isEmpty()) {
current = stack.pop();
System.out.print(current.data+" ");
current = current.right;
}
}
}
/**
* 递归实现后序遍历
* @param treeNode
*/
public static void postOrderMethodOne(TreeNode treeNode){
if (null != treeNode) {
if (null != treeNode.left) {
postOrderMethodOne(treeNode.left);
}
if (null != treeNode.right) {
postOrderMethodOne(treeNode.right);
}
System.out.print(treeNode.data + " ");
}
}
/**
* 循环实现后序遍历
* @param treeNode
*/
public static void postOrderMethodTwo(TreeNode treeNode){
if (null != treeNode) {
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode current = treeNode;
TreeNode rightNode = null;
while(current != null || !stack.isEmpty()) {
while(current != null) {
stack.push(current);
current = current.left;
}
current = stack.pop();
while (current != null && (current.right == null ||current.right == rightNode)) {
System.out.print(current.data + " ");
rightNode = current;
if (stack.isEmpty()){
System.out.println();
return;
}
current = stack.pop();
}
stack.push(current);
current = current.right;
}
}
}
}
4、使用方法
package com.lin;
/**
* 功能概要:
*/
public class SearchTreeTest {
/**
* @param args
*/
public static void main(String[] args) {
SearchTree tree = new SearchTree();
tree.addTreeNode(50);
tree.addTreeNode(80);
tree.addTreeNode(20);
tree.addTreeNode(60);
tree.addTreeNode(10);
tree.addTreeNode(30);
tree.addTreeNode(70);
tree.addTreeNode(90);
tree.addTreeNode(100);
tree.addTreeNode(40);
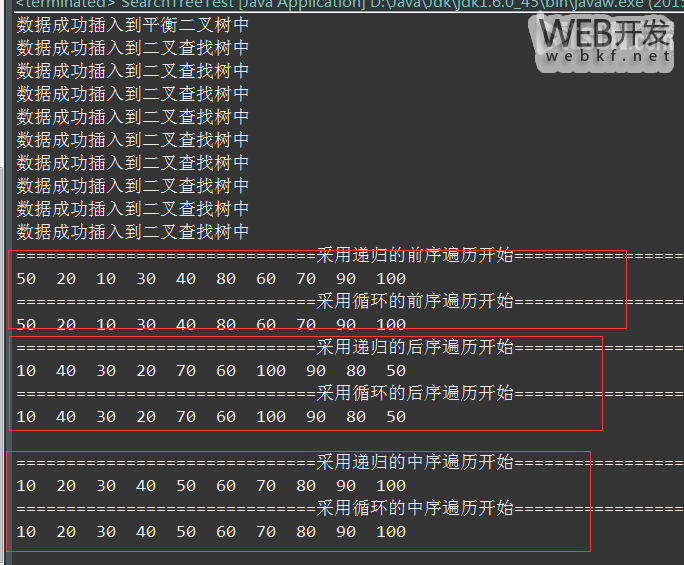
System.out.println("=============================="+"采用递归的前序遍历开始"+"==============================");
TreeOrder.preOrderMethodOne(tree.root);
System.out.println();
System.out.println("=============================="+"采用循环的前序遍历开始"+"==============================");
TreeOrder.preOrderMethodTwo(tree.root);
System.out.println();
System.out.println("=============================="+"采用递归的后序遍历开始"+"==============================");
TreeOrder.postOrderMethodOne(tree.root);
System.out.println();
System.out.println("=============================="+"采用循环的后序遍历开始"+"==============================");
TreeOrder.postOrderMethodTwo(tree.root);
System.out.println();
System.out.println("=============================="+"采用递归的中序遍历开始"+"==============================");
TreeOrder.medOrderMethodOne(tree.root);
System.out.println();
System.out.println("=============================="+"采用循环的中序遍历开始"+"==============================");
TreeOrder.medOrderMethodTwo(tree.root);
}
}
输出结果:
同样,进行查找过程如下:
TreeNode node = tree.findTreeNode(100);
System.out.println(node);
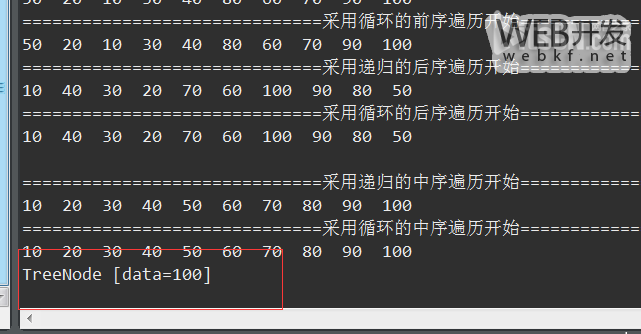
结果是正确的
以上就是关于Java二叉排序树的详细介绍,希望对大家的学习java程序设计有所帮助。
以上是 详解Java二叉排序树 的全部内容, 来源链接: utcz.com/p/208065.html