【Web前端问题】关于尾递归的问题
引子
设 m、n 为正整数,
- 当乘积
mn等于0时,函数f(m, n)等于m + n + 1, - 否则
f(m, n)等于f(m - 1, f(m, n - 1))。
下面是上述问题的一段简单代码(Javascript)
javascriptfunction f(m, n) {if (m * n == 0) {
return m + n + 1
}
return f(m - 1, f(m , n - 1))
}
console.log(f(2, 1)) // 5
疑惑
摘自电子书ECMA6 入门中的 尾递归 的定义:
函数调用自身,称为递归。如果尾调用自身,就称为尾递归。
引子代码中的函数f是return了自身,但是其第二个参数又调用f,那么在这种情况下,
- 函数
f算不算是尾递归呢? - 如果
f不是尾递归,又如何改成尾递归(如能改)?
回答:
不是尾递归。。 f(m , n - 1)执行结束后需要向上层返回执行结果,也就是把结果给f(m - 1, f(m, n - 1))然后继续递归。。那么程序运行时必然会保存f函数上一层的状态,所以这跟普通递归一样的
回答:
这个无法转换成尾递归或者循环,实际上也无法在递归里缓存用到的值,实际上m稍微一大就会导致f(m,n)的结果极大,很快就超出long double精度了。
事实上在JS里,f(3,1022)就已经超出了JS的最大数Infinity,f(3,1021)的结果等于 1.5729814930045264e+308,
f(4,3)更是天文数字,值为 7*2^(2.358995333375681e+67) - 3,试想一下2的这么多次方就觉得吓尿了,远超过Infinity。
f(5,1)=f(4,f(5,0))=f(4,6)更是远超过f(4,3),所以后面都不用计算了,全是Infinity
用JS实现楼主的题目,我们可以总结出通项式来
javascriptfunction f(m,n){if(m===0 || n===0) return m+n+1;
if(m===1){
return n+2;
}else if(m===2){
return 2*n+3;
}else if(m===3){
return 7*Math.pow(2,n)-3;
}else if(m===4){
// 递归一下f3的通项式
function f4(n){
var f3=function(x){return 7*Math.pow(2,x)-3}
if(n==0)return 5;
return f3(f4(n-1));
}
return f4(n);
}
return Infinity;
}
速度当然是非常快的,楼主可以用自己递归的实现和我上面的实现执行一下f(2,5600)试试,差别相当大,而且递归的实现,如果用f(2,6000)就会爆栈,call stack太多。
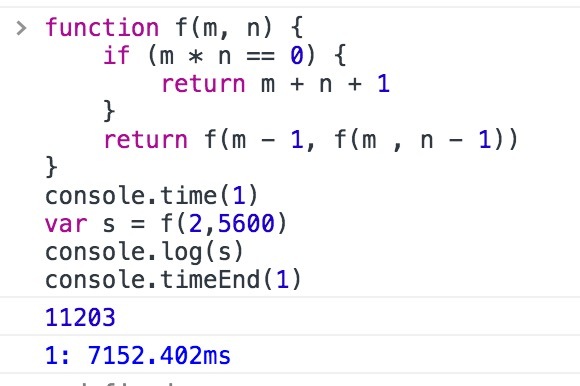
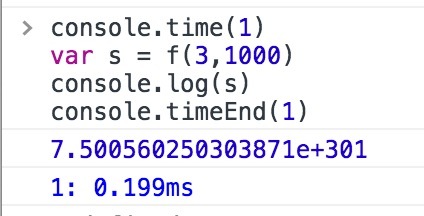
看一下速度
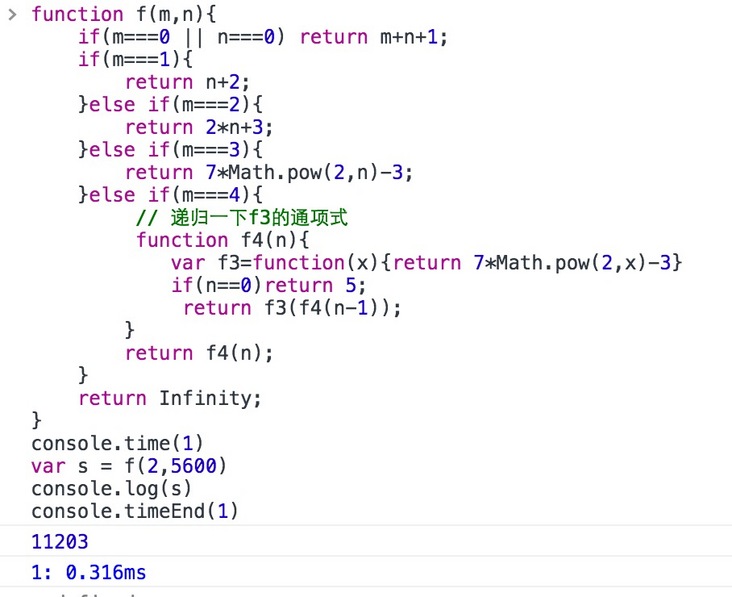
还有递归根本执行不了的这个
回答:
题目里面的不是尾递归,因为函数的最后实际相当于如下形式,很显然不是尾递归。
var r = f(m , n - 1);return f(m - 1, r);
而把这个函数改造成尾递归是可行的,实际上任何函数都可以改造成尾递归形式。
function f(m, n) { function cps(m, n, cb) {
if (m*n == 0) {
cb(m + n + 1)
return
}
cps(m, n - 1, function(r) {
cps(m - 1, r, cb)
})
}
var result
cps(m, n, function(r) {
result = r
})
return result
}
不过可惜的是,javascript 不支持尾递归优化,改成这种形式之后反而因为增加了中间层次导致挂的更快,所以这个变换在 javascript 里面也只有理论意义而已。
回答:
當且僅當尾調用自身。
return f(m - 1, f(m , n - 1)) 中的 f(m , n - 1) 顯然不是尾調用。
以上是 【Web前端问题】关于尾递归的问题 的全部内容, 来源链接: utcz.com/a/141799.html