【Web前端问题】求这个算法如何实现?
数据格式如下:
[ {
"event": {
"id": "2013",
"startTime": "00:57:00",
"endTime": "07:56:00",
"title": "list 1",
"backgroundColor": "#f6c79f",
"textColor": "#8c725b",
"order": 2014
}
},
{
"event": {
"id": "2016",
"startTime": "00:51:59",
"endTime": "06:57:00",
"title": "list 2",
"backgroundColor": "#a7bff7",
"textColor": "#5f6d8c",
"order": 2017
}
},
{
"event": {
"id": "2019",
"startTime": "00:11:00",
"endTime": "11:35:00",
"title": "list 3",
"backgroundColor": "#beea91",
"textColor": "#728c57",
"order": 2020
}
},
{
"event": {
"id": "2022",
"startTime": "09:01:00",
"endTime": "13:18:00",
"title": "list 4",
"backgroundColor": "#d1b1ff",
"textColor": "#73618c",
"order": 2023
}
}
]
需求描述:
在1天的坐标地图上(00:00 - 24:00),绘制每个数据,
可能得示意图如下: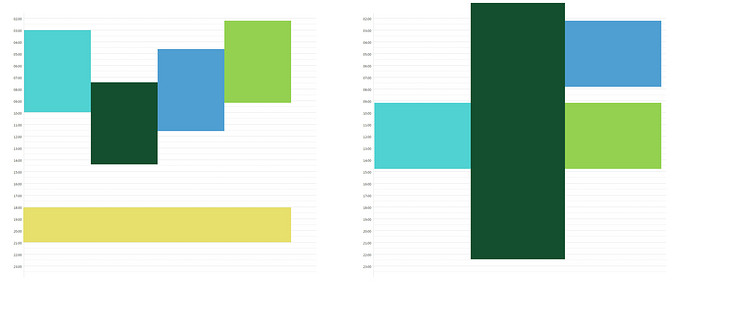
1.根据数据的startTime和endTime可以求得数据在 Y 轴上的坐标(表现为top以及height值,已实现)
2.由于每个时间段都可能相交(一个事件的时间段(startTime - endTime)的一部分在另个一个事件的时间段中,叫做相交),则在 X 轴上相交的事件平分X轴的宽度(表现为left和width值)
2.1.如果一个事件没有与任何事件相交,则这个事件的宽度是100%
2.2 如果相交平分的话,必须order越大,位置越靠前
2.3 一个事件可能和另一个事件相交,也可能和另外几个事件相交
我的问题是如何实现X轴平分宽度且定位left的算法?也就是每个元素的left和width值得算法
补充内容:A与B相交,B与C相交,A与C不相交,则ABC也是平分
回答:
大致写了一下,基本思路是
先将全部task按order从大到小排序(此部分省略)
按start end生成task对象, 使用figure对象的add_one,依次添加到figure中。
插入一个对象时,判断已有对象中与其相重叠的对象,使其left为最大的重叠对象的left+1,同时更新最大width
最后使用is_overlap方法检测tasks中的没有与任何事件相交的事件,并标记出来,这些事件left设为0,width设为100%,除了这些事件以外的事件,宽度设为1/max_width, left设为 1/max_width*(left-1) (这一部省略)
以下代码为2和3的步骤
function task(start, end) { var _this = this;
this.start = start;
this.end = end;
this.left = 0;
this.width = 0;
this.is_overlap = function (t1, t2) {
return !((t1 < _this.start && t2 < _this.start ) || (t1 > _this.end && t2 > _this.end));
}
}
function figure() {
var _this = this;
this.tasks = [];
this.max_width = 0;
this.add_one = function (obj) {
var overlap = [];
var max_left = 0;
for(var i = 0; i < _this.tasks.length; i++) {
if (_this.tasks[i].is_overlap(obj.start, obj.end)){
overlap.push(_this.tasks[i]);
}
}
for(var i = 0; i < overlap.length; i++) {
max_left = Math.max(overlap[i].left, max_left);
}
obj.left = max_left + 1;
_this.max_width = Math.max(obj.left, _this.max_width);
_this.tasks.push(obj);
}
}
var fig = new figure();
var tasks = [];
tasks[0] = new task(3, 10);
tasks[1] = new task(8, 14);
tasks[2] = new task(5, 12);
tasks[3] = new task(2, 9);
tasks[4] = new task(18, 21);
// tasks[0] = new task(9, 15);
// tasks[1] = new task(0, 22);
// tasks[2] = new task(3, 7);
// tasks[3] = new task(9, 15);
for (var i = 0; i< tasks.length; i++){
fig.add_one(tasks[i]);
}
for (var i = 0; i< fig.tasks.length; i++){
console.log('index: '+ i +' left: ' + fig.tasks[i].left);
}
console.log('width :'+fig.max_width);
回答:
二维分组
先纵向分组(
VGroups)。凡之间有相交关系的事件分入同一组。各组之间是独立的(组间不相交)。分组算法是:将每个事件看做节点,若两个节点相交,则连一条边。这样得到一个图,分组即求此图的连通分量。可以用深度优先搜索或者广度优先搜索等算法求连通分量。纵向组内再横向分组(
HGroups)。凡之间没有相交关系的事件分入同一组(组内不相交)。这一步的作用是压缩可以并列显示的事件数,利用没有占用的空间。
这样在纵横两个维度分组后,再转换成图形就是直截了当了。
测试
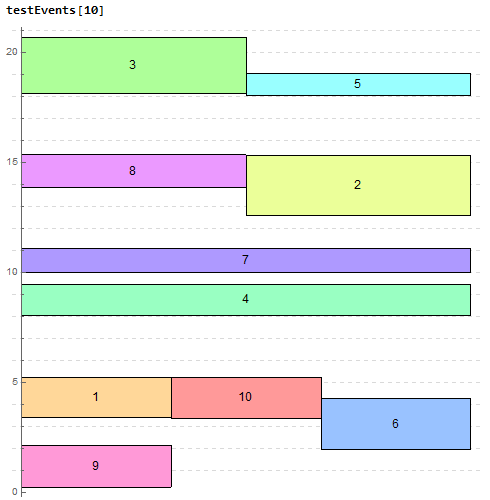
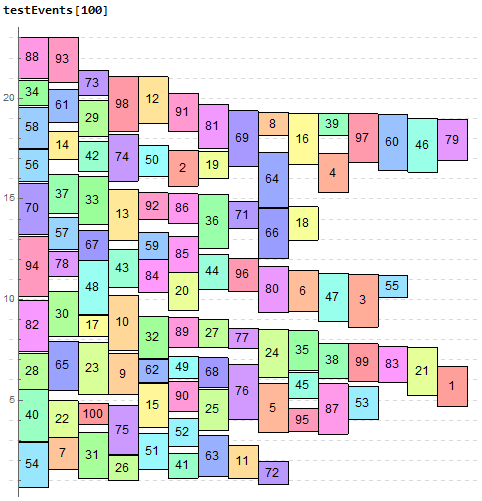
附:Mahematica 代码
renderEvents[evts_List] := Map[SortBy[-#duration &] /* renderVGroup]@
ConnectedComponents@
RelationGraph[{e1, e2} \[Function]
IntervalIntersection[e1["duration"], e2["duration"]] =!=
Interval[], evts]
renderVGroup[evts_List] := Module[{hgs, n},
hgs = Last@
NestWhile[{Rest@First@#,
addToGroups[Last@#, First@First@#]} &, {evts, {}},
First[#] != {} &];
n = Length[hgs];
MapIndexed[renderHGroup[#1, (First[#2] - 1)/n, 1/n] &]@hgs]
addToGroups[gs_List, e_] := Module[{p},
p = FirstPosition[gs,
g_ /;
IntervalIntersection[IntervalUnion @@ (#duration & /@ g),
e["duration"]] === Interval[],
Missing["NotFound"], {1}, Heads -> False];
If[Head[p] === Missing,
Append[gs, {e}],
ReplacePart[gs, First[p] -> Append[gs[[First[p]]], e]]]]
renderHGroup[evts_List, x_, w_] :=
Map[{#["color"],
Rectangle[{x, Min[#["duration"]]}, {x + w, Max[#["duration"]]}],
Black, Text[
Style[#["title"],
Medium], {x + w/2, (Max[#["duration"]] + Min[#["duration"]])/
2}]} &, evts]
testEvents[n_] := Module[{events},
events =
Table[<|"title" -> ToString[i],
"duration" -> Interval[{#, # + #2}] &[RandomReal[{0, 21}],
RandomReal[{1, 3}]], "color" -> Hue[i/n, 0.4],
"order" -> i|>, {i, n}];
Graphics[{EdgeForm[Thin], renderEvents[events]}, AspectRatio -> 1,
GridLines -> {None, Range[24]},
GridLinesStyle -> {LightGray, Dashed}, Axes -> {None, True}]]
回答:
@saigyouyou
有可能是这样的

回答:
small water : 我觉得flex布局不需要考虑横向平分问题.
以上是 【Web前端问题】求这个算法如何实现? 的全部内容, 来源链接: utcz.com/a/140861.html