java数字图像处理常用算法(转)

前些时候做毕业设计,用java做的数字图像处理方面的东西,这方面的资料ms比较少,发点东西上来大家共享一下,主要就是些算法,有自己写的,有人家的,还有改人家的,有的算法写的不好,大家不要见笑。
一 读取bmp图片数据
// 获取待检测图像 ,数据保存在数组 nData[],nB[] ,nG[] ,nR[]中
public void getBMPImage(String source) throws Exception {
clearNData(); //清除数据保存区
FileInputStream fs = null;
try {
fs = new FileInputStream(source);
int bfLen = 14;
byte bf[] = new byte[bfLen];
fs.read(bf, 0, bfLen); // 读取14字节BMP文件头
int biLen = 40;
byte bi[] = new byte[biLen];
fs.read(bi, 0, biLen); // 读取40字节BMP信息头
// 源图宽度
nWidth = (((int) bi[7] & 0xff) << 24)
| (((int) bi[6] & 0xff) << 16)
| (((int) bi[5] & 0xff) << 8) | (int) bi[4] & 0xff;
// 源图高度
nHeight = (((int) bi[11] & 0xff) << 24)
| (((int) bi[10] & 0xff) << 16)
| (((int) bi[9] & 0xff) << 8) | (int) bi[8] & 0xff;
// 位数
nBitCount = (((int) bi[15] & 0xff) << 8) | (int) bi[14] & 0xff;
// 源图大小
int nSizeImage = (((int) bi[23] & 0xff) << 24)
| (((int) bi[22] & 0xff) << 16)
| (((int) bi[21] & 0xff) << 8) | (int) bi[20] & 0xff;
// 对24位BMP进行解析
if (nBitCount == 24){
int nPad = (nSizeImage / nHeight) - nWidth * 3;
nData = new int[nHeight * nWidth];
nB=new int[nHeight * nWidth];
nR=new int[nHeight * nWidth];
nG=new int[nHeight * nWidth];
byte bRGB[] = new byte[(nWidth + nPad) * 3 * nHeight];
fs.read(bRGB, 0, (nWidth + nPad) * 3 * nHeight);
int nIndex = 0;
for (int j = 0; j < nHeight; j++){
for (int i = 0; i < nWidth; i++) {
nData[nWidth * (nHeight - j - 1) + i] = (255 & 0xff) << 24
| (((int) bRGB[nIndex + 2] & 0xff) << 16)
| (((int) bRGB[nIndex + 1] & 0xff) << 8)
| (int) bRGB[nIndex] & 0xff;
nB[nWidth * (nHeight - j - 1) + i]=(int) bRGB[nIndex]& 0xff;
nG[nWidth * (nHeight - j - 1) + i]=(int) bRGB[nIndex+1]& 0xff;
nR[nWidth * (nHeight - j - 1) + i]=(int) bRGB[nIndex+2]& 0xff;
nIndex += 3;
}
nIndex += nPad;
}
// Toolkit kit = Toolkit.getDefaultToolkit();
// image = kit.createImage(new MemoryImageSource(nWidth, nHeight,
// nData, 0, nWidth));
/*
//调试数据的读取
FileWriter fw = new FileWriter("C:\\Documents and Settings\\Administrator\\My Documents\\nDataRaw.txt");//创建新文件
PrintWriter out = new PrintWriter(fw);
for(int j=0;j<nHeight;j++){
for(int i=0;i<nWidth;i++){
out.print((65536*256+nData[nWidth * (nHeight - j - 1) + i])+"_"
+nR[nWidth * (nHeight - j - 1) + i]+"_"
+nG[nWidth * (nHeight - j - 1) + i]+"_"
+nB[nWidth * (nHeight - j - 1) + i]+" ");
}
out.println("");
}
out.close();
*/
}
}
catch (Exception e) {
e.printStackTrace();
throw new Exception(e);
}
finally {
if (fs != null) {
fs.close();
}
}
// return image;
}
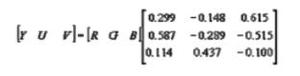
二 由r g b 获取灰度数组
public int[] getBrightnessData(int rData[],int gData[],int bData[]){
int brightnessData[]=new int[rData.length];
if(rData.length!=gData.length || rData.length!=bData.length
|| bData.length!=gData.length){
return brightnessData;
}
else {
for(int i=0;i<bData.length;i++){
double temp=0.3*rData[i]+0.59*gData[i]+0.11*bData[i];
brightnessData[i]=(int)(temp)+((temp-(int)(temp))>0.5?1:0);
}
return brightnessData;
}
}
三 直方图均衡化
public int [] equilibrateGray(int[] PixelsGray,int width,int height)
{
int gray;
int length=PixelsGray.length;
int FrequenceGray[]=new int[length];
int SumGray[]=new int[256];
int ImageDestination[]=new int[length];
for(int i = 0; i <length ;i++)
{
gray=PixelsGray[i];
FrequenceGray[gray]++;
}
// 灰度均衡化
SumGray[0]=FrequenceGray[0];
for(int i=1;i<256;i++){
SumGray[i]=SumGray[i-1]+FrequenceGray[i];
}
for(int i=0;i<256;i++) {
SumGray[i]=(int)(SumGray[i]*255/length);
}
for(int i=0;i<height;i++)
{
for(int j=0;j<width;j++)
{
int k=i*width+j;
ImageDestination[k]=0xFF000000 | ((SumGray[PixelsGray[k]]<<
16 ) | (SumGray[PixelsGray[k]]<< 8 ) | SumGray[PixelsGray[k]]);
}
}
return ImageDestination;
}
四 laplace2阶滤波,增强边缘,图像锐化
public int[] laplace2DFileter(int []data,int width,int height){
int filterData[]=new int[data.length];
int min=10000;
int max=-10000;
for(int i=0;i<height;i++){
for(int j=0;j<width;j++){
if(i==0 || i==height-1 || j==0 || j==width-1)
filterData[i*width+j]=data[i*width+j];
else
filterData[i*width+j]=9*data[i*width+j]-data[i*width+j-1]-data[i*width+j+1]
-data[(i-1)*width+j]-data[(i-1)*width+j-1]-data[(i-1)*width+j+1]
-data[(i+1)*width+j]-data[(i+1)*width+j-1]-data[(i+1)*width+j+1];
if(filterData[i*width+j]<min)
min=filterData[i*width+j];
if(filterData[i*width+j]>max)
max=filterData[i*width+j];
}
}
// System.out.println("max: "+max);
// System.out.println("min: "+min);
for(int i=0;i<width*height;i++){
filterData[i]=(filterData[i]-min)*255/(max-min);
}
return filterData;
}
五 laplace2阶增强滤波,增强边缘,增强系数delt
public int[] laplaceHigh2DFileter(int []data,int width,int height,double delt){
int filterData[]=new int[data.length];
int min=10000;
int max=-10000;
for(int i=0;i<height;i++){
for(int j=0;j<width;j++){
if(i==0 || i==height-1 || j==0 || j==width-1)
filterData[i*width+j]=(int)((1+delt)*data[i*width+j]);
else
filterData[i*width+j]=(int)((9+delt)*data[i*width+j]-data[i*width+j-1])-data[i*width+j+1]
-data[(i-1)*width+j]-data[(i-1)*width+j-1]-data[(i-1)*width+j+1]
-data[(i+1)*width+j]-data[(i+1)*width+j-1]-data[(i+1)*width+j+1];
if(filterData[i*width+j]<min)
min=filterData[i*width+j];
if(filterData[i*width+j]>max)
max=filterData[i*width+j];
}
}
for(int i=0;i<width*height;i++){
filterData[i]=(filterData[i]-min)*255/(max-min);
}
return filterData;
}
六 局部阈值处理2值化
// 局部阈值处理2值化,niblack's method
/*原理:
T(x,y)=m(x,y) + k*s(x,y)
取一个宽度为w的矩形框,(x,y)为这个框的中心。
统计框内数据,T(x,y)为阈值,m(x,y)为均值,s(x,y)为均方差,k为参数(推荐-2)计算出t再对(x,y)进行切割255/0。
这个算法的优点是 速度快,效果好。
缺点是 niblack's method会产生一定的噪声。
*/
public int[] localThresholdProcess(int []data,int width,int height,int w,int h,double coefficients,double gate){
int[] processData=new int[data.length];
for(int i=0;i<data.length;i++){
processData[i]=255;
}
if(data.length!=width*height)
return processData;
int wNum=width/w;
int hNum=height/h;
int delt[]=new int[w*h];
//System.out.println("w; "+w+" h:"+h+" wNum:"+wNum+" hNum:"+hNum);
for(int j=0;j<hNum;j++){
for(int i=0;i<wNum;i++){
//for(int j=0;j<1;j++){
// for(int i=0;i<1;i++){
for(int n=0;n<h;n++)
for(int k=0;k<w;k++){
delt[n*w+k]=data[(j*h+n)*width+i*w+k];
//System.out.print("delt["+(n*w+k)+"]: "+delt[n*w+k]+" ");
}
//System.out.println();
/*
for(int n=0;n<h;n++)
for(int k=0;k<w;k++){
System.out.print("data["+((j*h+n)*width+i*w+k)+"]: "+data[(j*h+n)*width+i*w+k]+" ");
}
System.out.println();
*/
delt=thresholdProcess(delt,w,h,coefficients,gate);
for(int n=0;n<h;n++)
for(int k=0;k<w;k++){
processData[(j*h+n)*width+i*w+k]=delt[n*w+k];
// System.out.print("delt["+(n*w+k)+"]: "+delt[n*w+k]+" ");
}
//System.out.println();
/*
for(int n=0;n<h;n++)
for(int k=0;k<w;k++){
System.out.print("processData["+((j*h+n)*width+i*w+k)+"]: "+processData[(j*h+n)*width+i*w+k]+" ");
}
System.out.println();
*/
}
}
return processData;
}
七 全局阈值处理2值化
public int[] thresholdProcess(int []data,int width,int height,double coefficients,double gate){
int [] processData=new int[data.length];
if(data.length!=width*height)
return processData;
else{
double sum=0;
double average=0;
double variance=0;
double threshold;
if( gate!=0){
threshold=gate;
}
else{
for(int i=0;i<width*height;i++){
sum+=data[i];
}
average=sum/(width*height);
for(int i=0;i<width*height;i++){
variance+=(data[i]-average)*(data[i]-average);
}
variance=Math.sqrt(variance);
threshold=average-coefficients*variance;
}
for(int i=0;i<width*height;i++){
if(data[i]>threshold)
processData[i]=255;
else
processData[i]=0;
}
return processData;
}
}
八 垂直边缘检测,sobel算子
public int[] verticleEdgeCheck(int []data,int width,int height,int sobelCoefficients) throws Exception{
int filterData[]=new int[data.length];
int min=10000;
int max=-10000;
if(data.length!=width*height)
return filterData;
try{
for(int i=0;i<height;i++){
for(int j=0;j<width;j++){
if(i==0 || i==1 || i==height-1 || i==height-2
||j==0 || j==1 || j==width-1 || j==width-2){
filterData[i*width+j]=data[i*width+j];
}
else{
double average;
//中心的九个像素点
//average=data[i*width+j]-Math.sqrt(2)*data[i*width+j-1]+Math.sqrt(2)*data[i*width+j+1]
average=data[i*width+j]-sobelCoefficients*data[i*width+j-1]+sobelCoefficients*data[i*width+j+1]
-data[(i-1)*width+j-1]+data[(i-1)*width+j+1]
-data[(i+1)*width+j-1]+data[(i+1)*width+j+1];
filterData[i*width+j]=(int)(average);
}
if(filterData[i*width+j]<min)
min=filterData[i*width+j];
if(filterData[i*width+j]>max)
max=filterData[i*width+j];
}
}
for(int i=0;i<width*height;i++){
filterData[i]=(filterData[i]-min)*255/(max-min);
}
}
catch (Exception e)
{
e.printStackTrace();
throw new Exception(e);
}
return filterData;
}
九 图像平滑:3*3掩模处理(平均处理),降低噪声
public int[] filter(int []data,int width,int height) throws Exception{
int filterData[]=new int[data.length];
int min=10000;
int max=-10000;
if(data.length!=width*height)
return filterData;
try{
for(int i=0;i<height;i++){
for(int j=0;j<width;j++){
if(i==0 || i==1 || i==height-1 || i==height-2
||j==0 || j==1 || j==width-1 || j==width-2){
filterData[i*width+j]=data[i*width+j];
}
else{
double average;
//中心的九个像素点
average=(data[i*width+j]+data[i*width+j-1]+data[i*width+j+1]
+data[(i-1)*width+j]+data[(i-1)*width+j-1]+data[(i-1)*width+j+1]
+data[(i+1)*width+j]+data[(i+1)*width+j-1]+data[(i+1)*width+j+1])/9;
filterData[i*width+j]=(int)(average);
}
if(filterData[i*width+j]<min)
min=filterData[i*width+j];
if(filterData[i*width+j]>max)
max=filterData[i*width+j];
}
}
for(int i=0;i<width*height;i++){
filterData[i]=(filterData[i]-min)*255/(max-min);
}
}
catch (Exception e)
{
e.printStackTrace();
throw new Exception(e);
}
return filterData;
}
以上是 java数字图像处理常用算法(转) 的全部内容, 来源链接: utcz.com/z/394262.html