广度优先搜索
图遍历是按某种系统顺序访问图的所有顶点的问题。遍历图主要有两种方法。
广度优先搜索(BFS)从图G的第0层顶点X开始。然后,我们访问与X相邻的所有顶点。访问后,我们将这些顶点标记为“已访问”,并将它们放置在第-层1。然后,我们从1级顶点开始,并对每个1级顶点应用相同的方法,依此类推。当访问图的每个顶点时,BFS遍历就会终止。
BFS算法
该概念是在访问邻居顶点的其他邻居顶点之前访问所有邻居顶点。
将所有节点的状态初始化为“就绪”。
将源顶点放在队列中,并将其状态更改为“等待”。
重复以下两个步骤,直到队列为空-
从队列中删除第一个顶点,并将其标记为“已访问”。
将状态为“就绪”的已删除顶点的所有邻居添加到队列的尾部。将其状态标记为“正在等待”。
问题
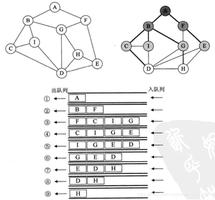
让我们拍一个图(源顶点为“ a”),然后应用BFS算法找出遍历顺序。
解决方案-
将所有顶点的状态初始化为“就绪”。
把一个在队列,并且改变其状态为“等待”。
从队列中删除一个,将其标记为“已访问”。
添加一个“邻居‘准备就绪’状态B,d和ē结束队列,并将其标记为‘等待’。
从队列中删除b,将其标记为“已访问”,将其“就绪”邻居c放置在队列末尾,并将c标记为“等待”。
从队列中删除d并将其标记为“已访问”。它没有邻居处于“就绪”状态。
从队列中删除e并将其标记为“访问”。它没有邻居处于“就绪”状态。
从队列中删除c并将其标记为“访问”。它没有邻居处于“就绪”状态。
队列为空,请停止。
因此遍历顺序为-
a→b→d→e→c
遍历的替代顺序是-
a→b→e→d→c
或a→d→b→e→c
或a→e→b→d→c
或a→b→e→d→c
或a→d→e→b→c
BFS的应用
寻找最短路径
非加权图的最小生成树
GPS导航系统
在无向图中检测周期
查找一个连接的组件中的所有节点
复杂度分析
令G(V,E)为| V |的图 顶点数和| E | 边数。如果广度优先搜索算法访问图形中的每个顶点并检查每个边缘,则其时间复杂度将为-
O(| V | + | E |)。O(| E |)
它可能在O(1)和O(| V2 |)之间变化
以上是 广度优先搜索 的全部内容, 来源链接: utcz.com/z/352534.html