Java实现快速排序算法的完整示例

Z时代
2024-01-10
分类：综合

首先，来看一下，快速排序的实现的动态图：

快速排序介绍：

快速排序，根据教科书说法来看，是冒泡排序的一种改进。

快速排序，由一个待排序的数组（array），以及找准三个变量：

中枢值（pivot）

左值（left）

右值（right）

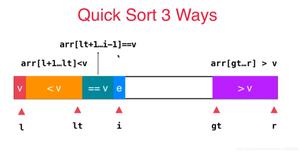
根据中枢值（pivot）来做调整，将数组（array）分为三个部分：

第一部分：中枢值（pivot），单独数字构成，这个值在每次排序好的"最中间"；

第二部分：左边数组（由array的一部分组成），这个数组在第一部分中枢值（pivot）的"左边"，其中左边数组中的每一个值（不一定是排序好的，可能是乱序的），都要比中枢值和右边数组的值要小；

第三部分：右边数组（由array的一部分组成），这个数组在第一部分中枢值（pivot）的"右边"，其中右边数组的每一个值（不一定是排序好的，可能是乱序的），都要比中枢值和左边数组的值要大

再根据递归思想，对左边数组、中枢值、右边数组不断递归循环操作，不断拆分出三部分来，最终达到快速排序的效果。

核心逻辑：

快排算法递归调用：

接下来附上完整实现代码：


public class QuickSort {
 /**
  * 快速排序调用方法
  *
  * @param ary 待排序数组
  * @param left 左值
  * @param right 右值
  * @return int值
  * @author Cansluck
  */
 public static int getSortNum(int[] ary, int left, int right) {
  // 定义一个中枢值pivot，让其等于数组的左值，枢轴选定后永远不变，最终在中间，前小后大
  int pivot = ary[left];
  while (left < right) {
   // 看后面ary[right] > pivot比较，如果右边数组值大于中枢值，说明不需要调整位置，则让右值（right）自减1
   while (left < right && ary[right] >= pivot) {
    right--; // 执行自减操作
   }
   // 如果上面循环不符合条件的，则说明右边数组的一个值，小于中枢值（pivot），则将其替换到左边数组中
   ary[left] = ary[right];
   // 看后面ary[left] < pivot比较，如果左边数组值小于中枢值，说明不需要调整位置，则让左值（left）自增1
   while (left < right && ary[left] <= pivot) {
    left++; // 执行自增操作
   }
   // 如果上面循环不符合条件，则说明左边数组的一个值，大于中枢值（pivot），则将其替换到右边数组中
   ary[right] = ary[left];
  }
  // 最后将中枢值给自增后的左边数组的一个值中
  ary[left] = pivot;
  // 返回左边数组下标
  return left;
 }
 /**
  * 快速排序递归方法
  *
  * @author Cansluck
  * @param ary 待排序数组
  * @param left 左值
  * @param right 右值
  */
 public static void quickSort(int[] ary, int left, int right) {
  // 定义中枢值
  int pivot;
  // 判断
  if (left < right) {
   // 根据方法得到了每次中枢值的位置
   pivot = getSortNum(ary, left, right);
   // 根据中枢值（pivot），来对左边数组进行递归调用快速排序
   quickSort(ary, left, pivot - 1);
   // 根据中枢值（pivot），来对右边数组进行递归调用快速排序
   quickSort(ary, pivot + 1, right);
  }
 }
 public static void main(String[] args) {
  int[] ary = {97, 58, 12, 88, 77, 22, 33, 44, 66, 22};
  quickSort(ary, 0, ary.length - 1);
  for (int i = 0; i < ary.length; i++) {
   if (i != ary.length - 1)
    System.out.print(ary[i] + ", ");
   else
    System.out.println(ary[i]);
  }
 }
}