Java编程实现基于图的深度优先搜索和广度优先搜索完整代码
为了解15puzzle问题,了解了一下深度优先搜索和广度优先搜索。先来讨论一下深度优先搜索(DFS),深度优先的目的就是优先搜索距离起始顶点最远的那些路径,而广度优先搜索则是先搜索距离起始顶点最近的那些路径。我想着深度优先搜索和回溯有什么区别呢?百度一下,说回溯是深搜的一种,区别在于回溯不保留搜索树。那么广度优先搜索(BFS)呢?它有哪些应用呢?答:最短路径,分酒问题,八数码问题等。言归正传,这里笔者用java简单实现了一下广搜和深搜。其中深搜是用图+栈实现的,广搜使用图+队列实现的,代码如下:
1.新建一个表示“无向图”类NoDirectionGraph
package com.wly.algorithmbase.datastructure;
/**
* 无向图
* @author wly
*
*/
public class NoDirectionGraph {
private int mMaxSize;
//图中包含的最大顶点数
private GraphVertex[] vertexList;
//顶点数组
private int[][] indicatorMat;
//指示顶点之间的连通关系的邻接矩阵
private int nVertex;
//当前实际保存的顶点数目
public NoDirectionGraph(int maxSize) {
mMaxSize = maxSize;
vertexList = new GraphVertex[mMaxSize];
indicatorMat = new int[mMaxSize][mMaxSize];
nVertex = 0;
//初始化邻接矩阵元素为0
for (int j=0;j<mMaxSize;j++) {
for (int k=0;k<mMaxSize;k++) {
indicatorMat[j][k] = 0;
}
}
}
public void addVertex(GraphVertex v) {
if(nVertex < mMaxSize) {
vertexList[nVertex++] = v;
} else {
System.out.println("---插入失败,顶点数量已达上限!");
}
}
/**
* 修改邻接矩阵,添加新的边
* @param start
* @param end
*/
public void addEdge(int start,int end) {
indicatorMat[start][end] = 1;
indicatorMat[end][start] = 1;
}
/**
* 打印邻接矩阵
*/
public void printIndicatorMat() {
for (int[] line:indicatorMat) {
for (int i:line) {
System.out.print(i + " ");
}
System.out.println();
}
}
/**
* 深度优先遍历
* @param vertexIndex 表示要遍历的起点,即图的邻接矩阵中的行数
*/
public void DFS(int vertexIndex) {
ArrayStack stack = new ArrayStack();
//1.添加检索元素到栈中
vertexList[vertexIndex].setVisited(true);
stack.push(vertexIndex);
int nextVertexIndex = getNextVertexIndex(vertexIndex);
while(!stack.isEmpty()) {
//不断地压栈、出栈,直到栈为空(检索元素也没弹出了栈)为止
if(nextVertexIndex != -1) {
vertexList[nextVertexIndex].setVisited(true);
stack.push(nextVertexIndex);
stack.printElems();
} else {
stack.pop();
}
//检索当前栈顶元素是否包含其他未遍历过的节点
if(!stack.isEmpty()) {
nextVertexIndex = getNextVertexIndex(stack.peek());
}
}
}
/**
* 得到当前顶点的下一个顶点所在行
* @param column
* @return
*/
public int getNextVertexIndex(int column) {
for (int i=0;i<indicatorMat[column].length;i++) {
if(indicatorMat[column][i] == 1 && !vertexList[i].isVisited()) {
return i;
}
}
return -1;
}
/**
* 广度优先遍历
* @param vertexIndex 表示要遍历的起点,即图的邻接矩阵中的行数
*/
public void BFS(int vertexIndex) {
ChainQueue queue = new ChainQueue();
vertexList[vertexIndex].setVisited(true);
queue.insert(new QueueNode(vertexIndex));
int nextVertexIndex = getNextVertexIndex(vertexIndex);
while(!queue.isEmpty()) {
if(nextVertexIndex != -1) {
vertexList[nextVertexIndex].setVisited(true);
queue.insert(new QueueNode(nextVertexIndex));
} else {
queue.remove();
}
if(!queue.isEmpty()) {
nextVertexIndex = getNextVertexIndex(queue.peek().data);
queue.printElems();
}
}
}
}
2.然后是一个用数组模拟的栈ArrayStack
package com.wly.algorithmbase.datastructure;
/**
* 使用数组实现栈结构
* @author wly
*
*/
public class ArrayStack {
private int[] tArray;
private int topIndex = -1;
//表示当前栈顶元素的索引位置
private int CAPACITY_STEP = 12;
//数组容量扩展步长
public ArrayStack() {
/***创建泛型数组的一种方法***/
tArray = new int[CAPACITY_STEP];
}
/**
* 弹出栈顶元素方法
* @return
*/
public int pop() {
if(isEmpty()) {
System.out.println("错误,栈中元素为空,不能pop");
return -1;
} else {
int i = tArray[topIndex];
tArray[topIndex--] = -1;
//擦除pop元素
return i;
}
}
/**
* 向栈中插入一个元素
* @param t
*/
public void push(int t) {
//检查栈是否已满
if(topIndex == (tArray.length-1)) {
//扩展容量
int[] tempArray = new int[tArray.length + CAPACITY_STEP];
for (int i=0;i<tArray.length;i++) {
tempArray[i] = tArray[i];
}
tArray = tempArray;
tempArray = null;
} else {
topIndex ++;
tArray[topIndex] = t;
}
}
/**
* 得到栈顶元素,但不弹出
* @return
*/
public int peek() {
if(isEmpty()) {
System.out.println("错误,栈中元素为空,不能peek");
return -1;
} else {
return tArray[topIndex];
}
}
/**
* 判断当前栈是否为空
* @return
*/
public Boolean isEmpty() {
return (topIndex < 0);
}
/**
* 打印栈中元素
*/
public void printElems() {
for (int i=0;i<=topIndex;i++) {
System.out.print(tArray[i] + " ");
}
System.out.println();
}
}
3.在一个用链表模拟的队列ChainQueue
package com.wly.algorithmbase.datastructure;
/**
* 使用链表实现队列
*
* @author wly
*
*/
public class ChainQueue {
private QueueNode head;
// 指向队列头节点
private QueueNode tail;
// 指向队列尾节点
private int size = 0;
// 队列尺寸
public ChainQueue() {
}
/**
* 插入新节点到队列尾
*/
public void insert(QueueNode node) {
// 当然也可以这么写,添加tail.prev = node
if (head == null) {
head = node;
tail = head;
} else {
node.next = tail;
tail.prev = node;
// 双向连接,确保head.prev不为空
tail = node;
}
size++;
}
/**
* 移除队列首节点
*/
public QueueNode remove() {
if (!isEmpty()) {
QueueNode temp = head;
head = head.prev;
size--;
return temp;
} else {
System.out.println("异常操作,当前队列为空!");
return null;
}
}
/**
* 队列是否为空
*
* @return
*/
public Boolean isEmpty() {
if (size > 0) {
return false;
} else {
return true;
}
}
/**
* 返回队列首节点,但不移除
*/
public QueueNode peek() {
if (!isEmpty()) {
return head;
} else {
System.out.println();
System.out.println("异常操作,当前队列为空!");
return null;
}
}
/**
* 返回队列大小
*
* @return
*/
public int size() {
return size;
}
/**
* 打印队列中的元素
*/
public void printElems() {
QueueNode tempNode = head;
while(tempNode != null) {
System.out.print(tempNode.data + " ");
tempNode = tempNode.prev;
}
System.out.println();
}
}
/**
* 节点类
*
* @author wly
*
*/
class QueueNode {
QueueNode prev;
QueueNode next;
int data;
public QueueNode(int data) {
this.data = data;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
@Override
public String toString() {
// TODO Auto-generated method stub
super.toString();
return data + "";
}
}
4.测试一下Test_BFS_DFS
package com.wly.algorithmbase.search;
import com.wly.algorithmbase.datastructure.GraphVertex;
import com.wly.algorithmbase.datastructure.NoDirectionGraph;
/**
* 基于图的深度优先搜索
* @author wly
*
*/
public class Test_BFS_DFS {
public static void main(String[] args) {
//初始化测试数据
NoDirectionGraph graph = new NoDirectionGraph(7);
graph.addVertex(new GraphVertex("A"));
graph.addVertex(new GraphVertex("B"));
graph.addVertex(new GraphVertex("C"));
graph.addVertex(new GraphVertex("D"));
graph.addVertex(new GraphVertex("E"));
graph.addVertex(new GraphVertex("F"));
graph.addVertex(new GraphVertex("G"));
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(3, 6);
graph.addEdge(2, 5);
System.out.println("--图的邻接矩阵--");
graph.printIndicatorMat();
//测试深搜
System.out.println("--深度优先搜索--");
graph.DFS(0);
graph = new NoDirectionGraph(7);
graph.addVertex(new GraphVertex("A"));
graph.addVertex(new GraphVertex("B"));
graph.addVertex(new GraphVertex("C"));
graph.addVertex(new GraphVertex("D"));
graph.addVertex(new GraphVertex("E"));
graph.addVertex(new GraphVertex("F"));
graph.addVertex(new GraphVertex("G"));
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(3, 6);
graph.addEdge(2, 5);
System.out.println("--广度优先搜索--");
graph.BFS(0);
}
}
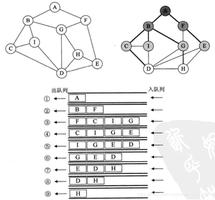
这里测试的图结构如下:
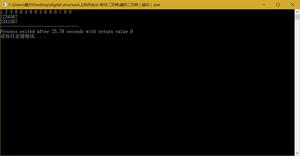
运行结果如下:
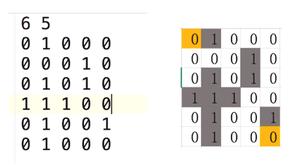
--图的邻接矩阵--
0 1 1 0 0 0 0
1 0 0 1 1 0 0
1 0 0 0 0 1 0
0 1 0 0 0 0 1
0 1 0 0 0 0 0
0 0 1 0 0 0 0
0 0 0 1 0 0 0
--深度优先搜索--
0 1
0 1 3
0 1 3 6
0 1 4
0 2
0 2 5
--广度优先搜索--
0 1
0 1 2
1 2
1 2 3
1 2 3 4
2 3 4
2 3 4 5
3 4 5
3 4 5 6
4 5 6
5 6
6
这里需要说明一下上面深搜和广搜的运行结果,其中0,1,2,3…分别对应着A,B,C,D...有点绕哈,,见谅~~
O啦~~~
总结
以上是 Java编程实现基于图的深度优先搜索和广度优先搜索完整代码 的全部内容, 来源链接: utcz.com/z/339904.html