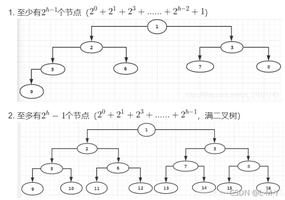
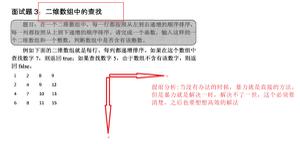
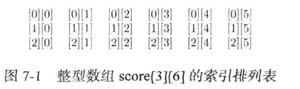
python分治法求二维数组局部峰值方法
题目的意思大致是在一个n*m的二维数组中,找到一个局部峰值。峰值要求大于相邻的四个元素(数组边界以外视为负无穷),比如最后我们找到峰值A[j][i],则有A[j][i] > A[j+1][i] && A[j][i] > A[j-1][i] && A[j][i] > A[j][i+1] && A[j][i] > A[j][i-1]。返回该峰值的坐标和值。
当然,最简单直接的方法就是遍历所有数组元素,判断是否为峰值,时间复杂度为O(n^2)
再优化一点求每一行(列)的最大值,再通过二分法找最大值列的峰值(具体方法可见一维数组求峰值),这种算法时间复杂度为O(logn)
这里讨论的是一种复杂度为O(n)的算法,算法思路分为以下几步:
1、找“田”字。包括外围的四条边和中间横竖两条边(图中绿色部分),比较其大小,找到最大值的位置。(图中的7)
2、找到田字中最大值后,判断它是不是局部峰值,如果是返回该坐标,如果不是,记录找到相邻四个点中最大值坐标。通过该坐标所在的象限缩小范围,继续比较下一个田字
3、当范围缩小到3*3时必定会找到局部峰值(也可能之前就找到了)
关于为什么我们选择的范围内一定存在峰值,大家可以这样想,首先我们有一个圈,我们已知有圈内至少有一个元素大于这个圈所有的元素,那么,是不是这个圈中一定有一个最大值?
可能说得有点绕,但是多想想应该能够理解,也可以用数学的反证法来证明。
算法我们理解后接下来就是代码实现了,这里我用的语言是python(初学python,可能有些用法上不够简洁请见谅),先上代码:
import numpy as np
def max_sit(*n): #返回最大元素的位置
temp = 0
sit = 0
for i in range(len(n)):
if(n[i]>temp):
temp = n[i]
sit = i
return sit
def dp(s1,s2,e1,e2):
m1 = int((e1-s1)/2)+s1 #row
m2 = int((e2-s1)/2)+s2 #col
nub = e1-s1
temp = 0
sit_row = 0
sit_col = 0
for i in range(nub):
t = max_sit(list[s1][s2+i], #第一排
list[m1][s2+i], #中间排
list[e1][s2+i], #最后排
list[s1+i][s2], #第一列
list[s1+i][m2], #中间列
list[s1+i][e2], #最后列
temp)
if(t==6):
pass
elif(t==0):
temp = list[s1][s2+i]
sit_row = s1
sit_col = s2+i
elif(t==1):
temp = list[m1][s2+i]
sit_row = m1
sit_col = s2+i
elif(t==2):
temp = list[e1][s2+i]
sit_row = e1
sit_col = s2+i
elif(t==3):
temp = list[s1+i][s2]
sit_row = s1+i
sit_row = s2
elif(t==4):
temp = list[s1+i][m2]
sit_row = s1+i
sit_col = m2
elif(t==5):
temp = list[s1+i][e2]
sit_row = s1+i
sit_col = m2
t = max_sit(list[sit_row][sit_col], #中
list[sit_row-1][sit_col], #上
list[sit_row+1][sit_col], #下
list[sit_row][sit_col-1], #左
list[sit_row][sit_col+1]) #右
if(t==0):
return [sit_row-1,sit_col-1]
elif(t==1):
sit_row-=1
elif(t==2):
sit_row+=1
elif(t==3):
sit_col-=1
elif(t==4):
sit_col+=1
if(sit_row<m1):
e1 = m1
else:
s1 = m1
if(sit_col<m2):
e2 = m2
else:
s2 = m2
return dp(s1,s2,e1,e2)
f = open("demo.txt","r")
list = f.read()
list = list.split("\n") #对行进行切片
list = ["0 "*len(list)]+list+["0 "*len(list)] #加上下的围墙
for i in range(len(list)): #对列进行切片
list[i] = list[i].split()
list[i] = ["0"]+list[i]+["0"] #加左右的围墙
list = np.array(list).astype(np.int32)
row_n = len(list)
col_n = len(list[0])
ans_sit = dp(0,0,row_n-1,col_n-1)
print("找到峰值点位于:",ans_sit)
print("该峰值点大小为:",list[ans_sit[0]+1,ans_sit[1]+1])
f.close()
首先我的输入写在txt文本文件里,通过字符串转换变为二维数组,具体转换过程可以看我上一篇博客——python中字符串转换为二维数组。(需要注意的是如果在windows环境中split后的列表没有空尾巴,所以不用加list.pop()这句话)。有的变动是我在二维数组四周加了“0”的围墙。加围墙可以再我们判断峰值的时候不用考虑边界问题。
max_sit(*n)函数用于找到多个值中最大值的位置,返回其位置,python的内构的max函数只能返回最大值,所以还是需要自己写,*n表示不定长参数,因为我需要在比较田和十(判断峰值)都用到这个函数
def max_sit(*n): #返回最大元素的位置
temp = 0
sit = 0
for i in range(len(n)):
if(n[i]>temp):
temp = n[i]
sit = i
return sit
dp(s1,s2,e1,e2)函数中四个参数的分别可看为startx,starty,endx,endy。即我们查找范围左上角和右下角的坐标值。
m1,m2分别是row 和col的中间值,也就是田字的中间。
def dp(s1,s2,e1,e2):
m1 = int((e1-s1)/2)+s1 #row
m2 = int((e2-s1)/2)+s2 #col
依次比较3行3列中的值找到最大值,注意这里要求二维数组为正方形,如果为矩形需要做调整
for i in range(nub):
t = max_sit(list[s1][s2+i], #第一排
list[m1][s2+i], #中间排
list[e1][s2+i], #最后排
list[s1+i][s2], #第一列
list[s1+i][m2], #中间列
list[s1+i][e2], #最后列
temp)
if(t==6):
pass
elif(t==0):
temp = list[s1][s2+i]
sit_row = s1
sit_col = s2+i
elif(t==1):
temp = list[m1][s2+i]
sit_row = m1
sit_col = s2+i
elif(t==2):
temp = list[e1][s2+i]
sit_row = e1
sit_col = s2+i
elif(t==3):
temp = list[s1+i][s2]
sit_row = s1+i
sit_row = s2
elif(t==4):
temp = list[s1+i][m2]
sit_row = s1+i
sit_row = m2
elif(t==5):
temp = list[s1+i][e2]
sit_row = s1+i
sit_row = m2
判断田字中最大值是不是峰值,并找不出相邻最大值
t = max_sit(list[sit_row][sit_col], #中
list[sit_row-1][sit_col], #上
list[sit_row+1][sit_col], #下
list[sit_row][sit_col-1], #左
list[sit_row][sit_col+1]) #右
if(t==0):
return [sit_row-1,sit_col-1]
elif(t==1):
sit_row-=1
elif(t==2):
sit_row+=1
elif(t==3):
sit_col-=1
elif(t==4):
sit_col+=1
缩小范围,递归求解
if(sit_row<m1):
e1 = m1
else:
s1 = m1
if(sit_col<m2):
e2 = m2
else:
s2 = m2
return dp(s1,s2,e1,e2)
好了,到这里代码基本分析完了。如果还有不清楚的地方欢迎下方留言。
除了这种算法外,我也写一种贪心算法来求解这道题,只可惜最坏的情况下算法复杂度还是O(n^2),QAQ。
大体的思路就是从中间位置起找相邻4个点中最大的点,继续把该点来找相邻最大点,最后一定会找到一个峰值点,有兴趣的可以看一下,上代码:
#!/usr/bin/python3
def dp(n):
temp = (str[n],str[n-9],str[n-1],str[n+1],str[n+9]) #中 上 左 右 下
sit = temp.index(max(temp))
if(sit==0):
return str[n]
elif(sit==1):
return dp(n-9)
elif(sit==2):
return dp(n-1)
elif(sit==3):
return dp(n+1)
else:
return dp(n+9)
f = open("/home/nancy/桌面/demo.txt","r")
list = f.read()
list = list.replace(" ","").split() #转换为列表
row = len(list)
col = len(list[0])
str="0"*(col+3)
for x in list: #加围墙 二维变一维
str+=x+"00"
str+="0"*(col+1)
mid = int(len(str)/2)
print(str,mid)
p = dp(mid)
print (p)
f.close()
以上这篇python分治法求二维数组局部峰值方法就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持。
以上是 python分治法求二维数组局部峰值方法 的全部内容, 来源链接: utcz.com/z/333230.html