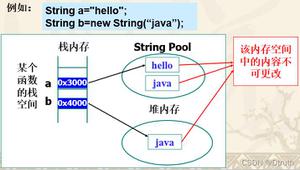
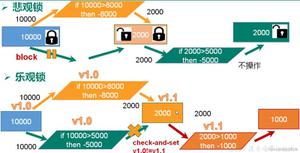
在C ++中无需使用递归或欧几里得算法即可找到两个数字的HCF

  • Z时代
  • 2024-01-10
  • 分类：综合

众所周知，HCF或GCD可以使用欧几里得算法" title="欧几里得算法">欧几里得算法轻松计算。但是在这里，我们将看到如何在不使用欧几里得算法或任何递归算法的情况下生成GCD或HCF。假设两个数字分别为16和24。这两个的GCD为8。

这里的方法很简单。如果这两个数中较大的数可被较小的数整除，则为HCF，否则从（较小的2）开始为1，如果当前元素将两个数相除，则为HCF。

示例

#include <iostream>
using namespace std;
int gcd(int a, int b) {
   int min_num = min(a, b);
   if (a % min_num == 0 && b % min_num == 0)
   return min_num;
   for (int i = min_num / 2; i >= 2; i--) {
      if (a % i == 0 && b % i == 0)
      return i;
   }
   return 1;
}
int main() {
   int a = 16, b = 24;
   cout << "HCF: "<< gcd(a, b);
}

输出结果

HCF: 8

以上是 在C ++中无需使用递归或欧几里得算法即可找到两个数字的HCF 的全部内容， 来源链接： utcz.com/z/331269.html

回到顶部