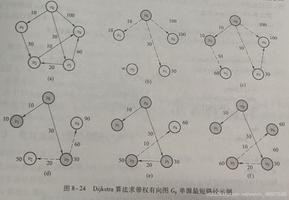
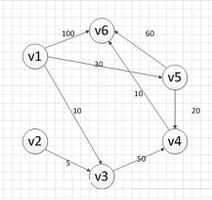
Dijkstra算法的复杂度

Z时代
2024-01-10
分类：问答

我从许多资料中获悉，如果使用幼稚的方法来获取min元素（线性搜索），Dijkstra的最短路径也将以O（V ^

2）复杂度运行。但是，如果使用优先级队列，则可以将其优化为O（VLogV），因为此数据结构将在O（1）时间返回min元素，但是在删除min元素之后需要O（LogV）时间来恢复堆属性。

我已经在以下链接中针对UVA问题的以下代码中实现了Dijkstra的算法：https

//uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=16&page=show_problem&problem

=1927：

#include<iostream>
#include<vector>
#include <climits>
#include <cmath>
#include <set>
using namespace std;
#define rep(a,b,c) for(int c=a;c<b;c++)
typedef std::vector<int> VI;
typedef std::vector<VI> VVI;
struct cmp {
    bool operator()(const pair<int,int> &a,const pair<int,int> &b) const {
        return a.second < b.second;
    }
};
void sp(VVI &graph,set<pair<int,int>,cmp> &minv,VI &ans,int S,int T) {
    int e = -1;
    minv.insert(pair<int,int>(S,0));
    rep(0,graph.size() && !minv.empty() && minv.begin()->first != T,s) {
        e = minv.begin()->first;
        minv.erase(minv.begin());
        int nb = 0;
        rep(0,graph[e].size(),d) {
            nb = d;
            if(graph[e][d] != INT_MAX && ans[e] + graph[e][d] < ans[d]) {
                set<pair<int,int>,cmp>::iterator si = minv.find(pair<int,int>(d,ans[d]));
                if(si != minv.end())
                    minv.erase(*si);
                ans[d] = ans[e] + graph[e][d];
                minv.insert(pair<int,int>(d,ans[d]));
            }
        }
    }
}
int main(void) {
    int cc = 0,N = 0,M = 0,S = -1,T = -1,A=-1,B=-1,W=-1;
    VVI graph;
    VI ans;
    set<pair<int,int>,cmp> minv;
    cin >> cc;
    rep(0,cc,i) {
        cin >> N >> M >> S >> T;
        graph.clear();
        ans.clear();
        graph.assign(N,VI());
        ans.assign(graph.size(),INT_MAX);
        minv.clear();
        rep(0,N,j) {
            graph[j].assign(N,INT_MAX);
        }
        ans[S] = 0;
        graph[S][S] = 0;
        rep(0,M,j) {
            cin >> A >> B >> W;
            graph[A][B] = min(W,graph[A][B]);
            graph[B][A] = min(W,graph[B][A]);
        }
        sp(graph,minv,ans,S,T);
        cout << "Case #" << i + 1 << ": ";
        if(ans[T] != INT_MAX)
            cout << ans[T] << endl;
        else
            cout << "unreachable" << endl;
    }
}