C++ Dijkstra算法之求图中任意两顶点的最短路径
Dijkstra算法是图中找任意两点中最短路径的一种经典算法。
重点的步骤总结如下:
1.算法采用了并查集 (之后都叫它为 最短路径顶点集 ):即每次都找离开始顶点距离最短的顶点,然后把该顶点加入最短路径顶点集中(已经加入最短路径顶点集里的那些顶点 下一次就会跳过它了,并且,在顶点集里 任意两个顶点间的距离 都已经是最短)
2.用来记录从源点(开始顶点) 到vi (0<=i<=numVertices) 的最短距离 的数组dist[numVertices] ,并且这个数组的元素值是会不断变化的,为什么呢,因为,这个最短距离无非两种情况。
第一种:开始顶点v直接到达目的顶点X的距离。
第二种:开始顶点v先到达中间顶点Vk(Vk可能不止一个)再到目的顶点的距离。
要么是第一种情况最短,要么是第二种情况最短,因此需要再这两者间选择一个最小值作为最短路径。
dist[w] = min {dist[w] ,dist[k] + this->getWeight(k,w)};
3.路径数组path[],这个数组 保存了从源点到终点vi 的最短路径上该顶点的前驱顶点的序号,即:会记录最短路径 某个顶点的上一个 顶点是什么,比如说 path[4]的值是2,那么 4的上一个顶点 就是2 ,path[2]的顶点比如是3 那么2的上一个顶点就是3 ,继续, 如果path[3]是0那么 这个路径为: , 因此,当Dijkstra算法结束的时候,我们只需要从最后那个顶点开始 path[endVertexce] 就可以得到它上一个顶点的下标,然后一直找,直到找到源点,那么这个路径就输出完了.
Dijkstra算法求带权有向图单元最短路径的示例过程图如下:

图a为 本次的示例图,然后假如要从v0出发,去找顶点v4的最短距离.首先,我们可以看到图b 伸出三条虚线,是什么意思呢?就是因为v0 和这三个顶点都连通,然后,找一个最短和v0相连的顶点,发现是v1,权值是10,然后接下来的要做什么呢??接下来就是重点了,要从v1出发,去寻找所有与v1 相连的顶点,如果源点到 v1 后再到这些顶点的距离 比 源点直接到 这些 和v1相连的顶点 的距离 短的话
就要重新修改v0到 vx的值(x为任意与v1相连的顶点),即v0—>v1—>v2,一开始v0不能直接到v2所以dist[2]=∞,但是v0->v1->v2的值却为60,因此dist[2]的值就改为60,即v0通过“某条路径”抵达 v2的当前最短路径就是60,为什么说是当前呢,因为等下可能还有其他 未加入最短路径顶点集 的某个顶点,他可能从源点,再经过它 再到v2 ,比 从源点出发到 v1 再到v2的距离更小!(比如说v3)。接着重复以上操作:在未加入"最短路径顶点集" 里 找一个离源点最近的 顶点,然后让它加入”最短路径顶点集“里 因为刚才加入的是v1,它的权值是10 ,然后v1里没有能够到达v3的边,所以,v3的值没有改变,如果v3的值要改变的话:当且仅当从源点 到最小权值顶点再到 v3 因此,v0到v3已经是最小的路径了,因此,把它加入 最短路径顶点集里, 加入到最短路径顶点集里,任意两个顶点之间的距离 都已经是最短路径, v3加到顶点集之后要做的事情 还是和刚才那样:不断去寻找和它相连接的顶点Vx,然后比较 v0直接到Vx的距离是否比 v0 先到v3再到 Vx的距离大,如果是,做两件事情:
① 修改dist[x] 的值(即v0通过某一条路径到达Vx的最短路径 这里如果前提条件成立 这条路径为: v0—>v3—>Vx).
②修改路径数组path[x]=index(v3)=3 (下标0对应v0,下标1对应v1…),即让x这个位置的顶点的前驱的下标索引为3,即v3的下标索引.
Dijkstra算法的思想就是像上述一样,未完成的步骤留给读者完成。
具体测试代码如下(有些代码与Dijkstra算法无关,代码是基于之前实现的代码,如果是DevC++ 编译器,可以按住Ctrl +鼠标左键 点击主函数的测试代码的函数,可以跳到对应 的函数代码体,见谅见谅.)
本次路径的输出利用了栈,使得路径可以按从起点到终点 按顺序 输出。
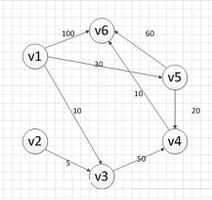
本次测试图如下:

代码如下:
#include<iostream>
#include<cstring>
#include<math.h>
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
const long long int maxWeight = RAND_MAX; //无穷大的值
const int DefaultVertices = 30; //最大顶点数不妨设为30
template <class T, class E>
class Graph {
protected:
int maxVertices=10;//图中最大顶点数
int numVertices=0;//图中当前顶点数
int numEdges=0;//图中当前边数
bool direction=false;//图中边的是否有方向
bool withCost=false;//图中的边是否带权
//返回顶点名vertex的序号(从0开始)
int getVertexPos (T vertex);
public:
void DFS (const T& v)
{
}
void BFS (const T& v)
{
}
Graph(int sz , bool direct, bool cost); //构造函数
~Graph()//析构函数
{}
//析构函数
bool GraphEmpty () const //判图是否为空,因为不需要修改,因此设置为常成员函数
{
return numEdges == 0;
}
bool GraphFull() const; //判图是否为满
//返回图中当前顶点数
int NumberOfVertices ()
{
return numVertices;
}
//返回图中当前边数
int NumberOfEdges ()
{
return numEdges;
}
//取回序号为 i 的顶点值(顶点名)
virtual T getValue (int i){
}
//取顶点序号为v1,v2的边上权值
virtual E getWeight (int v1, int v2){
}
//取顶点 v 的第一个邻接顶点序号
virtual int getFirstNeighbor (int v){
}
//返回顶点 v 和邻接顶点 w 的下一个邻接顶点序号
virtual int getNextNeighbor (int v, int w){
}
//插入新顶点, 点名为vertex
virtual bool insertVertex (const T vertex){
}
//插入新边(v1,v2), 权值cost
virtual bool insertEdge (T v1, T v2, E cost){
}
//删除名为 v 的顶点和所有与它相关联的边
virtual bool removeVertex (T v){
}
//在图中删除边(v1,v2)
virtual bool removeEdge (T v1, T v2){
}
};
template<class T , class E>
Graph<T,E>::Graph (int sz , bool direct, bool cost)
{
sz = DefaultVertices, direct=false, cost=false;
}
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
template <class T, class E> //
class Edge_Vertices { //边结点的类定义
public:
int dest; //边的邻接(终)点序号
E cost; //边上的权值
Edge_Vertices<T, E>* link;//下一个连接顶点
Edge_Vertices (int num=0, Edge_Vertices<T, E>* next=NULL, E weight=NULL) //构造函数
: dest (num), link (next), cost (weight) { }
bool operator != (Edge_Vertices<T, E>& R) const
{ return dest != R.dest; } //重载!=运算符,判边不等
};
template <class T, class E>
class Vertex { //顶点的类定义
public:
T data; //源顶点的名字(数据)
Edge_Vertices<T, E>* next=NULL; //next指针用来连接顶点
};
//邻接表图的类定义继承图类
template <class T, class E>
class Graphlnk : public Graph<T, E>{
public:
void Enter (void); //输入图中顶点和边信息
void Print (void); //输出图中顶点和边信息
//源顶点表 (各边链表的源顶点)
Vertex<T, E>* NodeTable;
int *path;
int *dist;
//返回名为vertex的顶点在图中的序号(从0开始),
//若未找到,则返回-1
int getVertexPos (const T vertx) //找到目标顶点所在的序号 期中 vertx 参数为string 类型
{ for (int i = 0; i < this->numVertices; i++)
if (NodeTable[i].data == vertx) return i;
return -1;
} //构造函数
Graphlnk( int sz=DefaultVertices, bool direct=false, bool cost=false );
~Graphlnk(); //析构函数
T getValue (int i) { //取序号为 i 的顶点名
return (i >= 0 && i < this->numVertices) ?
NodeTable[i].data : NULL;
}
E getWeight (int v1, int v2); //取边(v1,v2)权值
bool insertVertex (const T& vertex); //插入名为vertex的新顶点
bool removeVertex (int v); //删除序号为 v 的顶点
bool insertEdge (T in ,T out, E cost); //插入新边
bool removeEdge (int v1, int v2); //删除边(v1,v2)
int getFirstNeighbor (int v);//取顶点v的首邻接顶点 ###本次代码这两条都没有用到
int getNextNeighbor (int v, int w);//取w下一邻接点 ###本次代码这两条都没有用到
void DFS(const T &v);
void BFS(const T &v);
void DFS (int v, bool visited[]);
void BFS(int v , bool visited[]);
void Connected_Component();
void Dijkstra (int v );
void Print(int v, int w);
};
// 输出顶点 v 到顶点 w 的最短路径
//和最短路径长度。int* path;
// E** dist; 为类数据成员
template<typename T, typename E>
void Graphlnk<T,E>::Print(int v, int w)//输出从V 到W 的最短路径
{ //因为v和w都是 int 型,即输入类型的下标,因此,要用getValue 获得原来的输入的顶点名字
cout<<"始顶点 "<<this->getValue(v)<<" 到终顶点 "<<this->getValue(w)<<" 的最短路径为:"<<endl;
int current=w, previous;
stack<char > Road;//定义一个char类型的栈,因为是用顶点回溯 (即从 最后的一个顶点 往前找前驱顶点的,因此我们可以用栈(后进先出的特性))
//用栈后进先出的特性可以 在出栈的时候 按顺序输出从 开始顶点到目的顶点的 路径 ,如果对输出没有要求的话就不需要栈,可以直接输出
//不过输出的结果会倒置(从目的顶点 一步一步往回走 ,直到找到开始顶点)
stack<int >Road_Weight;//如果 顶点 要按顺序输出,还想输出 这两个顶点间的权值的话,那么这些权值也是倒置的,因此权值也需要利用栈的特性输出
Road.push(this->getValue(w)[0]);//因为this->getValue(w) 返回的是一个string 类型, 本次测试的顶点都是要么是单个数字名字,或者单个字母名字
// 因为是char 类型,因此只能单个字母进去,所以this->getValue(w)[0] 就是取第一个 字母/数字
while( current!=v )//如果这个顶点不等于 开始顶点的话
{
previous=path[current];//找它的上一个顶点
Road.push(this->getValue(path[current])[0]);//名字入栈
Road_Weight.push(this->getWeight(previous,current));//权值入栈
current=previous;
}
string p;//string 变量 p 用来记录前面的顶点和 做临时变量
string e;//string 变量 e 用来输出顶点名字
int q;
int x=1;//一个标志
int i = 1;//第i步
while(Road.empty()!=true)
{
//这个if 语句只运行一次,为什么呢,考虑到 奇数个顶点的话,那么,最短路径至少有两个顶点,如果第一次就把顶点输出完了
//那么后面的if语句都不会运行了,但是如果 是奇数个顶点呢? 奇数个顶点的话,程序编译不会出错,但是运行会中断, 即栈已经空了,不能弹栈了
//因此,执行一次这个if语句 就开始 对顶点一个 一个的弹栈,而不是 两个两个的弹
if(x)
{
p=Road.top();
Road.pop();
q=Road_Weight.top();
Road_Weight.pop();
e=Road.top();
Road.pop();
x=0;//让if 语句为假
cout<<"第"<<i++<<"步为: "<<"顶点"<<p<<"-->到顶点"<<e<<" 长度为: "<<q<<endl;
}
if(Road.empty()!=true)//如果栈不为空
{
p=e;//因为这个p在后面不再 用来接收 栈弹出的顶点,而是充当一个临时变量-------用上一个顶点 的末顶点 进行覆盖
e=Road.top();//取栈首顶点
Road.pop();// 弹栈
q=Road_Weight.top();//取栈里的首权值
Road_Weight.pop();
cout<<"第"<<i++<<"步为: "<<"顶点"<<p<<"-->到顶点"<<e<<" 长度为: "<<q<<endl;
}
}
cout<<"最短路径总长度为:"<<dist[w]<<endl;//输出最短路径长度
}
template<class T,class E>
//Graphlnk是一个带权有向图.数据成员E dist[v][j],
//0≤j<n, 是当前求到的从顶点v到 j的最短路 径长度,
//int path[v][j],0≤j<n, 存放求到的最短路径
void Graphlnk<T,E>::Dijkstra (int v )//Dijkstra算法,求得图任意两点间的 最短路径
{ int k;//变量k
bool *s = new bool[this->numVertices];//并查集s,标记顶点是否已经在最短路径的顶点集里
this->path=new int [this->numVertices];//路径数组(跳跃式,要用回溯才能找出整个完整的路径)
this->dist= new int [this->numVertices];//源点v到任意顶点vi的最短路径数组,
for(int i = 0 ; i < this->numVertices;i++)//初始化
{
s[i]=false;//把所有的顶点都标记为:未在最短路径顶点集
if(this->getWeight(v,i)!=maxWeight)//如果有v和vi间如果有权值的话,那么,就是说,这两点是连通的。
// 既然两点是连通的,那么,这个路径就有可能是最短的。
this->dist[i]=this->getWeight(v,i);
else //否则?就是没有连通咯,就用maxWeight赋值给他,即:如果dist[i]==maxWeight那么 就判定为两点是不连通的
dist[i]=maxWeight;
if(this->dist[i]<maxWeight||v==i)//如果有边连通,或者i==v
this->path[i]=v;//就让i这个顶点的前驱 是v (如果v==i 就让自己指向自己)
else
path[i]=-1;// 否则vi和 v 没有路,即两点间不连通
}
dist[v]=0;//首先,规定,v->v 即自己到自己的距离是0
s[v]=true;//将开始顶点v放入并查集数组中
int min;//最小路径的一个值
for(int i = 1; i <this->numVertices;i++)
{
min = maxWeight;//首先要让这个最小值足够大,然后后面的那些路径权值才会比这个值小然后把它替换为真正的"最小值"
for(int j=0;j<this->numVertices;j++)
if(!s[j]&&dist[j]<min)//如果这个顶点没有在最小路径的顶点集里面,则判定是否连通
//如果连通的话,就从这些 连通的顶点间找到一组最小的连通 顶点。
{
k=j;
min=dist[j];
}
s[k]=true;//找一个:若在原来路径上 添加一个顶点,首先,这个顶点在最短路径顶点集和之外, 其次,这个顶点沿着其余顶点回到开始顶点路径最短
for(int w = 0 ; w <this->numVertices;w++)
//从这个新加入的顶点Vnew出发,不断的去找和它相连接的顶点vi(i取任意正整数,即顶点可能不知有一个,可能是多个)
//然后看v到vi的路径短一点还是,v到Vnew再到Vi,如果是v到Vnew 再到vi 比 直接从v到vi更短的话,那么就替换 v到Vw的最小距离dist[w]
//并且规定w的前驱顶点为k ,即:path[w]=k; (此时w还没有在最短路径顶点集合里面)
//由此我们可以知道:既然每加入一个 顶点到 最短路径顶点集里面,都会执行这段代码。
//然后 都会从刚加入的那个顶点去 找遍所有 和它关联的顶点,所以,如果说这个加入的顶点如果 和目的顶点X相连,那么加入这个顶点后
// 执行下面的代码,就可以求出当前从始顶点到目的顶点X的最短路径,为什么是当前?因为这个最小是当前最小的,因为还有其他顶点未加入顶点集
//即有可能从 v出发 经过某个 未加入 最短路径顶点集合里的顶点 再到X 的路径大小 比 从v到原先那个加入 最短路径顶点集合里的顶点 再到x 的路径要小
//所以,下面的代码每次执行都会求得 一个临时的最短路径,如果顶点都加入完了,那么,自然是最短路径了
if(!s[w]&&dist[w]>(dist[k]+this->getWeight(k,w))&&this->getWeight(k,w)!=-1)
{
dist[w]=dist[k]+this->getWeight(k,w);//
path[w]=k;//让w顶点的前驱是k
}
}
delete []s ;//删除标记数组
//输出代码可以在函数体里,也可以 加一个print函数 在函数体外
// cout<<"始顶点 "<<v<<" 到终顶点 "<<w<<" 的最短路径为:终顶点 "<< w;
// int current=w, previous;
// while( current!=v )
// {
// previous=path[current];
// cout<<"路径"<<path[current];
// cout<<"最小距离"<<dist[current];
// cout<<" <-权值[ "<<getWeight(previous,current)<<" ]-顶点 "<<previous;
// current=previous;
// }
// cout<<"。最短路径总长度为:"<<dist[w]<<endl;
}
template<class T, class E>
void Graphlnk<T,E>::Connected_Component()//分别输出连通分量 和输出有向图中连通分量的个数
{ int Connected_Component_numbers=0;
bool visited[this->numVertices];
for(int i = 0 ; i <this->numVertices;i++)
visited[i]=false;//初始化这个visited 数组
for(int i =0; i < this->numVertices;i++)
{
if(!visited[i])//如果这个结点没有被访问过
{
cout<<"从"<<this->getValue(i)<<"开始的连通分量为:";
this->DFS(i,visited);
cout<<endl;
Connected_Component_numbers+=1;
}
}
if(this->direction==true)
cout<<"此有向图的连通分量为:"<<Connected_Component_numbers<<endl;
else
cout<<"此无向图的连通分量为:"<<Connected_Component_numbers<<endl;
delete [] visited;//结束后删除数组
}
//从名为 v 的顶点出发广度优先遍历
template <class T, class E>
void Graphlnk<T,E>::BFS(const T& v)
{ int i, w;
//创建访问标记数组
bool* visited = new bool[this->numVertices];
//对图中所有顶点初始化访问数组visited
for (i = 0; i < this->numVertices; i++)
visited[i] = false; //初始化为都未访问过
int loc = getVertexPos (v); //取名为 v 的顶点序号
if(loc == -1) //名为 v 的顶点未找到
cout<<"顶点 "<<v<<"没有找到,广度优先遍历失败。";
else
{
cout << getValue (loc) << ' '; //访问顶点 v
visited[loc] = true; //标记顶点 v 已访问过
//顶点 v 进队列, 实现分层访问
queue<int> q;
q.push(loc); //访问过的顶点进队列
while (!q.empty() ) //循环, 访问所有结点
{ loc = q.front();//记录当前队列第一个顶点的值
q.pop(); // 然后记录完让它出队列
w = getFirstNeighbor (loc); //取它的第一个邻接顶点
while (w != -1) //当邻接顶点w存在
{ if (!visited[w]) //如果未访问过
{ cout << getValue (w) << ' ';//访问它然后输出它
visited[w] = true; //标记此顶点已经访问过
q.push(w); //顶点w进队列
}
w = getNextNeighbor (loc, w); //取下一个邻接顶点
}
} //外层循环,判队列空否
}
delete [] visited;
}
template<class T , class E >
void Graphlnk<T,E>::DFS(const T &v)
{
int sign;
bool *visited = new bool[this->numVertices];
for(int i = 0; i <this->numVertices;i++)
{
visited[i]=false;//初始化都为为访问过
}
sign=this->getVertexPos(v);
if(sign==-1)
cout<<"顶点"<<v<<"不存在"<<"深度优先遍历失败"<<endl;
else //否则为存在
DFS(sign,visited);
delete[] visited; //深度优先遍历完成的话,就删除这个数组
}
template<class T,class E>
void Graphlnk<T,E>::DFS(int v , bool visited[])
{
cout<<this->getValue(v)<<" ";
visited[v]=true;
int w = this->getFirstNeighbor(v);
while(w!=-1)
{
if(!visited[w])//如果没有访问过为真
DFS(w,visited);
w=this->getNextNeighbor(v,w);//否则回退 然后继续搜索
}
}
template<class T,class E>
bool Graphlnk<T,E>::removeEdge (int v1, int v2)//删除边这个比较简单
{
if(v1<0||v2<0||v1>this->numVertices||v2>this->numVertices)//这种情况就是不符合,不符合就返回false
return false ;
else //否则为符合的
{
Edge_Vertices<T,E> *temp;//这是一个中间变量
temp=this->NodeTable[v1].next;//让它先等于顶点表个的下一个
while(temp)
{
if(temp->dest==v2)//如果一开始就是等于要删除的那个顶点的话(可能会有误解哦,这里不是删除边么,怎么删除顶点?)
//因为删除末顶点的话,就会少掉一条边
{
if(temp->link==NULL)//如果这条链只有这个待删除的顶点
{
this->NodeTable[v1].next=NULL;//让顶点表的那个顶点的下一个顶点指向空
delete temp; //删除这个顶点
break;//跳出循环
}
else{ //如果不为空的话
this->NodeTable[v1].next = temp->link;//让顶点表的下一个顶点指向 待删除 目标顶点的下一个
delete temp;//删除结点
break;
}
} if(temp)//防止内存访问出错
if(temp->link->dest ==v2)//不是第一个顶点是要删除的顶点 这个if 语句记作 AAAAA
{ Edge_Vertices<T,E> *temp2;//定义一个中间变量temp2
temp2=temp->link;//让temp 2指向 待删除 目标定点
temp->link=temp->link->link;//利用temp 断开 目标定点 与 子链的连接
delete temp2;//删除目标顶点
break;//跳出循环
} if(temp)//防止内存访问出错
temp=temp->link;//根据这条语句,会回到刚才 AAAAA 那个 if语句
}
//要考虑有向图和无向图哦
if(this->direction==false)//如果是无向图的话
{
temp=this->NodeTable[v2].next;
while(temp)
{ //此段代码与上面的逻辑完全相同,不再赘述
if(temp->dest==v1)
{
if(temp->link==NULL)
{
this->NodeTable[v2].next=NULL;
delete temp;
break;
}
else{
this->NodeTable[v2].next = temp->link;
delete temp;
break;
}
}
if(temp)
if(temp->link->dest ==v1)
{ Edge_Vertices<T,E> *temp2;
temp2=temp->link;
temp->link=temp->link->link;
delete temp2;
break;
} if(temp)
temp=temp->link;
}
}
}
this->numEdges--;//记得删完 边数要 -1;
return true;//删除成功返回true
}
template<class T , class E >
bool Graphlnk<T,E>::removeVertex (int v) //删除序号为 v 的顶点
{
if(v<0||v>=this->numVertices)//如果下标不符合规定
return false;
else //否则为符合
{
int del_vex_num=v;//记录这个删除的下标
if(v!=this->numVertices-1)//如果不是删除最后一个顶点的话
this->NodeTable[v]=this->NodeTable[--this->numVertices];//就用最后一个顶点顶的那条"链"替代这个待删除顶点的"链"
//如果删除的是最后一个顶点的话,自然就没有影响了
else
{
this->numVertices--;
int end_edg=0;//因为如果直接删掉这个点的话,那么这个点关联的边也要减掉
Edge_Vertices<T,E> *p;
p=this->NodeTable[v].next;
while(p)
{
if(p)
{ end_edg++;//如果有一个顶点,且不为空的话,那么涉及的边数就+1
}
p=p->link;
}
this->numEdges-=end_edg;
}
for(int i= 0 ; i < this->numVertices;i++)//此时的numVertices已经-1 ,然后对这所有的链进行操作,如果有将要删除顶点与这个顶点相连,则删除
{ Edge_Vertices<T,E> *temp;
temp=this->NodeTable[i].next;
//第一种情况:第一个连接的 顶点就是 将要删除的那个顶点
//这种情况很好做
if(temp->dest ==v)
{
if(temp->link==NULL)//如果这条链只有一个结点,然后第一个结点恰好是这个将要删除的顶点的话
{
this->NodeTable[i].next=NULL;//这样的话,直接删掉它
this->numEdges--;
}
else //否则
{
this->NodeTable[i].next=temp->link;
delete temp;//删除临时的指针变量
this->numEdges--;
}
}
else //第二种情况,就需要循环了,因为每一个顶点最多只有一个 将要删除的那个顶点的下标
{//第一个结点的dest!=v
while(temp)
{
if(temp->link)
{
if(temp->link->dest==v)//第一个的下一个顶点刚好是 这个dest 的话
{
Edge_Vertices<T,E> *temp2;
temp2=temp->link;//中间变量temp2;
temp->link=temp->link->link;//断开这个将要删除的顶点
delete temp2;//删除刚才的中间变量//
this->numEdges--;
break;
}
}
temp=temp->link;//这个最终会变成NULL,最后跳出循环;
}
}
}
if(v!=this->numVertices)//如果这个待删除的下标不等于 最后那个顶点的话 ,因为顶点 调动 位置,所以需要改变 链中顶点下标名字
for(int i = 0 ; i < this->numVertices;i++)
{ Edge_Vertices<T,E> *temp;
temp=this->NodeTable[i].next;
while(temp)
{
if(temp)
if(temp->dest==this->numVertices)//就是说,最后的那个顶点要去前面 替换掉 刚才删除的那个顶点的位置 ,因此,下标也要改
{
temp->dest=v;// 循环遍历 出最后顶点的dest 然后用v 替换
break;
}
temp=temp->link;//移动
}
}
}//第一个else 的右括号
return true;//删除顶点成功
}
template<class T , class E>
E Graphlnk<T,E>::getWeight (int v1, int v2)//获得两个点之间的权值
{
if(v1<this->numVertices&&v2<this->numVertices&&v1!=v2)
{
// string a = this->NodeTable[v2].data;
Edge_Vertices<T,E> *temp;
temp=this->NodeTable[v1].next;//从v1这条链找一个点开始
while(temp)//然后循环,直到找到v2
{
if(temp->dest==v2)//找到了直接返回它的权值
return temp->cost;
else
temp=temp->link; //没找到,移动
}
return maxWeight;
}
}
template<class T , class E >
bool Graphlnk<T,E>::insertVertex (const T& vertex)//插入顶点 ,插在之前定义的那个顶点表那里
{
if(this->numVertices<this->maxVertices)//如果图当前的顶点数小于 允许插入的最大顶点数,则可以插入
{
this->NodeTable[this->numVertices++].data=vertex;
}
}
template<typename T, typename E>
bool Graphlnk<T,E>::insertEdge(T in, T out, E cost)//插入边
{ int v1= getVertexPos(in); //这里还是直接是输入定点名,用函数找这个顶点的下标
int v2=getVertexPos(out);
if(v1>-1 && v1<this->numVertices && v2>-1 && v2 < this->numVertices )//这两个下标都在顶点表里
{ //将新边的权值插入边邻接矩阵的第v1行,v2列,利用头插法
Edge_Vertices<T,E> *temp =new Edge_Vertices<T,E>; //生成一个边结点。
temp->dest=v2;// 记录这个点的值
temp->link=this->NodeTable[v1].next;//将它插在 v1 这个顶点的这条链里 ,这里采用头插法 (temp 街上NodeTable[v1]的后面 一大串(当然一开始为空))
//比如这一大串为ABCDE 然后temp 接上去就为 temp->ABCDE;
if(this->withCost==true)//如果需要记录权值
temp->cost=cost;// 记录
this->NodeTable[v1].next =temp;// 吧temp接上去 head ->temp->ABCDE;
if(this->direction==false)//如果是无向图的话,还要从v2那条链 接上 v1
{
Edge_Vertices<T,E> *temp2=new Edge_Vertices<T,E> ;
temp2->dest=v1;
temp2->link=this->NodeTable[v2].next;
if(this->withCost==true)
temp2->cost=cost;//同样的是采用头插法,不再一一赘述
this->NodeTable[v2].next=temp2;
}
this->numEdges++;
return true;
}
else return false; //插入新边失败(不满足if 语句)
}
//构造函数建立邻接表
template <class T, class E>
Graphlnk<T, E>::Graphlnk (int sz,bool direct, bool cost):Graph<T,E>(sz, direct, cost)
{ //创建源点表数组
NodeTable = new Vertex<T, E>[this->maxVertices];//分10个Vertex结点大小 的指针 数组
if (NodeTable == NULL)
{
cerr << "内存分配出错!" << endl; exit(1);
}
for (int i = 0; i < this->maxVertices; i++)
NodeTable[i].next= NULL;//对NodeTable的指针进行初始化
}
//析构函数:删除一个邻接表
template <class T, class E>
Graphlnk<T, E>::~Graphlnk()
{
for (int vertex = 0; vertex < this->numVertices; vertex++ ){
//current指向源点vertex边链表的第1个邻接点
Edge_Vertices<T, E> * current = NodeTable[vertex].next;
while (current != NULL) {//邻接点存在
NodeTable[vertex].next = current->link; //脱链
delete current; //释放边链表的第1个邻接点
// current重新指向边链表的第1个邻接点
current = NodeTable[vertex].next;
}
}
delete []NodeTable; //删除源点表数组
}
//返回序号为 v 的源点第1个邻接点的序号(从0开始),
//若未找到邻接点, 则返回-1
template <class T, class E>
int Graphlnk<T, E>::getFirstNeighbor (int v)
{ if (v != -1) //源点v存在
{ //current指向源点v的边链表第1个邻接点
Edge_Vertices<T, E>* current = NodeTable[v].next;
if (current != NULL)//顶点v的第1个邻接点存在
//返回第1个邻接点的序号
return current ->dest;
}
return -1; //不存在第1个邻接点,返回-1
}
//返回源点v和邻接点w的下1个邻接点的序号,
//若未找到下1个邻接点, 则返回-1
template <class T, class E>
int Graphlnk<T, E>::getNextNeighbor (int v, int w)
{ if (v != -1) { //源顶点 v 存在
Edge_Vertices<T, E>* current = NodeTable[v].next;//终顶点current
while (current != NULL && current->dest != w)
current = current->link; //先找到终顶点 w
if (current != NULL && current->link != NULL)
//返回w的下1个邻接顶点序号
return current->link->dest;
}
return -1; //未找到下1个邻接顶点,返回-1
}
template <class T, class E>
void Graphlnk<T,E>::Enter()
{ int Count,vertexs,Edges;
T e1,e2;
cout<<"图中共有多少个顶点?";
cin>>vertexs;
cout<<"输入图中共 "<<vertexs<<" 个顶点名:";
//输入图中全部顶点名
for(Count=0;Count<vertexs;Count++)
{ cin>>e1;
insertVertex(e1);
}
E weight;
char Answer;
cout<<"图形的边有方向吗(y/n)?";
cin>>Answer;
if(Answer=='y' || Answer=='Y')
this->direction=true;
else
this->direction=false;
cout<<"图中的边带权吗(y/n)?";
cin>>Answer;
if(Answer=='y' || Answer=='Y')
this->withCost=true;
else
this->withCost=false;
cout<<"图中共有多少条边?";
cin>>Edges;
Count=0;
while(Count<Edges)
{
cout<<"输入第 "<<Count+1<<" 条边的2个顶点名和权值:";
cin>>e1>>e2>>weight;
if(insertEdge(e1,e2,weight))
Count++;
else
cout<<"顶点名有误,重新输入这条边!"<<endl;
}
}
// 输出图中所有顶点和边的信息
template <class T, class E>
void Graphlnk<T, E>::Print(void)
{ int row,column;
E weight;
cout<<"图中共有 "<<this->numVertices<<" 个顶点和 "<<this->numEdges<<" 条边:"<<endl;
for(row=0;row<this->numVertices;row++)
{
//按行号取出序号为row的顶点名并输出
cout<<"序号"<<row<<"源点"<<"["<<getValue(row)<<"]"<<"->";
Edge_Vertices<T, E> *temp;
temp=this->NodeTable[row].next;
if(temp)//可能它的下一个顶点直接就是空
{
while(temp->link)
{
cout<<"["<<"邻接点"<<temp->dest<<"]";
if(this->withCost)
cout<<"["<<"权值"<<temp->cost<<"]";
cout<<"[-]->" ;
temp=temp->link;
}
cout<<"["<<"邻接点"<<temp->dest<<"]";
if(this->withCost)
cout<<"["<<"权值"<<temp->cost<<"]";
cout<<"[^]" ;
cout<<endl;
}
else
cout<<"[^]"<<endl;
}
}
int main()
{
Graphlnk<string,double> graph;
graph.Enter();
graph.Print();
// string del;
// cout<<"请输入你想要删除的一个顶点"<<endl;
// cin>>del;
// int index= graph.getVertexPos(del);
// if(graph.removeVertex (index))
// cout<<"删除成功"<<endl;
// else
// cout<<"删除失败";
// graph.Print();
// cout<<"请输入你想要删除那条边的两个顶点"<<endl;
// string one ,two;
// cin>>one>>two;
// int num_one,num_two;
// num_one=graph.getVertexPos(one);
// num_two=graph.getVertexPos(two);
// if(graph.removeEdge(num_one,num_two))
// cout<<"删除成功"<<endl;
// else
// cout<<"删除失败"<<endl;
// graph.Print();
//cout<<"请输入一个顶点来进行深度优先遍历"<<endl;
// string dfs;
// cin>>dfs;
// graph.DFS(dfs);
// cout<<endl;
//cout<<"请输入一个顶点来进行广度优先遍历"<<endl;
//string bfs;
//cin>>bfs;
//graph.BFS(bfs);
//cout<<endl;
//graph.Connected_Component();
string a,b;
cout<<"输入求最短路径的始顶点:";cin>>a;
int v = graph.getVertexPos(a);
cout<<"输入求最短路径的终顶点:";cin>>b;
int w = graph.getVertexPos(b);
graph.Dijkstra(v);
graph.Print(v,w);
//system("PAUSE");
}
运行结果如下:

以上就是C++ Dijkstra算法之求图中任意两顶点的最短路径的详细内容,更多关于C++ 的资料请关注其它相关文章!
以上是 C++ Dijkstra算法之求图中任意两顶点的最短路径 的全部内容, 来源链接: utcz.com/p/247711.html