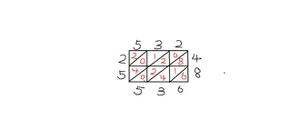
计算矩阵中对角线的总和
我需要在C
++中计算矩阵中两个对角线的总和,对此我已经有解决方案,但是我必须很笨,因为我无法理解它在做什么,所以我想知道是否有另一个版本可以理解。这是完成工作的代码:
cout<<"Jepi rangun e matrices"<<endl; // pra bejme manipulim me matrice katrore ku rreshtat=kolonatcin>>n;
cout<<"Tani jepi elementet e matrices"<<endl; // lexohet matrica
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
cin>>a[i][j];
}
d=0;
s=0; // ketu e keni kushtin si dhe mbledhjen per te dy diagonalet me dy variabla te ndryshme
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(i==j)
d=d+a[i][j];
if(j==n-i+1 || i==n-j+1)
s=s+a[i][j];
}
难以理解的部分是
if(j==n-i+1 || i==n-j+1) s=s+a[i][j];
这是我更改的整个代码,但不适用于辅助对角线:
#include <iostream>using namespace std;
int main()
{
int d=0,s=0; // ketu e keni kushtin si dhe mbledhjen per te dy diagonalet me dy variabla te ndryshme
int i,j,n;
int a[5][5];
cout<<"Jepi rangun e matrices"<<endl; // pra bejme manipulim me matrice katrore ku rreshtat=kolonat
cin>>n;
cout<<"Tani jepi elementet e matrices"<<endl; // lexohet matrica
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
cin>>a[i][j];
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if(i==j)
d+=a[i][j]; //principal diagonal
if(i+j==n-1)
s+=a[i][j];//secondary diagonal
}
}
cout << d << endl;
cout << s << endl;
cin.get();
cin.get();
return 0;
}
回答:
用英语发表评论会很好,但是,您的代码可以(第二循环):
browse all rows browse all cells
if i == j (is in main diagonal):
increase one sum
if i == n - i + 1 (the other diagonal)
increase the second sum
更好,更有效的代码(使用n,而不是n^2)将是:
for( int i = 0; i < n; i++){ d += a[i][i]; // main diagonal
s += a[i][n-i-1]; // second diagonal (you'll maybe need to update index)
}
它穿过对角线(都在一个循环中!),而不会穿过其他项目。
主对角线具有坐标{(1,1), (2,2), ..., (i,i)}(因此i == j)。
次对角线具有坐标(在矩阵3x3中):{(1,3), (2,2),(3,1)}通常为:{(1,n-1+1), (2, n-2+1), ... (i,
n-i+1), .... (n,1)}。但是在C语言中,数组是从0开始索引的,而不是从1开始的索引,因此您将不需要+1(可能)。
所有除有适合条件的二次对角线的项目:i == n - j + 1(再次,由于C中的索引从0
+1变化到-1(i=0,,n=3,j=2,j = n - i - 1))。
您可以在一个循环中完成所有这些操作(上面的代码)。
以上是 计算矩阵中对角线的总和 的全部内容, 来源链接: utcz.com/qa/419438.html