曲线积分问题?
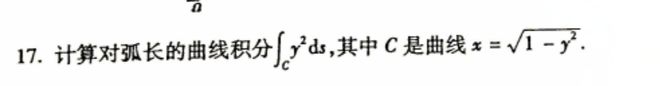
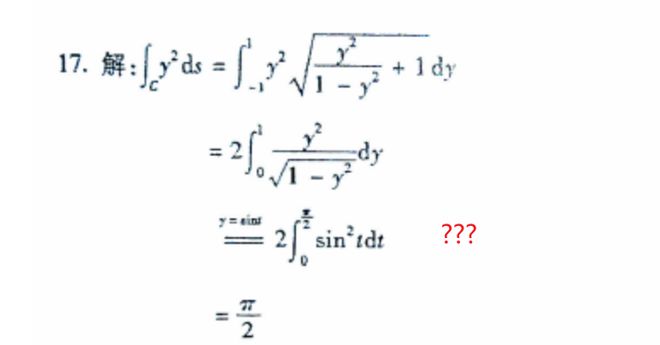
求教大佬 , 第三步是怎么化出来的啊? 我用极坐标代入也没算出这个结果啊。。
回答:
这不是极坐标,就是换元。
y=sin(t), y 在 (0,1) 对应 t 在 (0,pi/2) ,在这个区间,sin(t), cos(t) 都是正的。
直接做 y=sin(t) 的换元:
$$
\int_0^1 \frac{y^2}{\sqrt{1-y^2}}dy \\
=\int_0^{\frac{\pi}{2}}\frac{\sin^2t}{\sqrt{1-\sin^2t}}d\sin t\\
=\int_0^{\frac{\pi}{2}}\frac{\sin^2t}{\sqrt{\cos^2t}}\cos tdt\\
=\int_0^{\frac{\pi}{2}}\sin^2tdt\\
$$
以上是 曲线积分问题? 的全部内容, 来源链接: utcz.com/p/945349.html