循环1M大小二维数组matrix[x][y] ，下面哪种方式更快，并解释原理?

  • Z时代
  • 2024-02-17
  • 分类：IT

循环1M大小二维数组matrixx ，下面哪种方式更快，并解释原理

1、for(int x=0;x<size;x++)
    for(int y=0;y<size;y++)
      matrix[x][y]=x+y;
2、for(int y=0;y<size;y++)
    for(int x=0;x<size;x++)
   matrix[x][y]=x+y;

回答：

第一反应是这是个锤子问题，能有啥差距，一跑还真是差距明显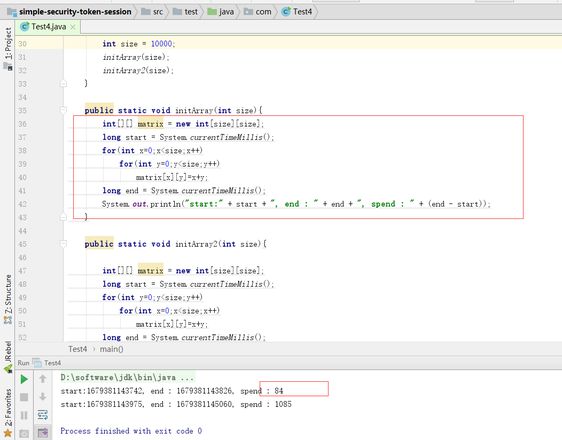

第一反应是字节码有啥骚操作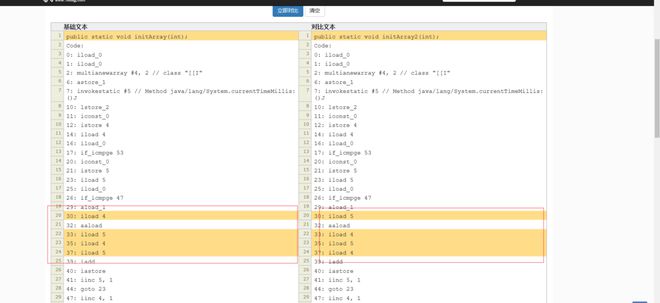
除了取值换了下 确实没啥差异
然后画了个图 - - 第一个数据跳过，如果是取第二个数据的时候，一维数组因为是连续内存，取值上面来说array0应该是是要快于array1的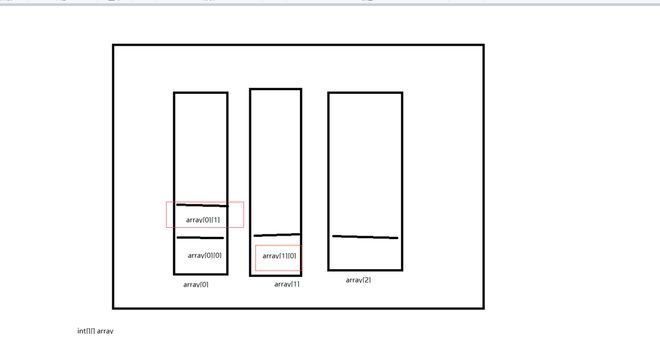

回答：

不管是几维数据他的底层内存结构都是一维的，再加上大部分语言数组是按行存储的，在内存中所以一行的数据后面存储的就是他的下一行，cpu在取数据是会把数据先从内存中取到缓存中(比如L1)如果L1缓存一个缓存行是64byte，再加上现代cpu会对数据进行预取，那么第一种中没16次访存操作都是命中缓存,所以会比第二种快很多，由于1M的大小大概率不会超过CPU的三缓存(比如5950x有64M的三级缓存8M的二级缓存)这两个循环的速度就可以简单的等价于2级缓存和1级缓存速度之间的差距
第二种为啥慢应为他的访存模式导致他每次访存操作都会被映射到不同的缓存行比如
matrix[0][0]
matrix[1][0]
他们属于不同的缓存行而且就算L1缓存有几百K但是由于这种访存模式之前的数据就算加载到了缓存中，也会被后面的数据驱除出缓存也就是说每次从L2中加载了一个缓存行(64个字节)到L1中的只命中了4个字节,而第一种访存方式除了第一次冷缺失其他访存会全部命中L1，前面我们说过matrix[0][0]~matrix[0][16]是连续存储的会被放到同一个缓存行这也是为啥第一种快的原因，下面这张图说明的L1和L2的速度差距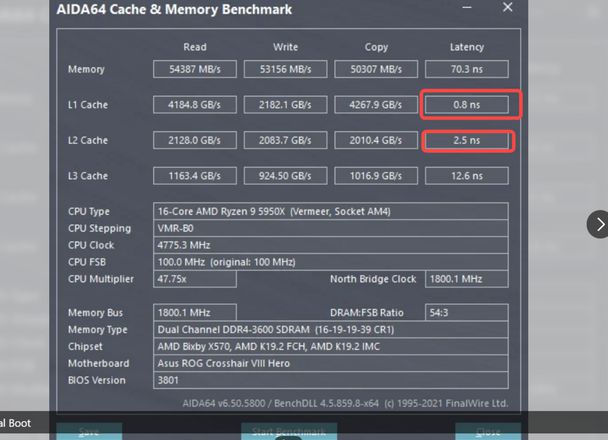

回答：

示例不如这么写

for(int x=0;x<size;x++)
    for(int y=0;y<size;y++)
      matrix[x][y]=x+y; // matrix[y][x]=x+y;

为什么二维数组横向遍历比纵向遍历快？

回答：

不太理解你的问题, 这两个的时间复杂度是一样的O(n^2)

本文参与了SegmentFault 思否面试闯关挑战赛，欢迎正在阅读的你也加入。

回答：

只看时间复杂度上的估计，肯定是一样的

感觉要关注二维数据在java存储的内存中的地址？

回答：

cpu预加载缓存行的问题，二维数组在内存中是一个一维数组的数组结构，横向遍历是一个数组，是一块连续的存储空间，cpu预加载会加载一个缓存行的数据，根据操作系统不同有不同的大小，一般是64字节，横向遍历数据大多都在同一缓存行，在同一个缓存行修改就会很快；纵向遍历的话要加载下一个Y向的值要读取好多暂时用不到的数据，也可能会多次跨缓存行。效率就很慢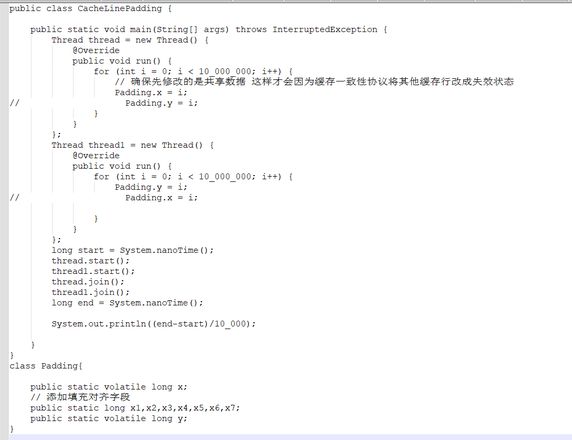

这个例子也是缓存行的一个例子，不添加填充字段和添加填充字段效率也有较大差异

以上是 循环1M大小二维数组matrix[x][y] ，下面哪种方式更快，并解释原理? 的全部内容， 来源链接： utcz.com/p/945233.html

回到顶部