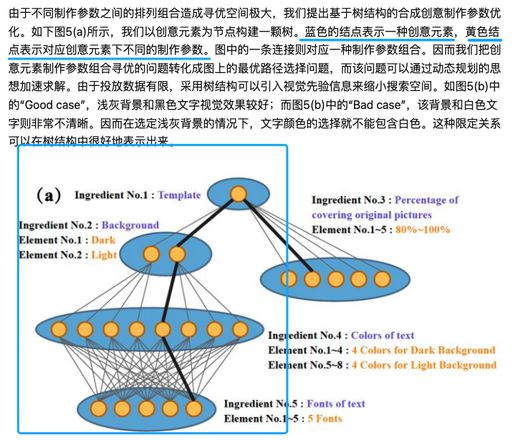
如何把这种结构的每一种结果都遍历出来
回答:
回溯 + BFS/DFS(队列/栈)
首先考虑建图,方便起见,我把结点数量减少为下图
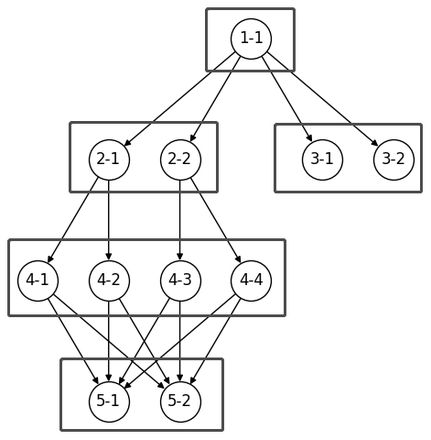
其中每个结点是一个 Element,严格来讲,因为 5-1、5-2 有多个父结点,所以这不是树,而是 DAG(有向无环图)。但是,如果把指向同个 Ingredient 的边合在一起,则是树

由于回溯时,属于同一个 Ingredient 下的 Element 每次只能取一个,所以为了方便区分 Element,可以加一些 Node 对 Element 进行分类
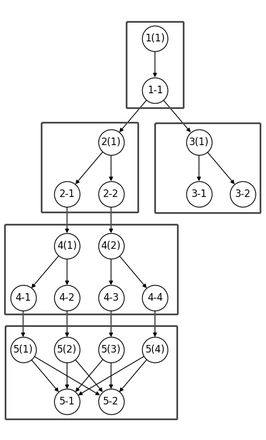
然后就可以开始回溯了,每次取一个 Element,使用 BFS/DFS 遍历指向的所有 Node
因为 Ingredient 序号是层序排列的,所以推荐用 BFS 遍历
回溯 + BFS 核心代码:
void printAllCombinationsInBFSOrder() { System.out.println("BFS Order:");
backtrackBFS(0, 0);
sb.setLength(0);
}
void backtrackBFS(int head, int tail) {
Node uNode = nodeStage[head++]; // 出队
sb.append(uNode.ingredient.no).append('-');
int start = sb.length();
for (Element element : uNode.elements) {
sb.append(element.no);
int _tail = tail;
for (Node vNode : element.nodes)
nodeStage[++_tail] = vNode; // 入队
if (head > _tail) {
System.out.println(sb);
} else {
sb.append(' ');
backtrackBFS(head, _tail);
}
sb.setLength(start);
}
}
BFS Order:1-1 2-1 3-1 4-1 5-1
1-1 2-1 3-1 4-1 5-2
1-1 2-1 3-1 4-2 5-1
1-1 2-1 3-1 4-2 5-2
1-1 2-1 3-2 4-1 5-1
1-1 2-1 3-2 4-1 5-2
1-1 2-1 3-2 4-2 5-1
1-1 2-1 3-2 4-2 5-2
1-1 2-2 3-1 4-3 5-1
1-1 2-2 3-1 4-3 5-2
1-1 2-2 3-1 4-4 5-1
1-1 2-2 3-1 4-4 5-2
1-1 2-2 3-2 4-3 5-1
1-1 2-2 3-2 4-3 5-2
1-1 2-2 3-2 4-4 5-1
1-1 2-2 3-2 4-4 5-2
回溯 + DFS 核心代码:
void printAllCombinationsInDFSOrder() { System.out.println("DFS Order:");
backtrackDFS(0);
sb.setLength(0);
}
void backtrackDFS(int top) {
Node uNode = nodeStage[top--]; // 出栈
sb.append(uNode.ingredient.no).append('-');
int start = sb.length();
for (Element element : uNode.elements) {
sb.append(element.no);
int _top = top + element.nodes.size(), __top = _top;
for (Node vNode : element.nodes)
nodeStage[__top--] = vNode; // 入栈
if (_top < 0) {
System.out.println(sb);
} else {
sb.append(' ');
backtrackDFS(_top);
}
sb.setLength(start);
}
nodeStage[++top] = uNode; // 回栈
}
DFS Order:1-1 2-1 4-1 5-1 3-1
1-1 2-1 4-1 5-1 3-2
1-1 2-1 4-1 5-2 3-1
1-1 2-1 4-1 5-2 3-2
1-1 2-1 4-2 5-1 3-1
1-1 2-1 4-2 5-1 3-2
1-1 2-1 4-2 5-2 3-1
1-1 2-1 4-2 5-2 3-2
1-1 2-2 4-3 5-1 3-1
1-1 2-2 4-3 5-1 3-2
1-1 2-2 4-3 5-2 3-1
1-1 2-2 4-3 5-2 3-2
1-1 2-2 4-4 5-1 3-1
1-1 2-2 4-4 5-1 3-2
1-1 2-2 4-4 5-2 3-1
1-1 2-2 4-4 5-2 3-2
完整代码:
http://java.jsrun.net/HuzKp
以上输出的每一行是制作参数的组合,即包含每种元素中的一个制作参数(黑色加粗的边连接的所有结点)
如果是红色圈起来的路径,那么这个问题可以描述为 从根结点到叶结点的所有路径
回溯即可,还是以这个图为例
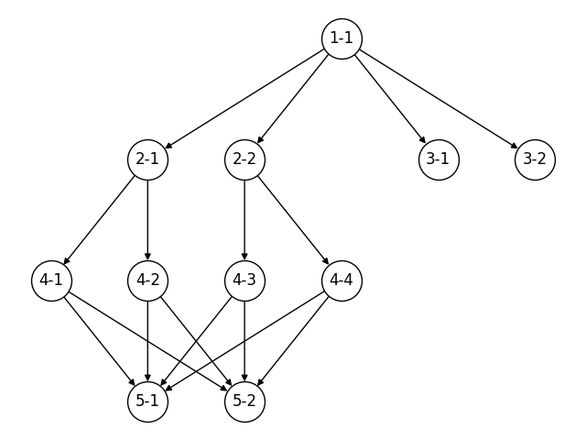
代码:
import java.util.*;public class Traversal {
public static void main(String[] args) {
String[][] input = {
{ "1-1", "2-1", "2-2", "3-1", "3-2" },
{ "2-1", "4-1", "4-2" }, { "2-2", "4-3", "4-4" },
{ "4-1", "5-1", "5-2" }, { "4-2", "5-1", "5-2" },
{ "4-3", "5-1", "5-2" }, { "4-4", "5-1", "5-2" }
};
Map<String, Node> map = new HashMap<>();
for (String[] row : input) {
Node u = map.computeIfAbsent(row[0], Node::new);
for (int i = 1; i < row.length; ++i)
u.children.add(map.computeIfAbsent(row[i], Node::new));
}
backtrack(map.get("1-1"), new StringBuilder());
}
static void backtrack(Node u, StringBuilder sb) {
int start = sb.length();
sb.append(u.no);
if (u.children.size() == 0) {
System.out.println(sb);
} else {
sb.append(' ');
for (Node v : u.children) backtrack(v, sb);
}
sb.setLength(start);
}
}
class Node {
String no;
List<Node> children = new ArrayList<>();
Node(String no) {
this.no = no;
}
}
输出:
1-1 2-1 4-1 5-11-1 2-1 4-1 5-2
1-1 2-1 4-2 5-1
1-1 2-1 4-2 5-2
1-1 2-2 4-3 5-1
1-1 2-2 4-3 5-2
1-1 2-2 4-4 5-1
1-1 2-2 4-4 5-2
1-1 3-1
1-1 3-2
回答:
@OK_a_MI 您好,感谢您的回复。我期待的路径是下图: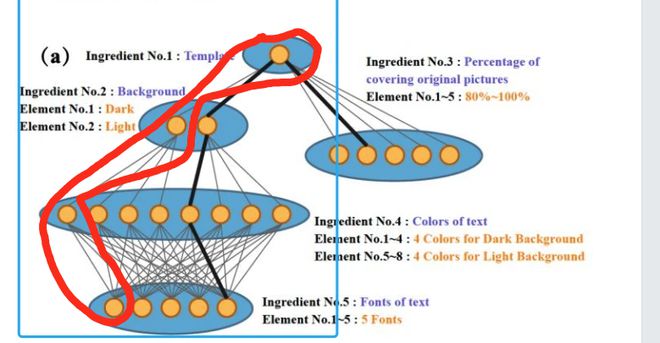
以上是 如何把这种结构的每一种结果都遍历出来 的全部内容, 来源链接: utcz.com/p/944564.html