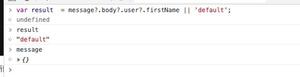
问大家一道我儿子一年级的数学题：求图形里包含多少个矩形

  • Z时代
  • 2024-03-05
  • 分类：IT

这种题数也能数出来，但是有没有规律性的解题思路....因为在程序里硬数是绝对不行的，哈哈
里面包含多少个长方形，（包含正方形）

问大家一道我儿子一年级的数学题：求图形里包含多少个矩形

回答：

问大家一道我儿子一年级的数学题：求图形里包含多少个矩形

1 写程序暴力穷举是能实现的

证明如下：

1.1 已知

  1. 每个点的坐标
  2. 哪两个点之间有连线

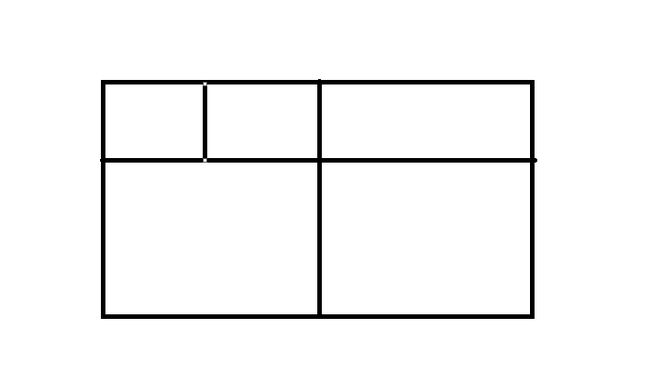
为什么条件2也是必须的，如图，A和D之间有没有连线，H和K之间有没有连线，必须题目给出。

1.2 计算

  1. 穷举所有的线段。题目给的可能是CF，FD两个线段，实际CD也是一个线段。题目给的3个小线段连成一个大线段也是有的：AMEB
  2. 穷举哪4条线段构成一个4边形，判断4个线段是否有且仅有4个公共点即可
  3. 判断上述4边形是否构成矩形，判断4个顶点的横坐标和纵坐标的相等关系即可

如图：

  • 横坐标相等：A和C，B和D
  • 纵坐标相等：A和B，C和D

则ABCD必为矩形

2 小学一年级的暴力破解法

就是硬数。但要有条理。

  • 1个矩形组成的矩形：5个
  • 2个矩形合并成的矩形：4个
  • 3个矩形合并成的矩形：2个
  • 4个矩形合并成的矩形：0个
  • 5个矩形合并成的矩形：1个

总计：12个

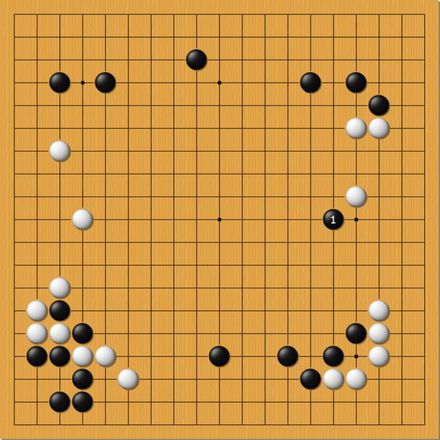
但这个方法只能应对矩形数量少的图形，如果数量多一点，大学生也要数错，各位不信的话，数一下这个围棋棋盘，有多少个矩形（正方形也算矩形）

问大家一道我儿子一年级的数学题：求图形里包含多少个矩形

3 小学三年级的速算法

3.1 删除干扰线速算

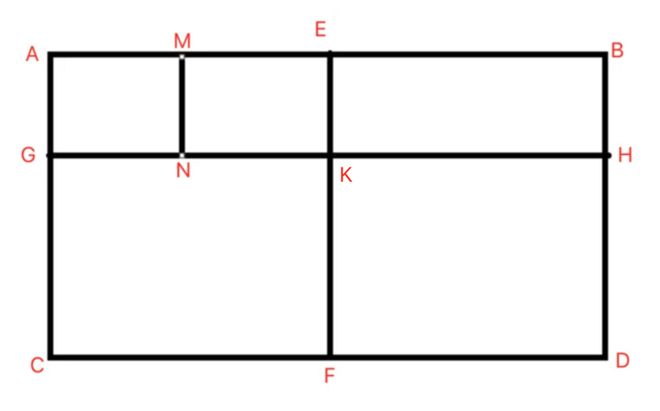
我把线段MN称作干扰线，忽略它，得到这个图：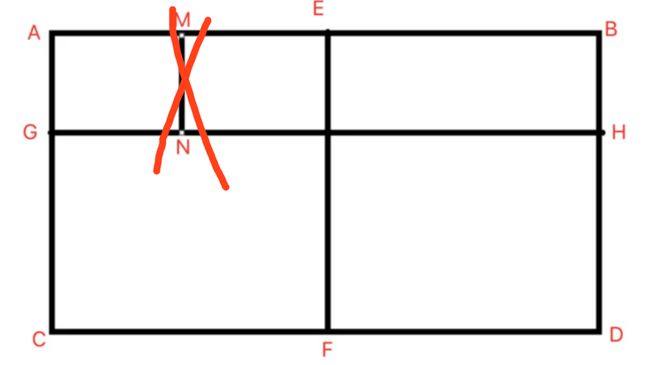
问大家一道我儿子一年级的数学题：求图形里包含多少个矩形

在水平方向，有3条线段，即：AE，EB，AB
在竖直方向，有3条线段，即：AG，GC，AC

则这些线段（以及和他们平行且相等的线段）可以组成3x3=9个矩形

用这个方法，算一下围棋棋盘有多少矩形，是不是快多了？
横向纵向各有18x19/2=171条线段，一共可以组成171x171=29241个矩形

3.2 计算干扰线带来的矩形

3个：AGMN，MNEK，MNBH
再加上9

共计9+3=12个

4 别问我怎么知道的

我是无证小学奥数讲师

回答：

转换成坐标点，遍历求取

var points = [
    [[0, 4], [1, 4], [2, 4], [4, 4]],
    [[0, 2], [1, 2], [2, 2], [4, 2]],
    [[0, 0], [2, 0], [4, 0]]
]
let count = 0
for(let i = 0; i < points.length - 1; i++){
    for(let j = 0; j < points[i].length - 1; j++){
        // 左上角坐标
        let point00 = points[i][j]
        for(let k = j + 1; k < points[i].length; k++){
            // 右上角坐标
            let point10 = points[i][k]
            for(let l = i + 1; l < points.length; l++){
                // 下面两个角坐标
                let point01 = points[l].find(point => point[0] == point00[0])
                let point11 = points[l].find(point => point[0] == point10[0])
                if(point01 && point11){
                    console.log([...point00, ...point11])
                    count++
                }
            }
        }
    }
}
console.log(count)

回答：

规律是有

  1. 单行（列）n 个矩形组成的，有 1 + 2 + ... + n 个，即
    $$\frac{n \times (n + 1)}{2}$$
  2. 规则的多行，因为列行都是上面的算法，所以是
    $$\frac{n \times (n + 1)}{2} \times \frac{m \times (m + 1)}{2}$$

但这个问题有个特殊区域（不规则的），

先算规则的部分是 (1 + 2)(1 + 2) = 9
再算不规则的部分（不用算纵向，只有横向），得先把之前算过的减掉 -(1 + 2) = -3，再加上 1 + 2 + 3 = 6

结果是 9 - 3 + 6 = 12

不出意外应该是算对了。写程序大概也是这个思路，但是要判断特殊的部分。

回答：

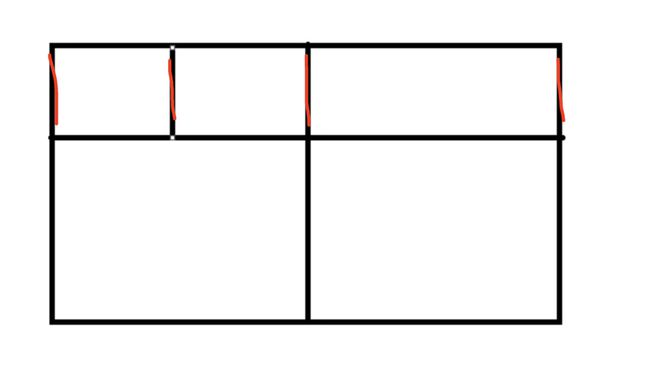
问大家一道我儿子一年级的数学题：求图形里包含多少个矩形
四根红线，任选两根都能组成一个矩形，那么就是C(4,2) 有六个，大概就是这么个规律。然后竖线差不多也是，去掉横线用过的场景

想到另外一个更佳的描述。任意一点A，如果可以按“L”路径到达点B，且AB的连线的斜率是负数，算作一个解。

回答：

提供一个暴力思路

  1. 输入所有点的位置，类似一个二维数组 (x, y)[]
  2. 任取 4 点，进行遍历，判断是否能组成矩形（可以区分正方形、长方形）
  3. 。。。 优化算法

回答：

其实就是个数学建模的问题，你能用数学的方式把你给的那个图形描述出来，那离数的方法也就不远了

回答：

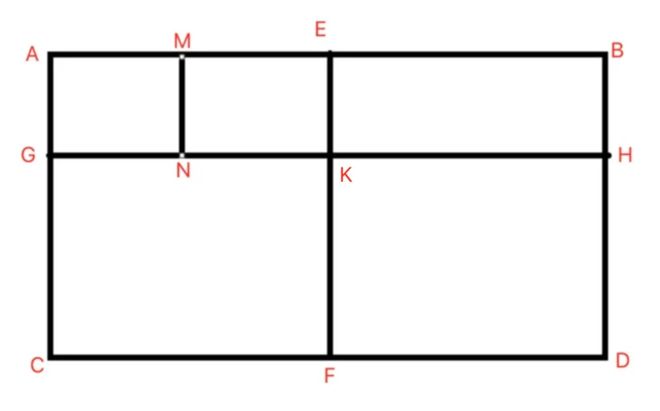
问大家一道我儿子一年级的数学题：求图形里包含多少个矩形

受上面 @冯恒智 这句话启发。【其实就是个数学建模的问题，你能用数学的方式把你给的那个图形描述出来，那离数的方法也就不远了】

我的思路是这样的：图形用水平线和竖直线的点集合数组能表示出来： ["AMEB", "GNKH", "CFD", "AGC", "MN", "EKF", "BHD"]

所以以水平线和竖直线的点集合作为输入，每一条水平线和竖直线的点以个数2进行组合得出所有水平和竖直线段（无斜线），线段集合再以个数4进行组合 得出所有的4边形，然后遍历判断4边形是否是首尾相连的且不在一条直线上的长方形。

// 所有水平线和竖直线
let allLines = ["AMEB", "GNKH", "CFD", "AGC", "MN", "EKF", "BHD"]; 
//存储所有两个点的线段 ["AM","AE","ME",...]
let segmentArr = []; 
//遍历所有水平线和竖直线，收集所有线段。
allLines.forEach((line) => {
    //每条线的点以个数2 进行组合，构成所有线段集合。 
    //generateCombinations 计算组合情况 放在最后。
  let lineSegments = generateCombinations(line.split(""), 2).map((seg) =>
    seg.join("")
  ); 
  segmentArr.push(...lineSegments);
});
 // 所有线段以个数4进行组合，构成所有4边形集合。
let allSegmentCom = generateCombinations(segmentArr, 4).map((item) =>
  item.join("")
);
//每条线的点重新排序，便于后面去重。
let sortAllLines = allLines.map((line) => line.split("").sort().join("")); 
//判断一个4个线段组成的点集合，是否是首尾相连的4边形。   "AMAEABME"
function isRectangle(str) {
  let result = {};
  let len = str.length;
  for (let i = 0; i < len; i++) {
    let dot = str[i];
    if (result[dot]) {
      result[dot]++;
    } else {
      result[dot] = 1;
    }
  }
  let dots = Object.keys(result).sort(); //排序是为了便于去重。
  // 有4个点，每个点出现两次。证明是个首尾相连的4边形。
  if (dots.length == 4 && dots.every((dot) => result[dot] == 2)) {
    let target = dots.join("");
    //target这4个点要排除在在同一条直线里的情况。判断target是否包含在初始条件列出的所有水平和竖直线里。
    if (!sortAllLines.find((item) => item.includes(target))) {
      if (!goodCase.includes(target)) {
        //收集目标
        goodCase.push(target);
      }
    }
  }
}
let goodCase = [];
allSegmentCom.forEach((str) => {
  isRectangle(str);
});
console.log(goodCase);
// ["AGMN","AEGK","ACEF","ABGH","ABCD","EKMN","BHMN","BEHK","BDEF","CFGK","CDGH","DFHK"]
//12个
/**
 工具函数： 计算数组的所有组合情况。
 * Generate all combinations of an array.
 * @param {Array} sourceArray - Array of input elements.
 * @param {number} comboLength - Desired length of combinations.
 * @return {Array} Array of combination arrays.
 */
function generateCombinations(sourceArray, comboLength) {
  const sourceLength = sourceArray.length;
  if (comboLength > sourceLength) return [];
  const combos = []; // Stores valid combinations as they are generated.
  // Accepts a partial combination, an index into sourceArray,
  // and the number of elements required to be added to create a full-length combination.
  // Called recursively to build combinations, adding subsequent elements at each call depth.
  const makeNextCombos = (workingCombo, currentIndex, remainingCount) => {
    const oneAwayFromComboLength = remainingCount == 1;
    // For each element that remaines to be added to the working combination.
    for (
      let sourceIndex = currentIndex;
      sourceIndex < sourceLength;
      sourceIndex++
    ) {
      // Get next (possibly partial) combination.
      const next = [...workingCombo, sourceArray[sourceIndex]];
      if (oneAwayFromComboLength) {
        // Combo of right length found, save it.
        combos.push(next);
      } else {
        // Otherwise go deeper to add more elements to the current partial combination.
        makeNextCombos(next, sourceIndex + 1, remainingCount - 1);
      }
    }
  };
  makeNextCombos([], 0, comboLength);
  return combos;
}

回答：

其实就是有向图的遍历。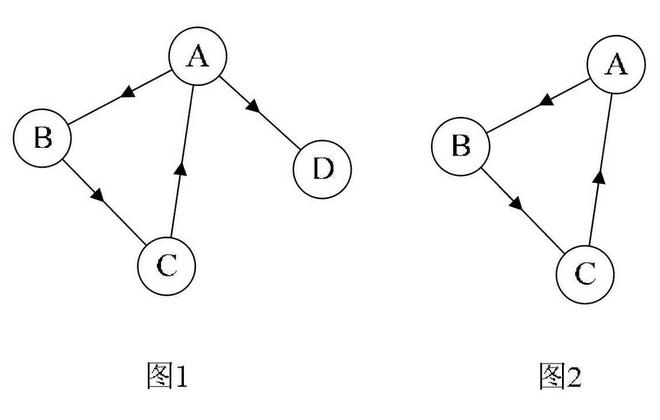
问大家一道我儿子一年级的数学题：求图形里包含多少个矩形

每个顶点遍历后，必须回到这个顶点，找出符合条件的"走法"即可。
边是有向的，上下左右 4方向种。
这个路径必须只能“转向”3次。

回答：

你的标题以及内容没体现出任何问题.
我猜你是想用程序来数长方形是吧.

可以把这些图形转换成坐标,就可以数了

回答：

使用对角线加坐标的方法，应该是最简单的。
任意两个不同的坐标（x1,y1),(x2,y2),若存在坐标(x1,y2)与坐标(x2,y1),则这两个坐标的连线是一个对角线。
遍历循环一下，得到对角线个数，除以2即可。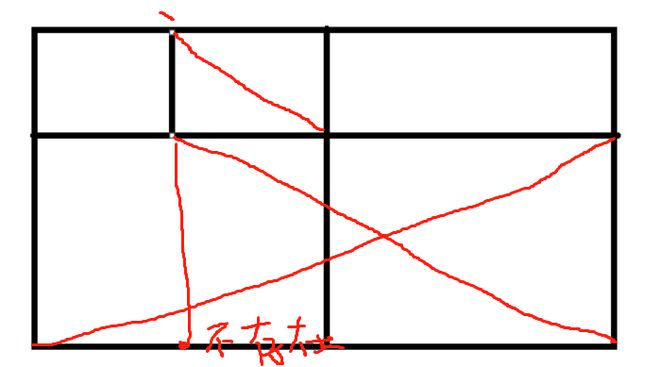
问大家一道我儿子一年级的数学题：求图形里包含多少个矩形

回答：

跟上面的 @张末虎 思路差不多。

遍历找出所有可能的左上、右下两个点，然后再剩余的点找是否存在对应的左下、右上两个点

做一些优化：

  1. 第一个遍历的点作为左上角点，第二个遍历的点必须在第一个点的右下角
  2. 用Set存所有点，后面剩余的左下、右上两个点的复杂度就是O(1)了

这样复杂度就是O(n^2)了

const points = [
  [0, 0],
  [1, 0],
  [2, 0],
  [4, 0],
  [0, 1],
  [1, 1],
  [2, 1],
  [4, 1],
  [0, 3],
  [2, 3],
  [4, 3],
]
/**
 * 
 * @param {Array<number[]>} points 
 */
function calc(points) {
  let count = 0
  // O(1)
  const set = new Set()
  function isExist(point) {
    return set.has(point.join(','))
  }
  points.forEach(([x, y]) => {
    set.add(`${x},${y}`)
  })
  for (let i = 0; i < points.length - 1; i++) {
    // 左上角
    const [x0, y0] = points[i]
    for (let j = i + 1; j < points.length; j++) {
      // 右下角
      const [x1, y1] = points[j]
      if (x1 > x0 && y1 > y0) {
        // 查找左下，右上是否有
        if (isExist([x0, y1]) && isExist([x1, y0])) {
          count++
        }
      }
    }
  }
  return count
}
console.log(calc(points))

回答：

我尝试了用点转换为二维数组，一对，有的边长，有的边段，不正确，所以只能考虑用边
[ [1,1,1,1],
[1,1,1,1],
[1,0,1,1],
[1,1,1,1],]
用边，发现有的边多，有的边少
[ [1,1,1],
[1,1,1],
[1,1,1],]
换！
我把矩形转为点坐标给大家画出来了，大家试试
[[1,1,1,1,1,1,1],
[1,0,1,0,1,0,1],
[1,1,1,1,1,1,1],
[1,0,0,0,1,0,1],
[1,1,1,1,1,1,1]]
我觉得这个从图到图应该也是问题的一部分，所以我把图画出来了供大家验证，对了我挺支持两个点确定一个矩形的方法。

以上是 问大家一道我儿子一年级的数学题：求图形里包含多少个矩形 的全部内容， 来源链接： utcz.com/p/937371.html

回到顶部