C语言实现统计100以内所有素数的个数
本人C语言萌新,最近工作中频频出现C语言小错误,遂决定使用笨方法提高我的C语言水平,坚持每天一个C语言小练习,养成C语言手感,从此让编程成为习惯。
题目描述
统计100以内所有素数的个数
分析
素数(prime number)又称质数,在大于1的自然数中,除了1和它本身以外不再有其他因数的数称为质数,2是最小的素数。
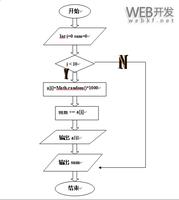
代码实现
#include <stdio.h>
#define INTEGER_RANGE 100 //数字范围
int if_prime(int num);
int main()
{
int sum = 0;
/* 2是最小的素数,for循环范围为2-100 */
for(int i = 2; i <= INTEGER_RANGE; i++)
{
if(if_prime(i))
sum++;
}
printf("%d以内的素数个数为:%d\n", INTEGER_RANGE, sum);
return 0;
}
/*
* 判断是否为素数,是则返回1,否返回0
* */
int if_prime(int num)
{
int i = 0;
for(i = 2; i < num; i++)
{
/* 如果该数有存在1以外的其他正因数,则不是素数 */
if(num % i == 0)
return 0;
}
return 1;
}
运行结果

后期完善
这里只对if_prime(num)函数进行完善:
- 增加非法数字的判断,
num小于2直接返回0 - 将循环范围由
2~num-1改成2~sqrt(num)
至于为什么用sqrt,这里借用下别人的解释(比较通俗易懂)
当一个数不是素数的时候,那这数肯定是除了它本身和1外的两个数之积
( a*b = m ),如果设a是小于或者等于b的数,那a肯定是小于等于m的开根,即a <= sqrt( m )。——百度贴吧(C语言吧)
还有一种用法是把num改成num/2,但是当num大于4时,sqrt(num)比num/2小,所以用sqrt(num)的效率比用num/2高。
至于为什么可以用num/2,这里也借用别人的解释(有点难懂)
其实这是数学知识,n不除以2也行,只是运算量更大,其实最少运算量的方法是n开根号。
我证明一下合理性吧。用反证法。
如果一个数是合数,则一定能分解成两个不是1的数相乘,所以能被分解成一个大于等于2的数和一个小于等于n/2相乘。
如果这个数没有一个小于等于n/2的因数,那它一定不是合数,所以它一定是素数,不用再检查后面的数了。这里是小于n/2,是因为如果这个数能被n/2整除,那2一定是它的因数,很容易知道2小于等于n/2,所以在检查n/2之前一定检查过2。证明完成!
n开根号也差不多这样证明。——https://fishc.com.cn/thread-181309-1-1.html
如果你对上面的两种用法都不理解,那记住它们就行了。。。
#include <math.h>
/*
* 判断是否为素数,是则返回1,否返回0(改进版)
* */
int if_prime(int num)
{
if(num < 2)
return 0; //最小的素数为2
int i = 0;
//sqrt():开方函数(一定要写小于等于)
for(i = 2; i <= sqrt(num); i++)
{
/* 如果该数有存在1以外的其他正因数,则不是素数 */
if(num % i == 0)
return 0;
}
return 1;
}
网上参考
原文链接:https://www.runoob.com/cprogramming/c-exercise-example36.html
sqrt()为开方函数,需要加math.h头文件
// Created by www.runoob.com on 15/11/9.
// Copyright © 2015年 菜鸟教程. All rights reserved.
//
#include<stdio.h>
#include<math.h>
int main()
{
int i,j,k,n=0;
for(i=2;i<=100;i++)
{
k=(int)sqrt(i);
for(j=2;j<=k;j++)
if(i%j==0) break;
if(j>k)
{
printf("%d ",i);
n++;
if(n%5==0)
printf("\n");
}
}
return 0;
}
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持。
以上是 C语言实现统计100以内所有素数的个数 的全部内容, 来源链接: utcz.com/p/247791.html