C语言利用栈实现对后缀表达式的求解

Z时代
2024-01-10
分类：IT

本文实例为大家分享了C语言实现对后缀表达式（逆波兰表达式）的求解代码，供大家参考，具体内容如下

逆波兰表达式：

逆波兰表达式又叫后缀表达式。它是由相应的语法树的后序遍历的结果得到的。

例：5 - 8*(6 + 7) + 9 / 4：

其中缀表达式为：5 - 8 * 6 + 7 + 9 / 4

其语法树如下：

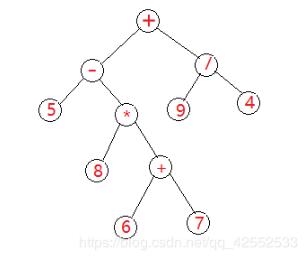
因此根据语法树可以得出他后序遍历（后缀表达式）为：

5 8 6 7 + * - 9 4 / +

这样就实现了中缀表达式到后缀表达式的转换。

同样的也可以得出他的前序遍历（前缀表达式也称波兰表达式）：

　+ - 5 * 8 + 6 7 / 9 4

逆波兰表达式计算实现原理：

1.首先当遇到运算操作数时将其进行push操作；

2.当遇到操作符是将此时的栈pop两次，先取出的栈顶为右操作数；

3.执行此方法到整个数组遍历完。

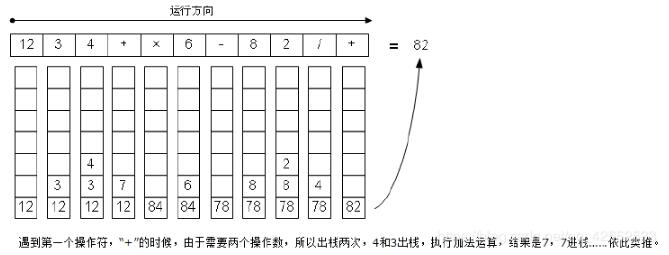
实现算法如下：


void CalFunction(SqStack *S,char str[])
{/*实现浮点型数据后缀表达式的加减乘除*/
 Elemtype number,e,d;
 char arr[MAXBUFFER];
 int i=0,j=0;
 InitStack(S);
 while(str[i]!='\0')
 {
 while(isdigit(str[i])||str[i]=='.') //过滤数字
 {
 arr[j++]=str[i++];
 arr[j]='\0';
 if( j >= MAXBUFFER )
 {
 printf("输入单个数据过大！\n");
 return ;
 }
 if(str[i]==' ')
 {
 number=atof(arr); //利用atof函数将数字字符串转化为double型数据
 PushStack(S,number); //将转换的数进行压栈
 j=0;   //这里不要忘记将j重新初始化进行下个数据的转化
 break;
 }
 }
 /*如果遇到操作运算符则，弹出两个数据进行运算，然后将得出的结果重新入栈*/
 switch(str[i])
 {
 case '+':
 PopStack(S,&e);
 PopStack(S,&d);
 PushStack(S,d+e);
 break;
 case '-':
 PopStack(S,&e);
 PopStack(S,&d);
 PushStack(S,d-e);
 break;
 case '*':
 PopStack(S,&e);
 PopStack(S,&d);
 PushStack(S,d*e);
 break;
 case '/':
 PopStack(S,&e);
 PopStack(S,&d);
 if(e == 0)
 {
 printf("输入出错，分母为零！\n");
 return ;
 }
 PushStack(S,d/e);
 break;
 }
 i++; //继续遍历直到遍历字符串结束
 }
 PopStack(S,&e);
 printf("计算结果为：%lf",e); 
}

完整代码如下：


#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<ctype.h>
#define INITSIZE 20
#define INCREMENT 10
#define MAXBUFFER 10
#define LEN sizeof(Elemtype)
/*栈的动态分配顺序存储结构*/
typedef double Elemtype;
typedef struct{
 Elemtype *base;
 Elemtype *top;
 int StackSize; 
}SqStack;
void InitStack(SqStack *S)
{
 S->base=(Elemtype*)malloc(LEN*INITSIZE);
 assert(S->base != NULL);
 S->top=S->base;
 S->StackSize=INITSIZE;
}
void PushStack(SqStack *S,Elemtype e)
{
 if(S->top - S->base >= S->StackSize)
 {
 S->base=(Elemtype*)realloc(S->base,(S->StackSize+INCREMENT)*LEN);
 assert(S->base !=NULL);
 S->top=S->base+S->StackSize;
 S->StackSize+=INCREMENT;
 }
 *S->top =e;
 S->top++;
}
void PopStack(SqStack *S,Elemtype *e)
{
 *e=*--S->top;
}
void CalFunction(SqStack *S,char str[])
{
 Elemtype number,e,d;
 char arr[MAXBUFFER];
 int i=0,j=0;
 InitStack(S);
 while(str[i]!='\0')
 {
 while(isdigit(str[i])||str[i]=='.') //过滤数字
 {
 arr[j++]=str[i++];
 arr[j]='\0';
 if( j >= MAXBUFFER )
 {
 printf("输入单个数据过大！\n");
 return ;
 }
 if(str[i]==' ')
 {
 number=atof(arr); //利用atof函数将数字字符转化为double型数据
 PushStack(S,number); //将转换的数进行压栈
 j=0;
 break;
 }
 }
 switch(str[i])
 {
 case '+':
 PopStack(S,&e);
 PopStack(S,&d);
 PushStack(S,d+e);
 break;
 case '-':
 PopStack(S,&e);
 PopStack(S,&d);
 PushStack(S,d-e);
 break;
 case '*':
 PopStack(S,&e);
 PopStack(S,&d);
 PushStack(S,d*e);
 break;
 case '/':
 PopStack(S,&e);
 PopStack(S,&d);
 if(e == 0)
 {
 printf("输入出错，分母为零！\n");
 return ;
 }
 PushStack(S,d/e);
 break;
 }
 i++; 
 }
 PopStack(S,&e);
 printf("计算结果为：%lf",e); 
}
int main()
{
 char str[100];
 SqStack S;
 printf("请按逆波兰表达式输入数据,每个数据之间用空格隔开:");
 gets(str);
 CalFunction(&S,str);
 return 0;
}
// 检测用例 5 - (6 + 7) * 8 + 9 / 4
// 输入：5 8 6 7 + * - 9 4 / + # 
// 输出： - 96.750000