java实现八皇后问题示例分享

  • Z时代
  • 2024-01-10
  • 分类：IT

问题描述：将八个皇后放在棋盘上，任何两个皇后都不能互相攻击（即没有任何两个皇后在同一行、同一列或者同一对角线上）如图所示

 

在本文中，对于两道题采用了稍微不同的解决方式，但都使用的是一维数组。6.20中，要求求出一种有效布局，我建立了一个 有八个元素的一位数组，通过随意打乱数组的值，通过值与下标的比较，直至得出一个有效布局；6.22中，要求求出所有有效布局，这里我使用了八进制数，遍历了  从001234567-076543210的所有数字，通过将其转化为八进制字符串，每位与其下标相比较，输出满足条件的布局。下面将对实现原理和方式进行详细介绍。

Part 1 如何判断是否是有效布局

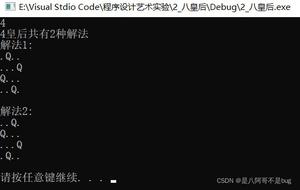
我们将棋盘视为一个8*8矩阵，范围均为0-7。观察左边的图，可以发现，其布局可以用一组数对来表示(从上到下)，即(0, 0), (1, 6), (2, 3), (3, 5), (4, 7), (5, 1), (6, 4), (7， 2)。用一个数组来表示，即 int []list = {0, 6, 3, 5, 7, 1, 4, 2};

显然，这是一个有效布局。下面我们就要考虑一个问题：在有效布局中，下标和其在数组中对应的值，即 i 与 list[i] 有什么关系吗？

这里我们设   list[i] = k; list[j] = q;   (i > j)，它们满足一下两个条件（在纸上画出来更容易明白）：

1、 k != q;

2、 i - j == k - q    或者  i - j == q -k  （由题意得）

为了保证，k != q, 这里声明并初始化 数组list， 使得   list[i] = i。 然后随机打乱数组，然后检查  是否满足条件2

代码如下:
// 创建并初始化数组    int [] list = new int [arrSize];for(int i = 0; i < arrSize; i++)    list[i] = i;// 随机打乱数组public static void randomizeArray(int [] list){    int arrSize = list.length;    int ranIndex;    for(int i = 0; i < arrSize; i++){        ranIndex = (int)(Math.random() * arrSize);        if(ranIndex != i){            int temp = list[i];            list[i] = list[ranIndex];            list[ranIndex] = temp;        }    }}

6.20 的代码主体 如下

代码如下:
// 6.20 游戏：八皇后    public void solveEightQueens(){        int arrSize = 8;        int [] list = new int [arrSize];        for(int i = 0; i < arrSize; i++)            list[i] = i;        int count = 0;        boolean notValid = true;        while(notValid){            count ++;            notValid = false;            randomizeArray(list);

            for(int i = 0; i < arrSize; i++){                for(int j = i + 1; j < arrSize; j++){                    if(j - i == Math.abs(list[j] - list[i])){  // 检查是否满足条件                        notValid = true;                         break;                    }                }                if(notValid) break;            }   // end of outer for loop        }   // end of while        // print the result        int i;        System.out.println("O(∩_∩)O哈哈~, I have tried " + count + " times, and eventually succeed.");        for(i = 0; i < arrSize - 1; i++){            System.out.print("(" + i + ", " + list[i] + "), ");        }        System.out.println("(" + i + ", " + list[i] + ")");    }

Part 2 求出所有的有效布局由于6.22 要求求出所有有效的八皇后布局，随机打乱数组的方法已经不再适用，只好寻求一个可以遍历所有可能的方法。一个最直接的方法是，使用八层 for循环，不过代码量太大，而且脑袋容易晕掉，所以不采用这个方法。

仔细观察Part 1中数组的值，可以发现，它们都在0-7之间，因此使用八进制int数进行遍历可以保证包含每一个排列。由于八位数字各不相同，因此可能的排列有 8! = 40320种，而八进制数总共有  8^8 = 16777216个，因此  可能的比例占  40320/16777216 = 1/416，得到的这40320个排列还要进行检查才能筛选出最终有效的布局。这个方法效率还是有点低，不过暂且还没有想出更高效的。

代码如下:
// 6.22 游戏：多种八皇后问题的解决方案(利用int值递增，然后将其转变为八进制字符串，再进行检查）    public static void solveEightQueensMethod(){        int start = 001234567;  // 八进制        int end = 076543210;   // 八进制        int count = 0;   // 计算有效的布局数        for(int i = start; i < end; i++){            boolean isValid = isValid(i);            if(isValid){                if(++count % 7 == 0)                    System.out.println(Integer.toOctalString(i) + ": " + isValid);                else System.out.print(Integer.toOctalString(i) + ": " + isValid + "  ");            }        }        System.out.println("count = " + count);  // 输出有效的布局数    }// 检查 number 是否是有效布局    public static boolean isValid(int number){        String numOct = Integer.toOctalString(number);        int arrSize = numOct.length();        if(arrSize==7) { // 如果number第一位是0，则生成的字符串只有七个字符            numOct = '0' + numOct;            arrSize ++;        }        for(int i = 1; i < arrSize; i ++){            for(int j = i - 1; j >= 0; j--){                if(numOct.charAt(i) == numOct.charAt(j)) return false;   // 同一列                if(i - j == Math.abs(numOct.charAt(i) - numOct.charAt(j))) return false;  //同一条对角线            }        }        return true;    }

Part 3  延伸：生成组合的问题

去年在一个笔试上，有这样一道题。给定一个序列，输出所有的组合。比如，

“123” 的输出：  1， 2， 3， 12， 13， 21， 23， 31， 32， 123， 132， 213， 231， 312， 321

“abcd”的输出： a, b, c, d, ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc, abc, acb, abd, adb, acd, adc, ..., abcd, ...

在6.22中，求出所有的八皇后布局，使用的方法是是通过 递增 int 型数，再逐个进行检查。上面的问题可以用类似的方法解决。不过效率有点低，如果有更高效的办法，求高手指点

以上是 java实现八皇后问题示例分享 的全部内容， 来源链接： utcz.com/p/207672.html

回到顶部