使用霍夫曼编码进行图像压缩原理和实现细节

Z时代
2024-01-10
分类：IT

编码" title="霍夫曼编码">霍夫曼编码是一种基本的压缩方法, 已被证明在图像和视频压缩标准中有用。在图像上应用霍夫曼编码技术时, 源符号可以是图像的像素强度, 也可以是强度映射函数的输出。

先决条件：霍夫曼编码|文件处理

霍夫曼编码技术的第一步是将输入图像缩小为有序直方图, 其中某个像素强度值的出现概率为

prob_pixel = numpix/totalnum

其中numpix是具有特定强度值的像素的出现次数, 并且总数是输入图像中的像素总数。

让我们拍摄一张8 X 8的图片

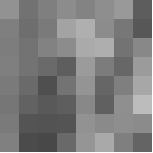
像素强度值为：

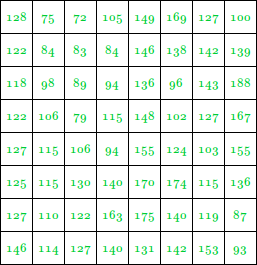
该图像包含46个不同的像素强度值, 因此, 我们将有46个唯一的霍夫曼代码字。

显然, 并非所有像素强度值都可能出现在图像中, 因此不会有非零的出现概率。

从这里开始, 输入图像中的像素强度值将被视为叶节点。

现在, 有两个基本步骤可以构建霍夫曼树：

建立霍夫曼树：

将两个概率最低的叶子节点合并为一个新节点。

用新节点替换两个叶节点, 并根据新的概率值对节点进行排序。

继续步骤(a)和(b), 直到获得概率值为1.0的单个节点。我们称这个节点为根

从根开始回溯, 为每个中间节点分配” 0″或” 1″, 直到到达叶节点

在此示例中, 我们将为左侧的子节点分配” 0″, 为右侧的子节点分配” 1″。

现在, 让我们研究一下实现：

第1步：

将图像读入2D数组(Image)

如果图像是.bmp格式，那么图像可以通过使用此链接中给出的代码读入2D数组（https://github.com/sadimanna/compression/blob/master/readbmp.c）。

int i, j;
char filename[] = "Input_Image.bmp" ;
int data = 0, offset, bpp = 0, width, height;
long bmpsize = 0, bmpdataoff = 0;
int ** image;
int temp = 0;
//Reading the BMP File
FILE * image_file;
image_file = fopen (filename, "rb" );
if (image_file == NULL)
{
     printf ( "Error Opening File!!" );
     exit (1);
}
else 
{
     //Set file position of the 
     //stream to the beginning
     //Contains file signature 
     //or ID "BM"
     offset = 0;
     //Set offset to 2, which 
     //contains size of BMP File
     offset = 2;
     fseek (image_file, offset, SEEK_SET);
     //Getting size of BMP File
     fread (&bmpsize, 4, 1, image_file);
     //Getting offset where the
     //pixel array starts
     //Since the information 
     //is at offset 10 from 
     //the start, as given 
     //in BMP Header
     offset = 10; 
     fseek (image_file, offset, SEEK_SET);
     //Bitmap data offset
     fread (&bmpdataoff, 4, 1, image_file);
     //Getting height and width of the image
     //Width is stored at offset 18 and height
     //at offset 22, each of 4 bytes
     fseek (image_file, 18, SEEK_SET);
     fread (&width, 4, 1, image_file);
     fread (&height, 4, 1, image_file);
     //Number of bits per pixel
     fseek (image_file, 2, SEEK_CUR);
     fread (&bpp, 2, 1, image_file);
     //Setting offset to start of pixel data
     fseek (image_file, bmpdataoff, SEEK_SET);
     //Creating Image array
     image = ( int **) malloc (height * sizeof ( int *));
     for (i = 0; i <height; i++)
     {
         image[i] = ( int *) malloc (width * sizeof ( int ));
     }
     //int image[height][width] 
     //can also be done
     //Number of bytes in the 
     //Image pixel array
     int numbytes = (bmpsize - bmpdataoff) /3; 
     //Reading the BMP File 
     //into Image Array
     for (i = 0; i <height; i++) 
     {
         for (j = 0; j <width; j++)
         {
             fread (&temp, 3, 1, image_file);
             //the Image is a 
             //24-bit BMP Image
             temp = temp & 0x0000FF; 
             image[i][j] = temp;
         }
     }}

创建图像中存在的像素强度值的直方图

//Creating the Histogram
int hist[256];
for (i = 0; i <256; i++)
     hist[i] = 0;
for (i = 0; i <height; i++)
     for (j = 0; j <width; j++)         hist[image[i][j]] += 1;

查找具有非零出现概率的像素强度值的数量

由于像素强度的值在0到255之间, 并且并非所有像素强度值都可以出现在图像中(从直方图以及图像矩阵中可以看出), 因此不会出现非零的出现概率。此步骤的另一个目的是, 具有非零概率值的像素强度值的数量将为我们提供图像中叶节点的数量。

//Finding number of 
//non-zero occurrences
int nodes = 0;
for (i = 0; i <256; i++) 
{
     if (hist[i] != 0)
         nodes += 1;}

计算霍夫曼码字的最大长度

如y.s.b u- mostafa和R.J.McEliece在其论文《Huffman codes中的最大码字长度》中所示，如果

1 / F_ {K + 3}” class=”wp-image-69968″ src=”http://www.srcmini.com/wp-content/uploads/2021/04/quicklatex.com-3543f4c22ad4a4b8f8bf40c395d59832_l3.png”>

, 则在概率最小为p的源的任何有效前缀码中, 最长的码字长度最多为K＆If

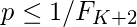
, 存在一个源, 其最小概率为p, 并且具有霍夫曼码, 其最长单词的长度为K。

<img alt="p

, 存在这样一种来源, 对于该来源, 每个最佳代码都具有长度为K的最长字。

这里,

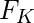
是个

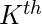
斐波那契数。

Gallager [1] noted that every Huffman tree is efficient, but in fact it is easy to see more

generally that every optimal tree is efficient

斐波那契数列是：0、1、1、2、3、5、8、13、21、34、55、89、144, …

在我们的示例中, 最低概率(p)为0.015625

因此,

1/p = 64

For K = 9, F(K+2) = F(11) = 55F(K+3) = F(12) = 89

因此,

1/F(K+3) <p <1/F(K+2)Hence optimal length of code is K=9

//Calculating max length 
//of Huffman code word
i = 0;
while ((1 /p) <fib(i))
     i++;int maxcodelen = i - 3;

//Function for getting Fibonacci
//numbers defined outside main
int fib( int n)
{
     if (n <= 1)
         return n;
     return fib(n - 1) + fib(n - 2);}

第2步

定义一个结构体，它将包含像素强度值(pix)，它们对应的概率(freq)，指向左(*左)和右(*右)子节点的指针，以及Huffman码字(code)的字符串数组。

这些结构在内部定义main(), 以使用最大的代码长度(maxcodelen)声明代码结构的数组字段pixfreq

//Defining Structures pixfreq
struct pixfreq 
{
     int pix;
     float freq;
     struct pixfreq *left, *right;
     char code[maxcodelen];};

第三步

定义另一个Struct，它将包含像素强度值(pix)，它们对应的概率(freq)和一个额外的字段，该字段将用于存储新生成的节点的位置(arrloc)。

//Defining Structures huffcode
struct huffcode
  {
     int pix, arrloc;
     float freq;};

步骤4

声明结构数组。数组的每个元素对应于霍夫曼树中的一个节点。

//Declaring structs
struct pixfreq* pix_freq;struct huffcode* huffcodes;

为什么要使用两个结构数组？

最初, struct数组pix_freq, 以及struct数组哈夫码将仅包含霍夫曼树中所有叶节点的信息。

结构数组pix_freq将用于存储霍夫曼树和数组的所有节点哈夫码将用作更新(和排序)的树。

记住, 只有哈夫码将在每次迭代中排序, 而不是pix_freq

在每次迭代中, 通过组合频率最低的两个节点而创建的新节点将被附加到pix_freq数组, 也哈夫码数组。

但是数组哈夫码在将新节点添加到节点后, 将根据出现的可能性再次对节点进行排序。

新节点在数组pix_freq中的位置将存储在struct huffcode的arrloc字段中。

当将指针分配给新节点的左子节点和右子节点时，将使用arrloc字段。

步骤4继续…

现在, 如果有ñ叶节点的数量, 整个霍夫曼树中的节点总数将等于2N-1

然后将两个节点合并并替换为新节点父节点, 节点数减少了1在每次迭代中。因此, 长度为节点用于数组哈夫码, 它将用作更新和排序的霍夫曼节点。

int totalnodes = 2 * nodes - 1;
pix_freq = ( struct pixfreq*) malloc ( sizeof ( struct pixfreq) * totalnodes);huffcodes = ( struct huffcode*) malloc ( sizeof ( struct huffcode) * nodes);

第5步

用叶子节点的信息初始化两个数组pix_freq和huffcodes。

j = 0;
int totpix = height * width;
float tempprob;
for (i = 0; i <256; i++) 
{
     if (hist[i] != 0)
     {
         //pixel intensity value
         huffcodes[j].pix = i; 
         pix_freq[j].pix = i;
         //location of the node
         //in the pix_freq array
         huffcodes[j].arrloc = j; 
         //probability of occurrence
         tempprob = ( float )hist[i] /( float )totpix; 
         pix_freq[j].freq = tempprob;
         huffcodes[j].freq = tempprob;
         //Declaring the child of 
         //leaf node as NULL pointer
         pix_freq[j].left = NULL; 
         pix_freq[j].right = NULL;
         //initializing the code
         //word as end of line
         pix_freq[j].code[0] = '\0' ; 
         j++;
     }}

第6步

根据像素强度值出现的概率对huffcodes数组进行排序

请注意, 有必要对哈夫码数组, 但不是pix_freq数组, 因为我们已经将像素值的位置存储在阿罗洛克的领域哈夫码数组。

//Sorting the histogram
struct huffcode temphuff;
//Sorting w.r.t probability 
//of occurrence
for (i = 0; i <nodes; i++)
  {
     for (j = i + 1; j <nodes; j++) 
{
         if (huffcodes[i].freq <huffcodes[j].freq) 
{
             temphuff = huffcodes[i];
             huffcodes[i] = huffcodes[j];
             huffcodes[j] = temphuff;
         }
     }}

步骤7

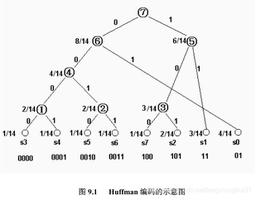
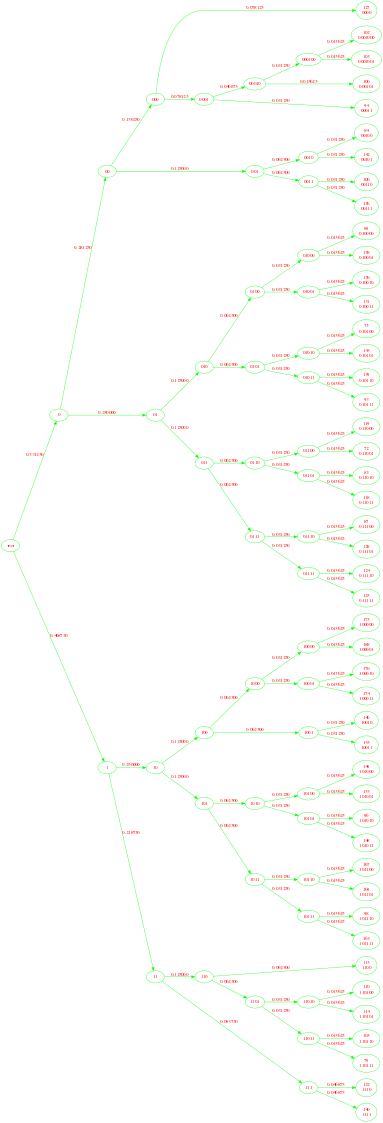
建立霍夫曼树

我们首先将出现概率最低的两个节点组合在一起, 然后用新节点替换两个节点。这个过程一直持续到我们有一个根节点。形成的第一个父节点将存储在索引处节点在数组中pix_freq并且获得的后续父节点将存储在较高的index值中。

//Building Huffman Tree
float sumprob;
int sumpix;
int n = 0, k = 0;
int nextnode = nodes;
//Since total number of 
//nodes in Huffman Tree 
//is 2*nodes-1
while (n <nodes - 1) 
{
     //Adding the lowest 
     //two probabilities
     sumprob = huffcodes[nodes - n - 1].freq + huffcodes[nodes - n - 2].freq;
     sumpix = huffcodes[nodes - n - 1].pix + huffcodes[nodes - n - 2].pix;
     //Appending to the pix_freq Array
     pix_freq[nextnode].pix = sumpix;
     pix_freq[nextnode].freq = sumprob;
     pix_freq[nextnode].left = &pix_freq[huffcodes[nodes - n - 2].arrloc];
     //arrloc points to the location
     //of the child node in the
     //pix_freq array
     pix_freq[nextnode].right = &pix_freq[huffcodes[nodes - n - 1].arrloc];
     pix_freq[nextnode].code[0] = '\0' ;
     //Using sum of the pixel values as 
     //new representation for the new node
     //since unlike strings, we cannot 
     //concatenate because the pixel values 
     //are stored as integers. However, if we
     //store the pixel values as strings
     //we can use the concatenated string as 
     //a representation of the new node.
     i = 0;
     //Sorting and Updating the huffcodes 
     //array simultaneously New position
     //of the combined node
     while (sumprob <= huffcodes[i].freq)
         i++;
     //Inserting the new node in
     //the huffcodes array
     for (k = nnz; k>= 0; k--) 
     {
         if (k == i)
         {
             huffcodes[k].pix = sumpix;
             huffcodes[k].freq = sumprob;
             huffcodes[k].arrloc = nextnode;
         }
         else if (k> i)
             //Shifting the nodes below
             //the new node by 1
             //For inserting the new node 
             //at the updated position k
             huffcodes[k] = huffcodes[k - 1];
     }
     n += 1;
     nextnode += 1;}

此代码如何工作？

我们来看一个例子：

原来

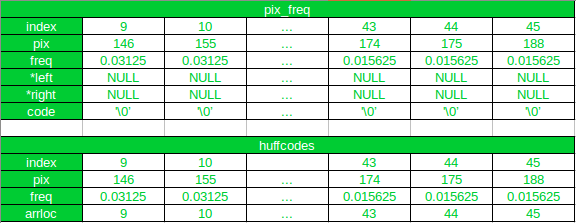
第一次迭代后

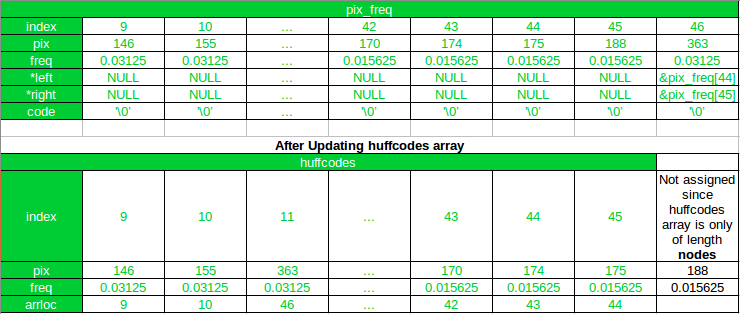
如你所见, 在第一次迭代之后, 新节点已添加到pix_freq数组, 它的索引是46。哈夫码排序后, 新节点已添加到其新位置, 并且阿罗洛克指向中新节点的索引pix_freq数组。此外, 请注意, 在新节点(索引11)之后的所有数组元素哈夫码数组已移位1, 像素值188的数组元素将排除在更新的数组中。

现在，在下一个(第2)迭代中，170和174将被合并，因为175和188已经被合并了。

变量节点和n的最低两个节点的索引为

left_child_index=(nodes-n-2)

和

right_child_index=(nodes-n-1)

在第二次迭代中, n的值为1(因为n从0开始)。

对于值为170的节点

left_child_index=46-1-2=43

对于值为174的节点

right_child_index=46-1-1=44

因此, 即使175仍然是更新数组的最后一个元素, 也会将其排除在外。

此代码中要注意的另一件事是, 如果在任何后续迭代中, 在第一次迭代中形成的新节点是另一个新节点的子节点, 则可以使用以下命令访问在第一次迭代中获得的指向新节点的指针的阿罗洛克存储在哈夫码数组, 如本行代码所示

pix_freq[nextnode].right = &pix_freq[huffcodes[nodes - n - 1].arrloc];

步骤8

从根回溯到叶节点以分配代码字

从根开始, 我们将” 0″分配给左子节点, 将” 1″分配给右子节点。

现在, 由于我们将新形成的节点附加到数组中pix_freq, 因此可以预期根将是数组在索引处的最后一个元素totalnodes-1.

因此, 我们从最后一个索引开始, 遍历数组, 将代码字分配给左右子节点, 直到到达在索引处形成的第一个父节点节点。我们不对叶节点进行迭代, 因为这些节点的左, 右子节点均具有NULL指针。

//Assigning Code through backtracking
char left = '0' ;
char right = '1' ;
int index;
for (i = totalnodes - 1; i>= nodes; i--) {
     if (pix_freq[i].left != NULL) {
         strconcat(pix_freq[i].left->code, pix_freq[i].code, left);
     }
     if (pix_freq[i].right != NULL) {
         strconcat(pix_freq[i].right->code, pix_freq[i].code, right);
     }}

void strconcat( char * str, char * parentcode, char add)
{
     int i = 0;
     while (*(parentcode + i) != '\0' ) {
         *(str + i) = *(parentcode + i);
         i++;
     }
     str[i] = add;
     str[i + 1] = '\0' ;}

最后一步

编码图像

//Encode the Image
int pix_val;
//Writing the Huffman encoded
// Image into a text file
FILE * imagehuff = fopen ( "encoded_image.txt" , "wb" );
for (r = 0; r <height; r++)
     for (c = 0; c <width; c++) {
         pix_val = image[r];
         for (i = 0; i <nodes; i++)
             if (pix_val == pix_freq[i].pix)
                 fprintf (imagehuff, "%s" , pix_freq[i].code);
     }
fclose (imagehuff);
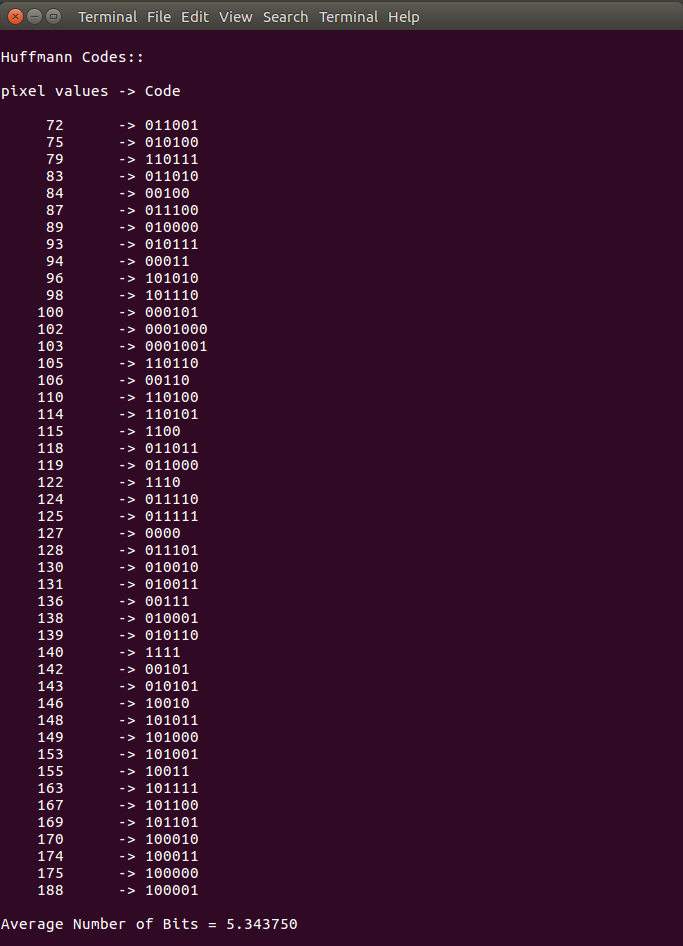
//Printing Huffman Codes
printf ( "Huffmann Codes::\n\n" );
printf ( "pixel values ->   Code\n\n" );
for (i = 0; i <nodes; i++) {
     if (snprintf(NULL, 0, "%d" , pix_freq[i].pix) == 2)
         printf ( "     %d      -> %s\n" , pix_freq[i].pix, pix_freq[i].code);
     else
         printf ( "    %d      -> %s\n" , pix_freq[i].pix, pix_freq[i].code);}

另一个需要注意的重要点

表示每个像素所需的平均位数。

//Calculating Average number of bits
float avgbitnum = 0;
for (i = 0; i <nodes; i++)     avgbitnum += pix_freq[i].freq * codelen(pix_freq[i].code);

功能可伦计算代码字的长度OR, 即表示像素所需的位数。

int codelen( char * code)
{
     int l = 0;
     while (*(code + l) != '\0' )
         l++;
     return l;}

对于此特定示例图像

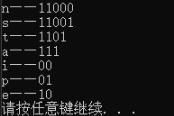
Average number of bits = 5.343750

示例图像的打印结果

pixel values -> Code
         72      -> 011001
         75      -> 010100
         79      -> 110111
         83      -> 011010
         84      -> 00100
         87      -> 011100
         89      -> 010000
         93      -> 010111
         94      -> 00011
         96      -> 101010
         98      -> 101110
        100      -> 000101
        102      -> 0001000
        103      -> 0001001
        105      -> 110110
        106      -> 00110
        110      -> 110100
        114      -> 110101
        115      -> 1100
        118      -> 011011
        119      -> 011000
        122      -> 1110
        124      -> 011110
        125      -> 011111
        127      -> 0000
        128      -> 011101
        130      -> 010010
        131      -> 010011
        136      -> 00111
        138      -> 010001
        139      -> 010110
        140      -> 1111
        142      -> 00101
        143      -> 010101
        146      -> 10010
        148      -> 101011
        149      -> 101000
        153      -> 101001
        155      -> 10011
        163      -> 101111
        167      -> 101100
        169      -> 101101
        170      -> 100010
        174      -> 100011
        175      -> 100000        188      -> 100001

编码图像：

0111010101000110011101101010001011010000000101111 00010001101000100100100100010010101011001101110111001 00000001100111101010010101100001111000110110111110010 10110001000000010110000001100001100001110011011110000 10011001101111111000100101111100010100011110000111000 01101001110101111100000111101100001110010010110101000

0111101001100101101001010111

此编码的图像是342长度, 其中原始图像的总位数为512位。 (每8位64个像素)。

图像压缩码

//C Code for
//Image Compression
#include <stdio.h>
#include <stdlib.h>
//function to calculate word length 
int codelen( char * code)
{
     int l = 0;
     while (*(code + l) != '\0' )
         l++;
     return l;
}
//function to concatenate the words
void strconcat( char * str, char * parentcode, char add)
{
     int i = 0;
     while (*(parentcode + i) != '\0' ) 
     {
         *(str + i) = *(parentcode + i);
         i++;
     }
     if (add != '2' ) 
     {
         str[i] = add;
         str[i + 1] = '\0' ;
     }
     else
         str[i] = '\0' ;
}
//function to find fibonacci number 
int fib( int n)
{
     if (n <= 1)
         return n;
     return fib(n - 1) + fib(n - 2);
}
//Driver code
int main()
{
     int i, j;
     char filename[] = "Input_Image.bmp" ;
     int data = 0, offset, bpp = 0, width, height;
     long bmpsize = 0, bmpdataoff = 0;
     int ** image;
     int temp = 0;
     //Reading the BMP File
     FILE * image_file;
     image_file = fopen (filename, "rb" );
     if (image_file == NULL) 
     {
         printf ( "Error Opening File!!" );
         exit (1);
     }
     else
     {
         //Set file position of the 
         //stream to the beginning
         //Contains file signature 
         //or ID "BM"
         offset = 0; 
         //Set offset to 2, which 
         //contains size of BMP File
         offset = 2;
         fseek (image_file, offset, SEEK_SET);
         //Getting size of BMP File
         fread (&bmpsize, 4, 1, image_file);
         //Getting offset where the
         //pixel array starts
         //Since the information is 
         //at offset 10 from the start, //as given in BMP Header
         offset = 10; 
         fseek (image_file, offset, SEEK_SET);
         //Bitmap data offset
         fread (&bmpdataoff, 4, 1, image_file);
         //Getting height and width of the image
         //Width is stored at offset 18 and 
         //height at offset 22, each of 4 bytes
         fseek (image_file, 18, SEEK_SET);
         fread (&width, 4, 1, image_file);
         fread (&height, 4, 1, image_file);
         //Number of bits per pixel
         fseek (image_file, 2, SEEK_CUR);
         fread (&bpp, 2, 1, image_file);
         //Setting offset to start of pixel data
         fseek (image_file, bmpdataoff, SEEK_SET);
         //Creating Image array
         image = ( int **) malloc (height * sizeof ( int *));
         for (i = 0; i <height; i++)
         {
             image[i] = ( int *) malloc (width * sizeof ( int ));
         }
         //int image[height][width]
         //can also be done
         //Number of bytes in 
         //the Image pixel array
         int numbytes = (bmpsize - bmpdataoff) /3; 
         //Reading the BMP File
         //into Image Array
         for (i = 0; i <height; i++) 
         {
             for (j = 0; j <width; j++) 
             {
                 fread (&temp, 3, 1, image_file);
                 //the Image is a 
                 //24-bit BMP Image
                 temp = temp & 0x0000FF; 
                 image[i][j] = temp;
             }
         }
     }
     //Finding the probability
     //of occurrence
     int hist[256];
     for (i = 0; i <256; i++)
         hist[i] = 0;
     for (i = 0; i <height; i++)
         for (j = 0; j <width; j++)
             hist[image[i][j]] += 1;
     //Finding number of 
     //non-zero occurrences
     int nodes = 0;
     for (i = 0; i <256; i++)
         if (hist[i] != 0)
             nodes += 1;
     //Calculating minimum probability
     float p = 1.0, ptemp;
     for (i = 0; i <256; i++) 
     {
         ptemp = (hist[i] /( float )(height * width));
         if (ptemp> 0 && ptemp <= p)
             p = ptemp;
     }
     //Calculating max length
     //of code word
     i = 0;
     while ((1 /p)> fib(i))
         i++;
     int maxcodelen = i - 3;
     //Defining Structures pixfreq
     struct pixfreq
     {
         int pix, larrloc, rarrloc;
         float freq;
         struct pixfreq *left, *right;
         char code[maxcodelen];
     };
     //Defining Structures
     //huffcode
     struct huffcode 
     {
         int pix, arrloc;
         float freq;
     };
     //Declaring structs
     struct pixfreq* pix_freq;
     struct huffcode* huffcodes;
     int totalnodes = 2 * nodes - 1;
     pix_freq = ( struct pixfreq*) malloc ( sizeof ( struct pixfreq) * totalnodes);
     huffcodes = ( struct huffcode*) malloc ( sizeof ( struct huffcode) * nodes);
     //Initializing
     j = 0;
     int totpix = height * width;
     float tempprob;
     for (i = 0; i <256; i++)
     {
         if (hist[i] != 0) 
         {
             //pixel intensity value
             huffcodes[j].pix = i; 
             pix_freq[j].pix = i;
             //location of the node
             //in the pix_freq array
             huffcodes[j].arrloc = j;
             //probability of occurrence
             tempprob = ( float )hist[i] /( float )totpix; 
             pix_freq[j].freq = tempprob;
             huffcodes[j].freq = tempprob;
             //Declaring the child of leaf 
             //node as NULL pointer
             pix_freq[j].left = NULL; 
             pix_freq[j].right = NULL;
             //initializing the code 
             //word as end of line
             pix_freq[j].code[0] = '\0' ; 
             j++;
         }
     }
     //Sorting the histogram
     struct huffcode temphuff;
     //Sorting w.r.t probability 
     //of occurrence
     for (i = 0; i <nodes; i++)
     {
         for (j = i + 1; j <nodes; j++)
         {
             if (huffcodes[i].freq <huffcodes[j].freq) 
             {
                 temphuff = huffcodes[i];
                 huffcodes[i] = huffcodes[j];
                 huffcodes[j] = temphuff;
             }
         }
     }
     //Building Huffman Tree
     float sumprob;
     int sumpix;
     int n = 0, k = 0;
     int nextnode = nodes;
     //Since total number of 
     //nodes in Huffman Tree 
     //is 2*nodes-1
     while (n <nodes - 1) 
     {
         //Adding the lowest two probabilities
         sumprob = huffcodes[nodes - n - 1].freq + huffcodes[nodes - n - 2].freq;
         sumpix = huffcodes[nodes - n - 1].pix + huffcodes[nodes - n - 2].pix;
         //Appending to the pix_freq Array
         pix_freq[nextnode].pix = sumpix;
         pix_freq[nextnode].freq = sumprob;
         pix_freq[nextnode].left = &pix_freq[huffcodes[nodes - n - 2].arrloc];
         pix_freq[nextnode].right = &pix_freq[huffcodes[nodes - n - 1].arrloc];
         pix_freq[nextnode].code[0] = '\0' ;
         i = 0;
         //Sorting and Updating the 
         //huffcodes array simultaneously
         //New position of the combined node
         while (sumprob <= huffcodes[i].freq)
               i++;
         //Inserting the new node 
         //in the huffcodes array
         for (k = nodes; k>= 0; k--) 
         {
             if (k == i)
             {
                 huffcodes[k].pix = sumpix;
                 huffcodes[k].freq = sumprob;
                 huffcodes[k].arrloc = nextnode;
             }
             else if (k> i)
                 //Shifting the nodes below 
                 //the new node by 1
                 //For inserting the new node
                 //at the updated position k
                 huffcodes[k] = huffcodes[k - 1];
         }
         n += 1;
         nextnode += 1;
     }
     //Assigning Code through
     //backtracking
     char left = '0' ;
     char right = '1' ;
     int index;
     for (i = totalnodes - 1; i>= nodes; i--) 
     {
         if (pix_freq[i].left != NULL)
             strconcat(pix_freq[i].left->code, pix_freq[i].code, left);
         if (pix_freq[i].right != NULL)
             strconcat(pix_freq[i].right->code, pix_freq[i].code, right);
     }
     //Encode the Image
     int pix_val;
     int l;
     //Writing the Huffman encoded
     //Image into a text file
     FILE * imagehuff = fopen ( "encoded_image.txt" , "wb" );
     for (i = 0; i <height; i++)
         for (j = 0; j <width; j++) 
         {
             pix_val = image[i][j];
             for (l = 0; l <nodes; l++)
                 if (pix_val == pix_freq[l].pix)
                     fprintf (imagehuff, "%s" , pix_freq[l].code);
         }
     //Printing Huffman Codes
     printf ( "Huffmann Codes::\n\n" );
     printf ( "pixel values ->   Code\n\n" );
     for (i = 0; i <nodes; i++) {
         if (snprintf(NULL, 0, "%d" , pix_freq[i].pix) == 2)
             printf ( "     %d      -> %s\n" , pix_freq[i].pix, pix_freq[i].code);
         else
             printf ( "    %d      -> %s\n" , pix_freq[i].pix, pix_freq[i].code);
     }
     //Calculating Average Bit Length
     float avgbitnum = 0;
     for (i = 0; i <nodes; i++)
         avgbitnum += pix_freq[i].freq * codelen(pix_freq[i].code);
     printf ( "Average number of bits:: %f" , avgbitnum);}