二十年以来对 RSA 密码系统攻击综述
原文:Twenty Years of Attacks on the RSA Cryptosystem
作者:Dan Boneh@Stanford University(dabo@cs.stanford.edu)
译者:Jing Ling@360ESG A-Team(admin@hackfun.org)
1 介绍
由Ron Rivest,Adi Shamir和Len Adleman发明的RSA密码系统首次在1977年8月的"科学美国人"杂志上发表(译者注:本文于1999年2月在美国数学学会的Notices杂志首次发布)。密码系统最常用于提供隐私保护和确保数字数据的真实性。目前,RSA部署在许多商业系统中。Web服务器和浏览器使用它来保护Web流量,它可以用于保障电子邮件的隐私和真实性,还可以用于保护远程登录会话,同时它也是电子信用卡支付系统的核心。简而言之,RSA常用于需要考虑数字数据安全性的应用中。
自最初发布以来,RSA系统已被许多研究人员分析认为是易受攻击的。尽管二十年的研究出了许多引人入胜的攻击,但其中没有一个攻击是毁灭性的。这些攻击主要说明了不当使用RSA的危险,可见安全地实施RSA确实也是一项非常重要的任务。我们的目标是使用基础数学的知识分析其中的一些攻击,在整个分析过程中,我们遵循标准命名约定,使用Alice和Bob表示希望彼此通信的两个正常通信方,使用Marvin来表示希望窃听或篡改Alice和Bob之间通信的恶意攻击者。
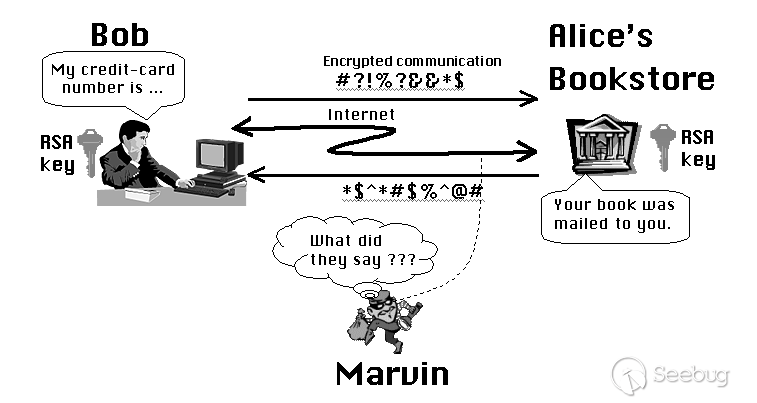
我们首先介绍一下RSA加密的简化版本。令N = pq是比特位长度相同(n/2位)的两个大素数的乘积。常见N的长度大小是n=1024位(即:309个十进制数字),质因子p,q=512位。令e,d为满足ed = 1\ \text{mod}\ \varphi(N)的两个整数,其中\varphi\left( N \right) = (p - 1)(q - 1)是乘法群\mathbb{Z}_{N}^{*}的阶数。我们称N为RSA模数,e为加密指数,d为解密指数。\left\langle N,e \right\rangle为公钥。顾名思义,公钥是公开的,并用于加密消息。\left\langle N,d \right\rangle称为密钥或私钥,一般情况下只有加密消息的接收者知道,私钥能够解密密文。
消息M是一个整数且满足M \in \mathbb{Z}_{N}^{*},要加密M,计算C = M^{e}\ \text{mod}\ N,要解密密文合法接受者计算M = C^{d}\ \text{mod}\ N。(译者注:下面是译者添加的M = C^{d}\ \text{mod}\ N的证明)
欧拉定理:若a,n为正整数,且a,n互素(即\gcd\left( a,n \right) = 1),则a^{\varphi(n)} = 1\ \ \text{mod}\ n。
已知\ 1 = \ ed\ \ \text{mod}\ \varphi(n),m < n,c = m^{e}\ \text{mod}\ n,\gcd\left( m,n \right) = 1,求证m = c^{d}\ \text{mod}\ n。
证明:
等式左边为m
等式右边为c^{d}\ \text{mod}\ n
\because c = m^{e}\ \text{mod}\ n
\therefore c^{d}\ \text{mod}n = {(m^{e}\ \text{mod}\ n)}^{d}\ \ \text{mod}\ n = m^{ed}\ \ \text{mod}\ n
\because 1 = \ ed\ \ \text{mod}\text{\ φ}\left( n \right)
\therefore ed = k\varphi\left( n \right) + 1
\therefore c^{d}\ \text{mod}\ n = m^{ed}\ \ \text{mod}\ n = m^{\text{kφ}\left( n \right) + 1}\ \ \text{mod}\ n = m{(m^{\varphi(n)})}^{k}\ \ \text{mod}\ n
\because\gcd\left( m,n \right) = 1
\therefore m^{\varphi(n)} = 1\ \ \text{mod}\ n
\therefore c^{d}\ \text{mod}\ n = m{(m^{\varphi(n)})}^{k}\ \ \text{mod}\ n = m{(1\ \ \text{mod}\ n)}^{k}\ \ \text{mod}\ n = m{(1)}^{k}\ \ \text{mod}\ n = m\ \ \text{mod}\ n
\because m < n
\therefore m\ \text{mod}\ n = m
\therefore c^{d}\ \text{mod}\ n = m\ \ \text{mod}\ n = m
等式右边等于等式左边,证毕。
定义一个RSA函数x \longmapsto x^{e}\text{modN},如果d已知,很容易使用等式m = c^{d}\ \text{mod}\ n求出x,我们称d为求解函数的陷门。在本次课题研究在没有陷门d的情况下求解RSA函数,更准确的说,给一个三元组\left\langle N,e,C \right\rangle,我们知道在不知道N的因子想计算C模N的e根是非常困难的。因为\mathbb{Z}_{N}^{*}是有限集,因此可以枚举\mathbb{Z}_{N}^{*}的所有元素直到找到M。遗憾的是,这将导致算法具有N阶的运行时间,即其输入大小的指数,其为\mathrm{\log}_{2}N的阶数。我们对运行时间更低的算法感兴趣,即n^{c}的阶数(其中n = \mathrm{\log}_{2}N)或者c是一些小的常数(比如说小于5)。实践表明这些算法通常在所讨论的输入情况表现良好,在整篇论文中,我们将此类算法称为高效算法。
此次课题我们主要研究RSA函数而不是RSA密码系统。笼统地说,随机输入上求解RSA函数的应该是非常困难的,也就是意味着给定\left\langle N,e,C \right\rangle攻击者无法计算出明文M。这还不够,密码系统必须抵御更微妙的攻击。如果给出\left\langle N,e,C \right\rangle,想从M中计算出任何信息应该是非常难的,这被称为语义安全。我们不讨论这些微妙的攻击,但是必须指出的是如上所述的RSA在语义上是不安全的:给定\left\langle N,e,C \right\rangle,可以容易地推导出关于明文M的一些信息(例如,可以容易地从C推导出N上的M的雅可比符号)。通过向加密过程添加随机处理流程,可以保障RSA在语义上的安全性。
RSA函数x \longmapsto x^{e}\text{modN}是一个单向陷门函数,正向它可以很容易地计算,但是(据我们所知)除非在特殊情况下,否则在没有陷门d的情况下不能有效地反向求解的。单向陷门函数可用于数字签名,数字签名可以保障电子文件的真实性和不可否认性。例如,它们用于签署数字支票或电子采购订单。为了使用RSA对消息M \in \mathbb{Z}_{N}^{*}进行签名,Alice使用其私钥\left\langle N,d \right\rangle签名M并获得签名S = M^{d}\ \text{mod}\ N。给定\left\langle M,S \right\rangle之后任何人都可以验证M上的Alice签名通过M = S^{e}\ \text{mod}\ N。因为只有Alice可以生成S,人们可能会认为攻击者无法伪造Alice的签名。然而事情并非如此简单,为了保障签名的安全还需要一些额外的措施。数字签名是RSA的重要应用,此次课题我们也会研究一些针对RSA数字签名的攻击。
RSA密钥对可以这样生成,选取两个随机\frac{n}{2}位素数并将它们相乘以获得N来生成。然后,对于给定的加密指数e < \varphi(N),使用扩展欧几里德算法计算d = e^{- 1}\mathrm{\ \text{mod}}\ \varphi(N)。由于素数集是足够密集的,因此可以通过重复选择随机\frac{n}{2}位整数并使用概率素性测试对每个素数进行素性测试来快速生成随机\frac{n}{2}位素数。
1.1 大数分解
给了RSA公钥\left\langle N,e \right\rangle,首先想到的攻击就是分解模数N,给了N的因子攻击者可以计算得到\varphi(N),从而也可以计算得到解密指数d = e^{- 1}\ \text{mod}\ \varphi(N),我们称这种分解模数的方法为针对RSA的暴力攻击。虽然分解算法已经稳步改进,但是在正确使用RSA情况下,当前的技术水平仍远未对RSA的安全性构成威胁。大整数分解是计算数学之美,不过本文研究主题并不是大整数分解。为完整起见,我们顺便提一下,目前普通数字域筛法是效率最高的分解方法。分解n位整数需要时间为\exp\left( ((c + o(1))n^{\frac{1}{3}}\mathrm{\log}^{\frac{2}{3}}n) \right)其中c < 2,对RSA进行攻击的方法花费时间超过这个范围就那么吸引人了,比如暴力搜索M方法,还有一些RSA发布不久后的旧方法。
我们的目的是研究在不直接分解RSA模数N情况下解密消息的攻击方法,值得注意的是,一些RSA模数的稀疏集,N = pq可以很容易地被分解,举个例子,如果p - 1是乘积的质因子且小于B,那么在小于B^{3}时间内分解N。
如上所述,如果存在有效的因式分解算法,则RSA是不安全的,反之亦然。这是一个由来已久的公开问题:必须要有一个N的因子才能有效地计算e^{th}模N的根数?破解RSA和因式分解一样难吗?我们在下面提出了具体的开放性问题。
开放性问题 1
给定N和e满足\gcd\left( e,\varphi\left( N \right) \right) = 1,定义f_{e,N}函数:\mathbb{Z}_{N}^{*} \rightarrow \mathbb{Z}_{N}^{*},f_{e,N}\left( x \right) = x^{\frac{1}{e}}\mathrm{\ \text{mod}}\ \ N。是否有多项式时间算法A来计算给定N的因子以及对于某个e求得f_{e,N}\left( x \right)的一个谕言?
f\left( x \right)的谕言用于评估在单位时间内任何输入x的函数,最近Boneh和Venkatesan提供的证据表明,在e比较小的情况下,上述问题的答案可能是否定的。换句话说,在e比较小的情况下,可能不存在从分解到破解RSA的多项式时间缩减。他们通过实验表明在某个模型中对小e的问题的肯定答案会产生一个有效的因式分解算法。我们注意到,对开放问题1的肯定回答会引起对RSA的"选择密文攻击"。因此,否定的回答可能才是大家喜闻乐见的。
接下来,我们证明公开私钥d和分解N是等价的。由此可见,对于知道d的任何一方来说,隐藏N的因式分解是没有意义的。
事实1
\left\langle N,e \right\rangle为RSA的公钥,给定私钥d可以有效地分解模数N = pq。相反地,给定N的因式分解,可以有效地算出私钥d。
证明
N的因式分解得到\varphi\left( N \right),因为e已知的,那么可以算出d,反之亦然。我们现在证明给定d可以分解N。给定d,计算k = de - 1。根据d和e的定义我们知道k是\varphi\left( N \right)的倍数。由于\varphi\left( N \right)是偶数,k = 2^{t}r其中r为奇数且t \geq 1。对于每个g \in Z_{N}^{*}都有g^{k} = 1,因此g^{k/2}是单位模N的平方根。根据中国剩余定理,1有四个平方根模N = pq。其中两个平方根是\pm 1,另外两个是\pm x,其中x满足x = 1\mathrm{\ \text{mod}}\ p和x = - 1\mathrm{\ \text{mod}}\ q。用这最后两个平方根中的任意一个,通过计算\mathrm{\gcd}(x - 1,N)来揭示N的因式分解。一个直截了当的论证表明,如果从Z_{N}^{*}中随机选择g,那么序列中的一个元素g^{k/2},g^{k/4},...,g^{k/2^{t}}\ \text{mod}\ N是统一平方根的概率至少为1/2,从而揭示了N的分解,序列中的所有元素可以在时间O(n^{3})内有效地计算,其中n = \log_2N。
2 基本攻击
我们首先描述一些老的基本攻击,这些攻击说明了RSA的公然滥用情况。虽然存在许多这样的攻击,但我们仅举两个例子。
2.1 共模
为了避免为每个用户生成不同的模数N = pq,人们可能希望一劳永逸地固定使用一个N,所有用户都使用相同的N。可信的中央机构可以向用户i提供唯一的一对e_{i},d_{i},用户i从其中生成公钥\left\langle N,e \right\rangle和私钥\left\langle N_{i},e_{i} \right\rangle。
乍一看,这似乎行得通:为Alice准备的密文C = M^{e_{a}}\mathrm{\ \text{mod}}\ \ N无法由Bob解密,因为Bob不知道d_{a}。但是,这是不正确的,由此产生的系统是不安全的。事实上,Bob可以使用他自己的指数e_{b},d_{b}来分解N。一旦N被分解,Bob就可以从她的公钥e_{a}中计算出Alice的私钥d_{a}。Simmons的这一观察结果表明,RSA模不应被一个以上的实体使用。
2.2 盲化
设\left\langle N,d \right\rangle是Bob的私钥,而\left\langle N,e \right\rangle是他相应的公钥。假设攻击者Marvin想要Bob在消息M \in Z_{N}^{*}上签名。当然Bob不是傻瓜,他拒绝签署M。但是Marvin可以尝试以下方法:他随机选择一个r \in Z_{N}^{*}并设M^{'} = r^{e}\text{M}\ \text{mod}\ N。然后他让Bob在随机消息M^{'}上签名。Bob可能愿意在看上去没什么问题的M上签名S^{'},但是回想一下S^{'} = {(M^{'})}^{d}\mathrm{\ \text{mod}}\ \ N,Marvin现在简单地计算S = S^{'}/r\mathrm{\ \text{mod}}\ \ N就得到Bob在初始M上的签名S。
S^{e} = \frac{\left( S^{'} \right)^{e}}{r^{e}} = \frac{\left( M^{'} \right)^{ed}}{r^{e}} \equiv \frac{M^{'}}{r^{e}} = M(\mathrm{\ \text{mod}}\ \ N)
这种称为盲化的技术使Marvin能够在他选择的消息上获得有效的签名,方法是让Bob在随机的"盲化"消息上签名。Bob不知道他实际在签名的是什么消息。由于大多数签名方案在签名之前对消息M应用"单向散列"算法,因此此种攻击倒不是一个严重的问题。尽管我们将盲化描述为一种攻击,但它实际上是实现匿名数字现金所需的一个有用属性(可以用来购买商品的现金,但不会透露购买者的身份)。
3 低私钥指数
为了减少加密时间(或签名生成时间),人们可能希望使用小值d而不是随机d。由于模幂运算需要花费线性时间为\log_2d,所以小d可以使性能提高至少10倍(对于1024位模数而言)。不幸的是,由M.Wiener发现的一种巧妙的攻击表明,一个小的d会导致密码系统完全被攻破。
定理2(M. Wiener)
令N = \text{pq}且q < p < 2q,d < \frac{1}{3}N^{\frac{1}{4}},给定\left\langle N,e \right\rangle且满足ed = 1\ \text{mod}\ \varphi(N),攻击者可以有效计算出d。
证明
证明基于使用连分数的逼近,由于ed = 1\ \text{mod}\ \varphi(N),那么存在一个k满足ed - k\varphi(N) = 1。所以,
\left| \frac{e}{\varphi(N)} - \frac{k}{d} \right| = \frac{1}{d\varphi(N)}
因此,\frac{k}{d}是\frac{e}{\varphi(N)}的逼近,尽管Marvin不知道\varphi(N),但是他可能会使用N去近似\varphi(N)。因为\varphi\left( N \right) = N - p - q + 1(译者注:\varphi\left( N \right) = \left( p - 1 \right)\left( q - 1 \right) = pq - p - q + 1 = N - p - q + 1),p + q - 1 < 3\sqrt{N}(译者注:因为q^{2} < pq = N,所以q < \sqrt{N},所以N - \varphi\left( N \right) = p + q - 1 < 2q + q - 1 < 3q < 3\sqrt{N}),我们有\left| N - \varphi\left( N \right) \right| < 3\sqrt{N}。
使用N替换\varphi(N),我们得到:
\left| \frac{e}{N} - \frac{k}{d} \right| = \left| \frac{ed - kN}{\text{Nd}} \right| = \left| \frac{ed - k\varphi\left( N \right) - kN + k\varphi\left( N \right)}{\text{Nd}} \right|\text{}
= \left| \frac{1 - k\left( N - k\varphi\left( N \right) \right)}{\text{Nd}} \right| \leq \left| \frac{3k\sqrt{N}}{\text{Nd}} \right| = \frac{3k}{d\sqrt{N}}
现在,\text{kφ}\left( N \right) = ed - 1 < ed,因为e < \varphi\left( N \right),我们知道k < d < \frac{1}{3}N^{\frac{1}{4}}(译者注:可以得到3k < 3d < N^{\frac{1}{4}}和dN^{\frac{1}{4}} > 3d^{2})。因此我们得到:
\left| \frac{e}{N} - \frac{k}{d} \right| \leq \frac{1}{dN^{\frac{1}{4}}} < \frac{1}{2d^{2}}(译者注:有的资料写成\frac{1}{3d^{2}})
这是一个经典的逼近关系,分数\frac{k}{d}且d < \varphi(N)在\log_2N约束内非常逼近\frac{e}{N}。实际上,所有类似\frac{k}{d}这样的分数都是\frac{e}{N}的连分数展开的收敛。因此我们首要做的便是计算\frac{e}{N}的连分数的\log N收敛,其中一个连分数就等于\frac{k}{d}。因为ed - k\varphi\left( N \right) = 1,我们有\gcd\left( k,d \right) = 1,因此\frac{k}{d}是一个最简分数。这是可以算出密钥d的线性时间算法。
由于通常N都是1024位,因此d必须至少256位长才能避免这种攻击。这对于诸如"智能卡"之类的低功耗设备来说是不幸的,因为小d就能节省大量能耗。
然而,并不是毫无办法。Wiener提出了许多能够实现快速解密并且不易受其攻击影响的技术:
使用大\mathbf{e}
:假设不是减小e模\varphi\left( N \right),而是使用\left\langle N,e^{'} \right\rangle作为公钥,其中对于某些大t有e^{'} = e + t \cdot \varphi\left( N \right)。
显然,e^{'}可以代替e用于消息加密,当使用大的e值时,上述证明中的k不再小。一个简单的计算表明,如果e^{'} > N^{1.5},那么无论d多小,都无法实施上述攻击。然而,大的e值将导致加密时间的增加。
使用CRT:
另一种方法是使用中国剩余定理(CRT)。假设选择d使得d_{p} = d\mathrm{\ \text{mod}}\ (p - 1)和d_{q} = d\mathrm{\ \text{mod}}\ (q - 1)都很小,比如都是128位。则可以进行如下密文C的快速解密:首先计算M_{p} = C^{d_{p}}\mathrm{\ \text{mod}}\ p和M_{q} = C^{d_{q}}\mathrm{\ \text{mod}}\ q。
然后使用CRT计算满足M = M_{p}\mathrm{\ \text{mod}}\ p和M = M_{q}\mathrm{\ \text{mod}}\ q的唯一值M \in \mathbb{Z}_{N}.
得到的M满足等式M = C_{d}\mathrm{\ \text{mod}}\ \ N。关键点在于虽然d_{p}和d_{q}很小,但是\text{d}\mathrm{\ \text{mod}}\ \varphi(N)的值可以很大,大约在\varphi(N)的数量级上。因此,定理2的攻击不再适用。我们注意到,如果给定了\left\langle N,e \right\rangle,则存在一种攻击能够使攻击者能够在时间O\left( min(\sqrt{d_{p}},\sqrt{d_{q}}) \right)内对N进行因子分解。因此,d_{p}和d_{q}不能太小。
我们不知道这些方法中是否都安全。我们所知道的是,Wiener攻击对它们无效。最近由Boneh和Durfee改进的定理2证明了只要d < N^{0.292},攻击者就可以从\left\langle N,e \right\rangle中有效地算出d。这些结果表明Wiener的界限并不固定。正确的界限可能是d < N^{0.5}。截至撰写本文时,还是一个尚未解决的问题。
开放性问题2
令N = pq,d < N^{0.5},如果Marvin知道\left\langle N,e \right\rangle和ed = 1\mathrm{\ \text{mod}}\ \varphi(N)及e < \varphi(N)关系,他能有效算出d吗?
4 低公钥指数
为了减少加密或签名验证时间,通常会使用一个小的公钥指数e。e的最小可能值为3,但为防止某些攻击,建议使用e = 2^{16} + 1 = 65537。当使用值2^{16} + 1时,签名验证需要17次乘法,而使用随机的e \leq \varphi(N)时则需要大约1000次乘法。与上一节的攻击不同,当使用一个小e时,针对的攻击不只是攻破而已。
4.1 Coppersmith定理
针对RSA低公钥指数最有力的攻击基于Copper-smith的一个定理,Coppersmith定理有很多应用,这里我们只讨论其中的一些应用,证明使用LLL格基约化算法如下。
定理3(Coppersmith)
令N为一个整数,f\mathbb{\in Z}\left\lbrack x \right\rbrack是d次的一元多项式,设X = N^{\frac{1}{d} - \epsilon}其中\epsilon \geq 0,在给定\left\langle N,f \right\rangle之后Marvin能够有效找到所有满足f\left( x_{0} \right) = 0\ \text{mod}\ N的整数\left| x_{0} \right| < X,运行时间由在O(w)维数且w = \mathrm{\min}(\frac{1}{\epsilon},\log_2N)的格上运行LLL算法所需的时间决定。
该定理为有效地求f模N的所有小于X = N^{\frac{1}{d}}的根提供了一种算法,当X越小,算法的运行时间越短。这个定理的强大之处在于它能够找到多项式的小根。当模数为素数时,就目前而言,找不到比使用Coppersmith定理更好的求根算法了,没有理由不使用Coppersmith定理。
我们概述了Coppersmith定理证明背后的主要思想,我们采用由Howgrave-Graham提出的简化方法,给定一个多项式f\left( x \right) = \sum_{}^{}{a_{i}x^{i}\mathbb{\in Z}\left\lbrack x \right\rbrack},定义\left\| h \right\|^{2} = \sum_{i}^{}{\left| a_{i} \right|^{2}},证明依赖于下面的观察。
引理4
令h\left( x \right)\mathbb{\in Z}\left\lbrack x \right\rbrack为d次多项式,X为正整数,假设\left\| h(xX) \right\| < \frac{N}{\sqrt{d}},如果\left| x_{0} \right| < X满足h\left( x_{0} \right) = 0\ \text{mod}\ N,那么h\left( x_{0} \right) = 0成立。
证明 从Schwarz不等式观察到:
\left| {h(x}_{0}) \right| = \left| \sum_{}^{}{a_{i}x_{0}^{i}} \right| = \left| \sum_{}^{}{a_{i}X^{i}}\left( \frac{x_{0}}{X} \right)^{i} \right| \leq \sum_{}^{}\left| a_{i}X^{i}\left( \frac{x_{0}}{X} \right)^{i} \right|
\leq \sum_{}^{}{\left| a_{i}X^{i} \right| \leq}\sqrt{d}\left\| h\left( \text{xX} \right) \right\| < N
因为h\left( x_{0} \right) = 0\ \text{mod}\ N,我们得出结论h\left( x_{0} \right) = 0。
引理指出,如果h是一个低范数多项式,则\text{h}\mathrm{\ \text{mod}}\ \ N的所有小根也是h在整数上的根。引理表明,要找到f\left( x \right)\mathrm{\ \text{mod}}\ \ N的一个小根x_{0},我们需要寻找另一个与f模N有相同根的低范数多项式h \in \mathbb{Z}\left\lbrack x \right\rbrack,这样就能容易找到h在整数上的根x_{0}。为此,我们可以寻找一个多项式g\mathbb{\in Z}\left\lbrack x \right\rbrack,使得h = gf具有低范数,即范数小于N。这相当于寻找具有低范数多项式f,xf,x^{2}f\ldots,x^{r}f的整数线性组合。不过,大多数情况下,并不存在具有足够小的范数的非平凡线性组合。
Coppersmith找到了解决这个问题的窍门:如果f\left( x_{0} \right) = 0\ \text{mod}\ N成立,那么对于任意k则有f\left( x_{0} \right)^{k} = 0\ \text{mod}\ N^{k}。更一般地,定义以下多项式:
g_{u,v}\left( x \right) = N^{m - v}x^{u}f{(x)}^{v}
对于一些预定义的m,则x_{0}是g_{u,v}\left( x \right)模N^{m}的一个根,其中u \geq 0和0 \leq v \leq m。要使用引理4,我们必须找到多项式g_{u,v}\left( x \right)的一个整数线性组合h\left( x \right),使得h(xX)的范数小于N^{m}
(回想一下X是满足X \leq N^{1/d}的x_{0}上界)。由于范数(是N^{m}而不是N)的松弛上界,我们可以证明,对于足够大的m,总是存在一个线性组合h\left( x \right)满足所要求的界。一旦h\left( x \right)被找到,引理4就意味着它有x_{0}作为整数的根,因此,可以很容易地找到x_{0}。
如何有效地找到h\left( x \right)还有待证明,要做到这一点,我们必须说明一些关于\mathbb{Z}^{w}格的基本事实。
设u_{1},\ldots,u_{w} \in \mathbb{Z}^{w}是线性独立的向量。由\left\langle u_{1},\ldots,u_{w} \right\rangle构成的(满秩)格L是u_{1},\ldots,u_{w}的所有整数线性组合的集合。L的行列式定义为w \times w方阵的行列式,它的行列式是向量u_{1},\ldots,u_{w}。
在我们的例子中,我们把多项式g_{u,v}\left( \text{xX} \right)看作向量,并研究了它们所构成的格L。设v = 0,\ldots,m,u = 0,\ldots,d - 1,则格的维数w = d(m + 1)。例如,当f是二次一元多项式且m = 3时,得到的格由以下矩阵的行构成:
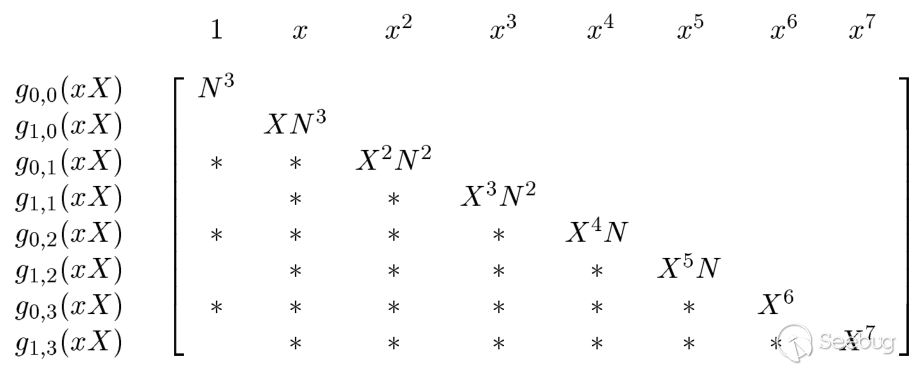
*元对应于我们忽略其值的多项式的系数,所有空元为零。由于矩阵是三角形的,它的行列式是对角线上元素的乘积(如上所示),我们的目标是在这个格中找到短向量。
Hermite的一个经典结论表明:任意维数为w的格L包含一个非零向量v \in L,它的L_{2}范数满足\left\| v \right\| \leq \gamma_{w}{det(L)}^{\frac{1}{w}},其中\gamma_{w}是只依赖于w的常数。Hermite的界可以用来证明,对于足够大的m,我们的格包含需求小于N^{m}的范数向量。问题是我们能否有效地在L中构造长度小于Hermite界的短向量。LLL算法是一种有效的算法,恰好可以做到。
事实5(LLL)
设L是由\left\langle u_{1},\ldots,u_{w} \right\rangle所构成的格。当\left\langle u_{1},\ldots,u_{w} \right\rangle作为输入时,LLL算法输出一个向量v \in L满足:
\left\| v \right\| \leq 2^{\frac{w}{4}}{det(L)}^{\frac{1}{w}}
LLL算法的运行时间是输入长度的四分之一。
LLL算法(以其发明者L. Lovasz、A. Lenstra和H. Lenstra Jr的名字命名)在计算数论和密码学中有许多应用。它在1982年的发现为整数上多项式的因式分解提供了一种有效的算法,更广泛地说,为数环上的多项式的因式分解提供了一种有效的算法。LLL算法经常被用来攻击各种密码系统,例如,许多基于"背包问题"的密码系统都是使用LLL算法破解的。
利用LLL算法,我们可以完成Coppersmith定理的证明。为了保证LLL算法产生的向量满足引理4的界,我们需要满足:
2^{\frac{w}{4}}{det(L)}^{\frac{1}{w}} < \frac{N^{m}}{\sqrt{w}}
其中w = d(m + 1)是L的维数。常规计算表明,对于足够大的m,能满足约束条件。实际上,当X = N^{\frac{1}{d} - \epsilon}时,取m = O(\frac{k}{d})和k = \mathrm{\min}(\frac{1}{\epsilon},\log N)就足够了。因此,运行时间主要由在维数为O(k)的格上运行LLL算法所决定。
一个自然而然的问题,Coppersmith定理能否应用于二元和多元多项式。如果f(x,y) \in \mathbb{Z}_{N}\left\lbrack x,y \right\rbrack有根\left( x_{0},y_{0} \right)且有适当的界\left| x_{0}y_{0} \right|,Marvin能有效地找到\left( x_{0},y_{0} \right)吗?尽管相同的技术似乎适用于某些二元多项式,但目前还是一个有待证明的开放性问题。随着越来越多的结果依赖于Coppersmith定理的二元扩张,所以严密的算法将会非常有用。
开放性问题3
找出Coppersmith定理可以推广到二元多项式的一般条件。
4.2 Hastad广播攻击
作为Coppersmith定理第一个应用,我们对由Hastad提出的旧攻击进行了改进。假设Bob希望将加密消息M发送给多方P_{1},P_{2},\ldots,P_{k}。每一方都有自己的RSA密钥\left\langle N_{i},e_{i} \right\rangle。我们假定M比所有N_{i}都小。Bob为了发送M,天真地使用每个公共密钥对其进行加密,并将第i^{\text{th}}个密文发送给P_{i}。攻击者Marvin可以窃听Bob对外的连接,并收集传输的k个密文。
为了简单起见,假设所有公钥指数e_{i}为3。一个简单的论证表明,当k \geq 3时,Marvin可以计算出M。实际上,Marvin得到C_{1},C_{2},C_{3},其中:
C_{1} = M^{3}\ \text{mod}\ N_{1},C_{2} = M^{3}\ \text{mod}\ N_{2},C_{3} = M^{3}\ \text{mod}\ N_{3}
对于所有的i \neq j,我们可以假设\gcd\left( N_{i},N_{j} \right) = 1,否则Marvin可以因式分解一些N_{i}。因此,将中国剩余定理(CRT)应用于C_{1},C_{2},C_{3},给出的C^{'} \in \mathbb{Z}_{N_{1}N_{2}N_{3}}满足{C^{'} = M}^{3}\ \text{mod}\ N_{1}N_{2}N_{3}。由于M小于所有的N_{i},我们有M^{3} < N_{1}N_{2}N_{3},那么{C^{'} = M}^{3}在整数上成立,因此,Marvin可以通过计算C^{'}的实数立方根来得到M。更一般的情况是,如果所有的公钥指数都等于e,则只要k \geq e,Marvin就可以计算出M。不过这种攻击只有使用较小的e值时才是可行的。
Hastad提出了一种更强的攻击方法。为了抵御Hastad的攻击,考虑一下对上述攻击做一下天真防御。Bob可能在加密之前"填充"消息,而不是广播加密的M。例如,如果M是m位长的,Bob可以将M_{i} = i2^{m} + M发送给P_{i}。由于Marvin获得了不同消息的加密,他无法发起攻击。然而,Hastad证明了这种线性填充是不安全的,事实上,他证明了在加密之前对消息应用任何固定多项式都不能阻止攻击。
假设对于每个参与者P_{1},P_{2},\ldots,P_{k},Bob有一个固定的公用多项式f_{i} \in \mathbb{Z}_{N_{i}}\left\lbrack x \right\rbrack。为了广播消息M,Bob将f_{i}(M)的加密发送给P_{i}。Marvin通过窃听知道了C_{i} = f_{i}{(M)}^{e_{i}}\ \text{mod}\ N_{i},其中i = 1,\ldots,k。Hastad表明,如果有足够的参与方,Marvin可以从所有的密文中计算出明文M。下面的定理是Hastad原始结论的一个更强的版本。
定理6 (Hastad)
设N_{1},\ldots,N_{k}是成对的相对素数,集合N_{\min} = {min}_{i}(N_{i})。设g_{i} \in \mathbb{Z}_{N_{i}}\left\lbrack x \right\rbrack是k个d次多项式。假设存在唯一的M < N_{\min}满足:
g_{i}\left( M \right) = 0\ \text{mod}\ N_{i}(i = 1,\ldots,k)
假设k > d,给定\left\langle N_{i},g_{i} \right\rangle_{i = 1}^{k},我们可以有效地找到的M。
证明
令\overline{N} = N_{1}{\cdots N}_{2},我们假定所有的g_{i}都是一元的。(实际上,对于某些i,g_{i}的首项系数在\mathbb{Z}_{N_{i}}^{*}中是不可逆的,那么N_{i}的因式分解就会显现出来。通过将每个g_{i}乘以x的适当幂,假定它们都有d次。构造多项式:
g\left( x \right) = \sum_{i = 1}^{k}{T_{i}g_{i}(x)},\mathrm{}\mathrm{其中}\mathrm{}T_{i} = \begin{matrix}
1\mathrm{\ \text{mod}}\ \ N_{j}\mathrm{}\mathrm{若}i = j \\
0\mathrm{\ \text{mod}}\ \ N_{j}\mathrm{}\mathrm{若}i = j \\
\end{matrix}
其中T_{i}是整数,被称为中国剩余系数。那么g(x)一定是一元的,因为它首项模了所有的N_{i},且次数为d。此外,我们还知道g(M) = 0\mathrm{\ \text{mod}}\ \overline{N}。定理6现在便可由定理3推导而来,因为M < N_{\min} < {\overline{N}}^{\frac{1}{k}} < {\overline{N}}^{\frac{1}{d}}。
该定理表明,如果提供了足够多的方程,可以有效地求解以相对素数复合模的一元方程组。令g_{i} = f_{i}^{e_{i}} - C_{i},我们可以知道,当参与方数至少为d时,Marvin可以从给定的密文中计算出M,其中d是e_{i}deg(f_{i})在所有i = 1,\ldots,k上的最大值。特别地,如果所有的e_{i}都等于e,并且Bob发送线性相关的消息,那么Marvin只要k > e就可以算出明文。
Hastad的原始定理比上述定理更弱。与d次多项式不同,Hastad定理需要\frac{d(d + 1)}{2}次多项式。Hastad定理的证明类似于上一节中提到的Coppersmith定理证明。由于Hastad定理没有在格中使用g的幂,从而得到了一个较弱的界。
总结这一节,我们注意到,要正确地防御上述广播攻击,必须使用随机填充方法,而不是使用固定填充方法。
4.3 Franklin-Reiter相关消息攻击
当Bob用相同的模数发送与Alice相关的加密消息时,Franklin和Reiter发现了一种聪明的攻击。\left\langle N,e \right\rangle是爱丽丝的公钥,假设M_{1},M_{2} \in Z_{N}^{*}是两个不同的消息,对于某些已知的多项式f \in Z_{N}\left\lbrack x \right\rbrack,M_{1},M_{2}满足M_{1} = f\left( M_{2} \right)\mathrm{\ \text{mod}}\ - N。为了将M_{1}和M_{2}发送给Alice,Bob可能会天真地对消息进行加密,并传输得到的密文C_{1},C_{2}。我们通过证明可以知道,在给定C_{1},C_{2}的情况下,Marvin可以很容易地计算出M_{1},M_{2}。虽然攻击对任意小e都有效,但为了简化证明,我们给出了e = 3的引理。
引理7(FR)
令e = 3,\left\langle N,e \right\rangle为RSA公钥。设M_{1} \neq M_{2} \in Z_{N}^{*}对于b \neq 0的线性多项式f = ax + b \in Z_{N}\left\lbrack x \right\rbrack满足M_{1} = f\left( M_{2} \right)\ \text{mod}\ N。然后,给定\left\langle N,e,C_{1},C_{2},f \right\rangle,Marvin可以在\log N的平方时间内计算出M_{1},M_{2}。
证明
为了保证这部分证明的一般性,我们使用任意e来表示它(而不是限制为e = 3)。由于C_{1} = M_{1}^{e}\mathrm{\ \text{mod}}\ \ N,我们知道M_{2}是多项式g_{1}\left( x \right) = f\left( x \right)^{e} - C_{1} \in Z_{N}\left\lbrack x \right\rbrack的根。同样,M_{2}也是g_{2}\left( x \right) = x^{e} - C_{2} \in Z_{N}\left\lbrack x \right\rbrack的根。线性因子x - M_{2}是两个多项式的除法。因此,Marvin可以使用欧几里德算法来计算g_{1}和g_{2}的最大公约数(Greatest
Common Divisor, GCD)。如果GCD是线性的,则可以找到M_{2}。GCD可以在e和\log N的平方时间内算出。
我们证明了当e = 3时,GCD一定是线性的。多项式x^{3} - C_{2}因子将p和q都模成一个线性因子和一个不可约二次因子(因为\mathrm{\gcd}(e,\varphi\left( N \right)) = 1,所以x^{3} - C_{2}在Z_{N}中只有一个根)。因为g_{2}不能整除g_{1},所以GCD一定是线性的。对于e > 3情况,GCD几乎总是线性的。然而,对于一些罕见的M_{1},M_{2}和f,有可能得到一个非线性的GCD,在这种情况下攻击会失败。
对于e > 3情况,攻击所需时间是e的平方时间。因此,只有在使用小的公钥指数e时才能应用这种攻击。对于大型电子计算机来说,计算GCD的工作令人望而却步。一个有趣的问题(尽管可能很难),为任意的e设计这样的攻击,尤其是能否在\log e的多项式时间中找到上述g_{1}和g_{2}的GCD?
4.4 Coppersmith短填充攻击
Franklin-Reiter的攻击可能看起来有点人为。毕竟,为什么Bob要给Alice发送相关消息的加密呢?Coppersmith加强了攻击,并证明了一个关于填充攻击的重要的结论。
随机填充算法可以通过将一些随机位附加到其中一个端来填充明文M,但是以下攻击指出了这种简单填充的危险。假设Bob向Alice发送了正确填充的M加密。攻击者Marvin拦截密文并阻止其到达目的地。Bob注意到Alice没有回复他的消息,并决定将M重新发送给Alice。他随机填充M并传输生成的密文。Marvin现在有两个密文,对应于使用两种不同随机填充对同一消息的两次加密。以下定理表明,虽然他不知道使用的填充算法,但Marvin仍能够算出明文。
定理8
设\left\langle N,e \right\rangle为RSA公钥,其中N的长度为是n位。令集合m = \left\lbrack n/e^{2} \right\rbrack。设M \in Z_{N}^{*}是长度最长为n - m位的消息。定义M_{1} = 2^{m}M + r_{1}和M_{2} = 2^{m}M + r_{2},其中r_{1}和r_{2}是分别为0 \leq r_{1},r_{2} \geq 2^{m}的整数。如果Marvin知道了\left\langle N,e \right\rangle和M_{1},M_{2}的加密C_{1},C_{2}(但不知道r_{1}或r_{2}),则他可以有效地计算出M。
证明
定义g_{1}\left( x,y \right) = x^{e} - C_{1}和g_{2}\left( x,y \right) = x^{e} - C_{2},我们知道当y = r_{2} - r_{1}时,这些多项式有相同的根M_{1}。换句话说,\Delta = r_{2} - r_{1}是结式h(y) = \text{res}_{x}(g_{1},g_{2}) \in \mathbb{Z}_{N}\left\lbrack y \right\rbrack的根。h的次数最多是e^{2}。此外有\left| \Delta \right| < 2^{m} < N^{\frac{1}{e^{2}}},因此\Delta是h模N的一个小根,而Marvin可以利用Coppersmith定理(定理3)有效地求出这个根。一旦\Delta已知,便可以使用上一节的Franklin-Reiter攻击算出M_{2},从而得到M。
当e = 3时,只要填充长度小于消息长度的\frac{1}{9^{th}},就可以进行攻击。这是一个重要的结论。注意,对于建议值e= 65537,对于标准的模数大小来说,这种攻击是无用的。
4.5 部分密钥泄露攻击
设\left\langle N,d \right\rangle为RSA私钥,假设Marvin通过某种方式知道了d的一部分,比如说四分之一。他能得到d剩下的部分吗?当相应的公钥指数很小时,答案是肯定的,令人惊讶吧。最近,Boneh,Durfee和Frankel证明了只要e < \sqrt{N},就有可能从它的一小部分位算出d的所有部分。可见结论说明了保护整个RSA私钥的重要性。
定理9 (BDF)
设\left\langle N,d \right\rangle为RSA私钥,其中N长度为n位.。给定d的\left\lceil \frac{d}{4} \right\rceil最小有效位,Marvin可以在\text{e}\log_2e的线性时间算出d。
证明依赖于另一个完美精妙的Coppersmith定理。
定理10 (Coppersmith)
设N = PQ是一个n位RSA模。然后,给定p的n/4最小有效位或p的n/4最有效位,可以有效地将N分解。
定理9很容易从定理10推理出来,事实上,根据e和d的定义,存在一个整数k,使得:
ed - k(N - p - q + 1) = 1
由于d < \sqrt{N},我们必有0 < k \leq e。对方程模2^{\frac{n}{4}}进行约化,设q = \frac{N}{p},得到:
\left( ed \right)p - kp\left( N - p + 1 \right) + kN = p(\mathrm{\ \text{mod}}\ 2^{\frac{n}{4}})
由于Marvin知道了d的n/4最小有效位,他知道ed\ \text{mod}\text{}2^{\frac{n}{4}}的值,因此,他得到了一个关于k和p的方程。对于k的每一个e的可能值,Marvin求解p的二次方程,并能得到了p\ \text{mod}\text{}2^{\frac{n}{4}}的一些候选值。对于这些候选值,他运用定理10尝试去分解N。可以证明p\ \text{mod}\text{}2^{\frac{n}{4}}的候选值的总数最多为\text{e}\log_2e,因此,在最多\text{e}\log_2e次尝试之后,N将被分解。
定理9被称为部分密钥泄露攻击,对于更大的e值,只要e < \sqrt{N},也存在类似的攻击,不过,要实现此种攻击的技术有点复杂。有趣的是,基于离散日志的密码系统,如ELGamal公钥系统,似乎不容易受到部分密钥泄漏攻击的影响。事实上,如果给出g^{x}\mathrm{\ \text{mod}}\ p和x的常数部分,则没有已知的多项式时间算法来计算x的其余部分。
为了总结这一节,我们将证明当加密指数e很小时,RSA系统会泄漏相应私钥d一半的最高有效位。要了解这一点,再考虑一个方程ed - k(N - p - q + 1) = 1,其中k是0 < k \leq e的整数。给定k,Marvin可以很容易地计算出:
\widehat{d} = \left\lfloor (kN + 1)/e \right\rfloor
之后:
\left| \widehat{d} - d \right| \leq \frac{k\left( p + q \right)}{e} \leq \frac{3k\sqrt{N}}{e} < 3\sqrt{N}
因此,\widehat{d}是d的很好的近似值。该界表明,对于大多数d,\widehat{d}中一半的最高有效位与d相同。由于k只有e个可能的值,因此Marvin可以构造一个大小e的小集合,使得集合中的一个元素等于d的一半最高有效位的。e = 3的情况特别有趣,在这种情况下,可以知道k = 2,系统完全泄漏了d的一半最高有效位。
5 执行攻击
我们将注意力转向另一类完全不同的攻击。这些攻击不是攻击RSA函数的底层结构,而是专注于RSA的实现。
5.1 时序攻击
想一下存储RSA私钥的智能卡,由于卡是防篡改的,攻击者Marvin可能无法审阅其内容并使其泄露出密钥。然而,Kocher的一个巧妙攻击表明,通过精确测量智能卡执行RSA解密(或签名)所需的时间,可以快速发现私有解密指数d。
我们将解释如何使用"重复平方算法"对一个简单的RSA实现进行攻击。设d = d_{n}d_{n - 1}\ldots d_{0}是d的二进制表示(即d = \sum_{i = 0}^{n}{2^{i}d_{i}},其中d_{i} \in \left\{ 0,1 \right\})。基于C = \prod_{i = 0}^{n}M^{2^{i}d_{i}}\mathrm{\ \text{mod}}\ \ N的观察基础,我们可以知道用重复平方算法来计算C = M^{d}\mathrm{\ \text{mod}}\ \ N最多使用2n次模乘,算法是如下工作的:
令z等于M,C等于1,对于i = 0,\ldots,n,执行以下步骤:
(1)如果d_{i} = 1,令C等于C \bullet z\mathrm{\ \text{mod}}\ \ N,
(2)令z等于z^{2}\mathrm{\ \text{mod}}\ \ N。
最后,C有值为M^{d}\mathrm{\ \text{mod}}\ \ N。
当i = 0,\ldots,n时,变量z遍历M^{2^{i}}\ \text{mod}\ N值的集合,变量C在集合中"收集"适当幂以获得M^{d}\mathrm{\ \text{mod}}\ \ N。
为了发起攻击,Marvin要求智能卡在大量随机消息M_{1},\ldots,M_{k} \in \mathbb{Z}_{N}^{*}上生成签名,并测量每个签名生成所需的时间T_{i}。
攻击从最低有效位开始一次一个地算出d的比特位。我们知道d是奇数,因此d_{0} = 1。考虑第二次迭代。最初z = M^{2}\mathrm{\ \text{mod}}\ \ N且C = M。如果d_{1} = 1,则智能卡会计算乘积C \bullet z = M \bullet M_{i}^{2}\mathrm{\ \text{mod}}\ \ N,否则,它是不会计算的。设t_{i}是智能卡计算M_{i} \bullet M_{i}^{2}\mathrm{\ \text{mod}}\ \ N所花费的时间。由于计算M_{i} \bullet M_{i}^{2}\mathrm{\ \text{mod}}\ \ N的时间取决于M_{i}的值,因此t_{i}彼此不同(简单模约化算法需要不同的时间,取决于所减少的值)。一旦Marvin获得智能卡的物理规格,之后他便会测量得到t_{i}(在发起攻击之前)。
Kocher观察到当d_{1} = 1时,两个集合\left\{ t_{i} \right\}和\left\{ T_{i} \right\}是相关的。例如,如果,对于某些i,t_{i}比预期的要大得多,那么T_{i}也可能大于预期。另一方面,如果d_{1} = 0,则两个集合\left\{ t_{i} \right\}和\left\{ T_{i} \right\}表现为独立的随机变量。通过测量相关性,Marvin可以确定d_{1}是0还是1。继续使用这个方法,他可以很快得到d_{2},d_{3}。注意,当使用低公钥指数e时,上一节的部分密钥泄露攻击表明,使用Kocher的时序攻击,只需要知道d的四分之一的位就行。
有两种方法可以抵御攻击。最简单的是添加适当的延迟,以使模幂运算总是要花费一定的时间。第二种方法是由Rivest提出的基于盲化的方法。在解密M之前,智能卡选择一个随机的r \in \mathbb{Z}_{N}^{*}并计算M^{'} = M \bullet r^{e}\mathrm{\ \text{mod}}\ \ N,然后将d应用于M^{'}上并获得C^{'} = \left( M^{'} \right)^{d}\mathrm{\ \text{mod}}\ \ N,最后,令C = \frac{C^{'}}{r}\text{modN}。通过这种方法,将d应用于Marvin不知道的随机消息M^{'}上,这样的话,Marvin就不能发起攻击了。
Kocher最近在这些线路上发现了另一种叫做功率密码分析的攻击。
Kocher表明,通过在签名生成过程中精确测量智能卡的功耗,Marvin通常可以轻松发现密钥。事实证明,在多精度乘法期间,卡的功耗高于正常值。通过测量高消耗周期的长度,Marvin可以很容易地确定在给定的迭代中卡是执行一次还是两次乘法,从而暴露出d的比特位。
Kocher最近发现了另一种类似的攻击,称为能量分析攻击。Kocher指出通过精确测量智能卡在签名生成过程中的功耗,Marvin通常可以很容易地得到秘密密钥。结果表明,在多精度乘法过程中卡的功耗会高于正常值,通过测量高消耗周期的长度,Marvin可以很容易地确定在给定的迭代中卡是否执行一次或两次乘法,从而得到d的比特位。
5.2 随机故障
RSA的解密和签名的实现经常使用中国剩余定理来加速M^{d}\mathrm{\ \text{mod}}\ \ N的计算,签名者Bob为了替换模N的工作,先计算签名模p和q的结果,然后利用中国剩余定理将结果结合起来。更准确地说,Bob首先计算:
C_{p} = M^{d_{p}}\mathrm{\ \text{mod}}\ p和C_{q} = M^{d_{q}}\mathrm{\ \text{mod}}\ q
其中d_{p} = d\mathrm{\ \text{mod}}\ (p - 1)和d_{q} = d\mathrm{\ \text{mod}}\ (q - 1)。然后,他得到签名C通过令:
C = T_{1}C_{p} + T_{2}C_{q}\left( \mathrm{\ \text{mod}}\ \ N \right)
其中:
T_{1} = \left\{ \frac{1\mathrm{\ \text{mod}}\ p}{0\mathrm{\ \text{mod}}\ q} \right\} 和T_{2} = \left\{ \frac{1\mathrm{\ \text{mod}}\ p}{0\mathrm{\ \text{mod}}\ q} \right\}
与d_{p}和d_{q}两个指数相比,CRT最后一步的运行时间可以忽略不计。注意p和q是N的一半长,然后由于乘法的简单实现需要平方时间,所以模p的乘法速度是模N的4倍,而且,d_{p}是d的一半长,计算M^{d_{p}}\mathrm{\ \text{mod}}\ p的速度是计算M^{d}\mathrm{\ \text{mod}}\ \ N的8倍,因此,整个签名时间减少了四倍,许多实现都使用这种方法来提高性能。
Boneh,DeMillo和Lipton观察到使用CRT方法有内在的危险。假设在生成签名时,Bob的计算机上的一个小故障导致它在一条指令中错误计算。例如,在将寄存器中的值从一个位置复制到另一个位置时,其中一个比特位被翻转了。(故障可能是由环境电磁干扰引起的,也可能是由于罕见的硬件缺陷造成的,比如早期版本的奔腾芯片。)
Marvin得到了无效的签名给定之后可以很容易地对Bob的模数N进行分解。
正如A. K. Lenstra所说,我们发现了一个新的攻击。假设在Bob生成签名时发生单个错误,那么,C_{p}或C_{q}中将有一个被错误地计算。如果说C_{p}是正确的,那么{\widehat{C}}_{q}就会不正确,得到的签名为\widehat{C} = T_{1}C_{p} + T_{2}{\widehat{C}}_{q}。一旦Marvin获取到了\widehat{C},通过计算{\widehat{C}}^{e} \neq M\mathrm{\ \text{mod}}\ \ N,他就知道这是一个错误的签名。然而注意到:
{\widehat{C}}^{e} = M\mathrm{\ \text{mod}}\ p当{\widehat{C}}^{e} \neq M\mathrm{\ \text{mod}}\ q
因此,\mathrm{\gcd}(N,{\widehat{C}}^{e} - M)便是N的一个非平凡因子。
要使攻击奏效,Marvin必须对M有充分的了解。也就是说,我们假设Bob不使用任何随机填充方法,签名前的随机填充可以防御此种攻击,对于Bob来说,一个更简单的防御方法是在将生成的签名发送给全世界之前检查生成的签名。当使用CRT加速方法时,检查是特别重要的。随机故障攻击对许多密码系统都是有害的,许多系统,包括RSA的非CRT实现,都可以使用随机故障进行攻击。不过,这些结论更多的是理论性的。
5.3 Bleichenbacher对PKCS 1的攻击
设N是n位RSA模,M是m位消息,其中m < n。在应用RSA加密之前,一般会通过向其添加随机位,将消息M填充到n位。公钥加密标准1(Public Key Cryptography Standard 1, PKCS 1)的旧版标准就是使用的这种方法。填充后,消息如下所示:
02 随机位 00 M
生成的消息长度为n位,并直接使用RSA加密。包含"02"的初始块长度为16位,从上图可看出已在消息中添加了随机填充。
当运行在Bob的机器上应用程序(例如,Web浏览器)接收到消息时,会对其进行解密,检查初始块,并去掉随机填充。但是,一些应用程序会检查"02"初始块,如果不存在,就会返回一条错误消息,说明"无效的密文"。Bleichenbacher表示这个错误消息可能导致灾难性的后果:攻击者Marvin可以使用错误消息解密他所选择的密文。
假设Marvin截获了一个针对Bob的密文C,并希望对其进行解密。为了发动攻击,Marvin随机挑选了一个r \in \mathbb{Z}_{N}^{*},计算C^{'} = rC\mathrm{\ \text{mod}}\ \ N,并将C^{'}发送到Bob的机器。运行在Bob的机器上的应用程序接收C^{'}并尝试解密它。它要么用错误消息进行响应,要么根本不响应(如果C^{'}的格式正确的话)。因此,Marvin知道C^{'}解密过程中16位最高有效位是否等于02。实际上,Marvin有这样的谕言,对于他选择的任何r,他都可以测试\text{rC}\ \text{mod}\ N解密的16位最高有效位是否等于02。Bleichenbacher证明了这样的谕言足以解密C。
6 结论
对RSA系统进行了20年的研究以来,产生了一些有见地的攻击,但还没有发现破坏性的攻击。到目前为止发现的攻击主要说明了在实现RSA时需要避免的陷阱,目前看来,可以信任正确的RSA密码系统实施来提供数字世界中的安全性。我们将针对RSA的攻击分为四类:(1)利用系统公然误用的基本攻击;(2)低私钥指数攻击,此种攻击非常严重,绝不能使用低私钥指数;(3)低公钥指数攻击;(4)对RSA系统执行时的攻击。这些持续不断的攻击说明,我们对基本数学结构的研究还是不够的。另外,Desmedt和Odlyzko、Joye和Quisquater以及DeJonge和Chaum还提出了一些额外的攻击。在整篇论文中,我们观察到通过在加密或签名之前正确填充消息可以防御许多攻击。
致谢
我要感谢Susan Landau鼓励我撰写调查问卷,感谢Tony Knapp帮忙编辑手稿。我还要感谢在早些时候Mihir Bellare、Igor Shparlinski和R. Venkatesan对草案发表的评论。
以上是 二十年以来对 RSA 密码系统攻击综述 的全部内容, 来源链接: utcz.com/p/199144.html