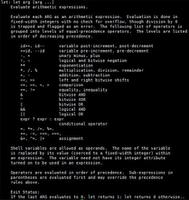
昨天微信的一道面试题，求解

  • Z时代
  • 2024-01-10
  • 分类：IT

题目是: 有A B C D 4个候选元素，2个元素展示位。写一个推荐程序，每一次选择2个不同的元素去展示。要求多次推荐后，A B C D推荐次数出现的比例趋近4:3:2:1。元素出现越随机越好。

注意是两个不同的元素。

回答：

P(X1 X2)为出现组合X1,X2的概率
则有：
P(AB) + P(AC) + P(AD) = 4/10
P(AB) + P(BC) + P(BD) = 3/10
P(AC) + P(BC) + P(CD) = 2/10
P(AD) + P(BD) + P(CD) = 1/10
且 0 <= P(x) <= 1
为了满足越随机越好可以以最小化方差为目标进行求解。

注：最小化方差时不是线性规划问题。可以考虑用如粒子群优化等算法来求解。

回答：

分别准备5个概率表，一个四抽一的概率表和四个三抽一的概率表。

四抽一的概率分别是4:3:2:1。
三抽一分四种情况：

  • 第一次抽到的是D，则剩下ABC，它们的概率为4:3:2

  • 第一次抽到的是C，则剩下ABD，它们的概率是4:3:1

  • 后面两个同理

抽取的时候分两次，第一次先从四抽一里面抽一个，第二次从对应的三抽一里面抽一个。

回答：

用 Excel 凑了个数字，方程不会解 @_@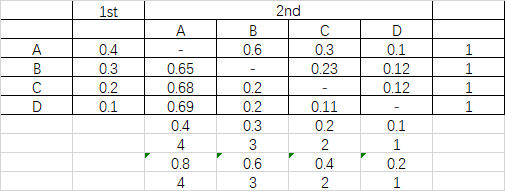
图片描述
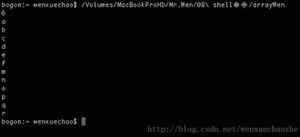
用程序跑了验证了一下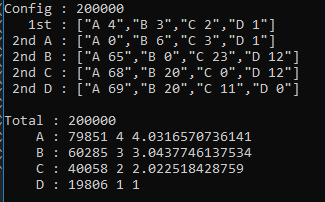
图片描述

以下回答，不正确

从抽一个元素开始，4:3:2:1 最简单的一种方案：

// 从以下数组随机抽取一个元素，概率就是 4:3:2:1
let pool = [A,A,A,A,B,B,B,C,C,D]

抽2个元素

// 抽第一个元素，抽取池如下
let pool = [A,A,A,A,B,B,B,C,C,D];
// 抽第二个元素
// 假设 第一个元素 item 抽出的是 A，那么剩下的 B:C:D 要 3:2:1，所以抽取池应该是 [B,B,B,C,C,D]
// 抽取的是其他元素类推
if(item === A)
    pool2 = [B,B,B,C,C,D]
else if(item === B)
    pool2 = [A,A,A,A,C,C,D]
else if(item === C)
    pool2 = [A,A,A,A,B,B,B,D]
else if(item === D)
    pool2 = [A,A,A,A,B,B,B,C,C]

以上是 昨天微信的一道面试题，求解 的全部内容， 来源链接： utcz.com/p/167959.html

回到顶部